Лабораторная работа 2 Анализ временных рядов Постановка задачи
 Скачать 27.19 Kb. Скачать 27.19 Kb.
|
|
Лабораторная работа № 2 Анализ временных рядов 1.Постановка задачи Временным рядом называется набор наблюдаемых значений какого-либо показателя y , которые фиксируются с некоторым постоянным шагом (через день, неделю, месяц, квартал, год). Такой набор полностью определен значениями показателя k y и номером k , соответствующим моменту времени k t его фиксации. Поэтому под временным рядом показателя будем понимать набор его значений k n y , y ,..., y ,..., y 1 2 в моменты времени k n t ,t ,...,t ,...,t 1 2 . Анализ временных рядов обычно предполагает решение двух задач. 1. Выявление тенденции изменения показателя во времени или, как говорят иначе, тренда. Эта задача сводится к нахождению относительно простой функции y f (t) , описывающей изменение показателя. В качестве такой функции обычно используются линейная, квадратичная или тригонометрическая функции. 2. Выполнение прогноза изменения анализируемого показателя во времени на период ( 1,2,3,...). Проиллюстрируем решение перечисленных задач на следующем примере. Пусть известен объем выпуска продукции по месяцам с января (1-й месяц) по май (5-й месяц), который задается табл. 2.1. В табл. 2.1 объем выпуска 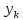 (тыс. шт.) в k -й месяц (тыс. шт.) в k -й месяц 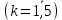 задается равенством: задается равенством: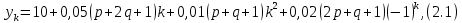 Используя данные (2.1) в табл. 2.1, определить: 1. Линейный тренд, описывающий изменение объема выпуска по месяцам в виде: 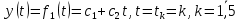 (2.2) (2.2)2. Квадратичный тренд, задаваемый равенством: 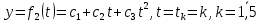 (2.3) (2.3)3. Погрешность приближения данных временным рядом при использовании трендов (2.2), (2.3). 4. Прогнозируемое значение объема выпуска в июне (6 месяц года). 2.Имитационная модель процесса Определение линейного тренда. Найдем коэффициенты 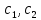 , задающие линейный тренд (2.2) методом наименьших квадратов (МНК), минимизируя отклонения между заданными значениями k y и полученными по формуле (2.2), то есть из условия: , задающие линейный тренд (2.2) методом наименьших квадратов (МНК), минимизируя отклонения между заданными значениями k y и полученными по формуле (2.2), то есть из условия: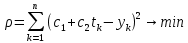 . .Согласно МНК получаем следующую СЛАУ относительно неизвестных 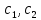 : :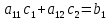 ; ; (2.4) 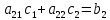 , ,где 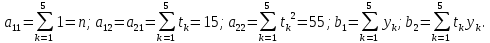 В результате решения СЛАУ (2.4) находятся значения 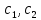 и линейный тренд (2.2). Определение квадратичного тренда. и линейный тренд (2.2). Определение квадратичного тренда. Для нахождения коэффициентов 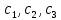 квадратичного тренда (2.3) МНК формируется СЛАУ вида: квадратичного тренда (2.3) МНК формируется СЛАУ вида: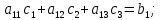 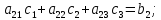 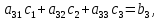 (2.5) где 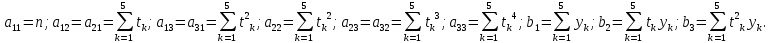 В результате решения СЛАУ (2.5) находятся неизвестные 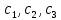 , затем с учетом равенства (2.3) квадратичный тренд. , затем с учетом равенства (2.3) квадратичный тренд.Для нахождения погрешности приближения временного ряда линейным трендом (2.2) сначала находится относительная погрешность в узлах 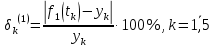 , (2.6) , (2.6)В качестве погрешности квадратичного приближения принимается наибольшее из значений (2.6). При квадратичном приближении (2.3) находится значение: 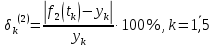 , (2.7) , (2.7)а затем среди полученных значений выбирается наибольшее, которое и принимается в качестве погрешности квадратичного приближения. Прогнозирование объема выпуска с использованием трендов (2.2), (2.3) в июне (шестой месяц) выполняется по формулам: 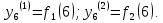 3. Ход работы Рассмотрим порядок выполнения работы для случая p 0 и q 8. Тогда объем выпуска продукции вычисляется по формуле (2.1): 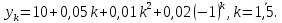 На листе Excel (рис. 2.1) сформируем расчетную область. Для построения табл. 2.1 с исходными данными выполняются следующие действия: 1) создаем автоматизированный список с номерами месяцев в ячейках В5:F5; 2) используя формулу (2.1), вычисляем объем выпуска продукции 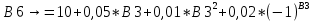 Формулу распространяем так, чтобы получить значение выпуска продукции для всех месяцев. Сначала найдем коэффициенты 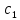 и и 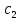 линейного тренда линейного тренда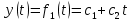 . Для их вычисления запишем систему уравнений (2.4) и, используя формулы для расчета ее коэффициентов, получаем: . Для их вычисления запишем систему уравнений (2.4) и, используя формулы для расчета ее коэффициентов, получаем: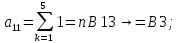 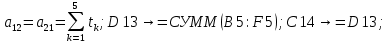 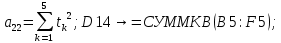 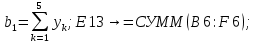 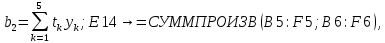 где функция СУММКВ(арг) подсчитывает сумму возведенных в квадрат аргументов. Решим систему методом Гаусса. Разделим первое уравнение на 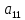 : :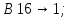 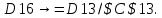 Формулу из ячейки D16 распространяем вправо на ячейку E17. Далее из второго уравнения вычтем первое, умноженное на  : : Формулу из ячейки D17 распространяем вправо на ячейку E17. Вычислим неизвестные: 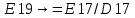 ; ;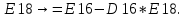 Теперь вычислим коэффициенты квадратичного тренда 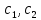 и и 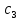 , используя систему (2.5). Для коэффициентов системы (2.5) понадобиться вычислять сумму , используя систему (2.5). Для коэффициентов системы (2.5) понадобиться вычислять сумму 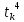 , поэтому сделаем вспомогательные вычисления. Добавим еще одну строку с заголовком «t_k^2» (рис. 2.1) и посчитаем для нее данные по формуле , поэтому сделаем вспомогательные вычисления. Добавим еще одну строку с заголовком «t_k^2» (рис. 2.1) и посчитаем для нее данные по формуле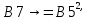 которую распространим вправо для всех пяти лет. Сформируем сначала матрицу системы (см. рис. 2.1): 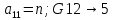 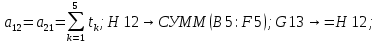 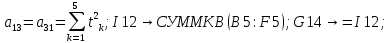 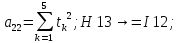  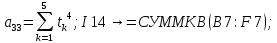 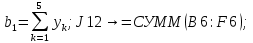 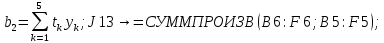 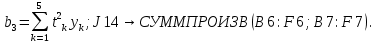 Решаем систему матричным методом: 1) F16 =МОБР(G16:I18), 2) выделяем диапазон G16:I18, размещаем курсор в строке формул и нажимаем одновременно Ctrl, Shift, Enter. Для определения коэффициентов 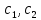 и и 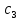 выполняем: выполняем: 1) I19 =МУМНОЖ(G16:I18;J12:J14); 2) выделяем диапазон I19:I21, размещаем курсор в строке формул и нажимаем одновременно Ctrl, Shift, Enter. Теперь сравним расчеты реального объема продукции по заданной формуле (2.1) и формулам (2.2) и (2.3). Для этого на листе Excel сформируем дополнительно еще одну таблицу (рис. 2.2), куда скопируем уже рассчитанный объем выпуска продукции по формулам (2.1) и вычислим объем продукции при использовании построенных трендов: В24 =В6; В25 =$E$18+$E$19*B23; В26 =$I$19+$I$20*B23+$I$21*B23^2. Полученные формулы распространим вправо, заполняя диапазон В24:F26. Вычислим погрешность по годам по формулам (2.6) и (2.7) соответственно для линейного тренда и квадратичного: В27 =ABS(B25-B24)/B24; В28 =ABS(B26-B24)/B24, где функция ABS(число) вычисляет модуль числа. Распространяем формулы вправо для вычисления погрешности для каждого месяца. Найдем погрешность вычисления: – для линейного тренда В29 =МАКС(B27:F27); – для квадратичного тренда В30 =МАКС(B28:F28). Сравнивая значения погрешностей, можно сделать вывод, что использование квадратичного тренда в данном случае лучше, так как погрешность вычислений для него меньше (0,0164 или 1,64 %). Выполним прогноз для шестого месяца. Добавим в строку «Месяц t_k» еще одно число (6 месяц), выделим ячейки G25:G26 и сместим формулы вправо, используя маркер автозаполнения. Из расчетов видно, что линейный тренд прогнозирует объем выпуска 10,298тыс. шт., а квадратичный 11,048тыс. шт. Студент 100502-ЗиСа-о20 Лущаков М. А. |
