Лабораторная работа по сопротивлению материалов. Лабораторная работа 2 Цель работы экспериментальное определение модуля упругости
 Скачать 221.5 Kb.
|
Цель работы: экспериментальное определение модуля упругости (модуля Юнга ) и коэффициента Пуассона стального образца. Приборы и оборудование: экспериментальная установка ОСМ-11 ЛР-09, штангенциркуль. Краткие сведения из теории Значения упругих характеристик могут быть получены только экспериментальным путём при испытании образцов на растяжение (сжатие), изгиб и кручение. Различают материалы изотропные и анизотропные. Изотропия означает независимость свойств материала от направления воздействия нагрузки. Изотропные материалы характеризуются тремя упругими постоянными: модулем Юнга, коэффициентом Пуассона и модулем сдвига. При этом, как показывает теория, только две из них являются линейно независимыми. Модуль Юнга или модуль упругости первого рода E характеризует сопротивляемость материала деформированию в направлении воздействия растягивающих или сжимающих нагрузок. Чем больше модуль Юнга, тем меньше удлинение или укорочение стержня при прочих равных условиях (длине, площади, нагрузке). Модуль Юнга является коэффициентом пропорциональности между нормальным напряжением  и относительной линейной деформацией  в законе Гука, записанном в дифференциальной форме:  . На основе этой формулы находят опытным путём значение модуля упругости ,где  формула для напряжения при растяжении, подтверждённая теорией упругости (эталоном точности для сопротивления материалов) и опытными данными; F – сила, растягивающая образец и определяемая по силоизмерительному устройству; A – площадь поперечного сечения, определяемая путём измерения размеров;  относительная продольная деформация, определяемая методом электрического тензометрирования.Коэффициент Пуассона  характеризует способность материала сопротивляться поперечному деформированию, т.е. изменению размеров в направлении, перпендикулярном воздействию силы. Это сопротивление французский академик Пуассон предложил характеризовать в безразмерной форме как модуль отношения поперечной  и продольной относительных деформаций, определяемых опытным путём: .Модуль сдвига или модуль упругости второго рода G характеризует сопротивляемость материала угловым деформациям при воздействии пары сил. Он является коэффициентом пропорциональности между касательным напряжением  и углом сдвига  в законе Гука при сдвиге, записанном в дифференциальной форме:  . На основе этой формулы можно экспериментально определить модуль сдвига, например, при кручении образца круглого сечения. В данной работе модуль сдвига определяют косвенным путём, исходя из теоретической зависимости между тремя упругими постоянными: .Упругие постоянные материала имеют более стабильные значения по сравнению с механическими характеристиками. Например, для различных марок сталей временное сопротивление может отличаться в несколько раз (от 400 до 4000 МПа и выше), в то время как среднестатистические значения упругих постоянных для всех марок сталей изменяются в узких пределах:  МПа;  ;  МПа.В лабораторной работе необходимо произвести сравнение полученных значений постоянных со средними справочными данными для стали:  МПа;  ;  МПа.На рис. 2.1 показан эскиз образца с наклеенными активными тензодатчиками. 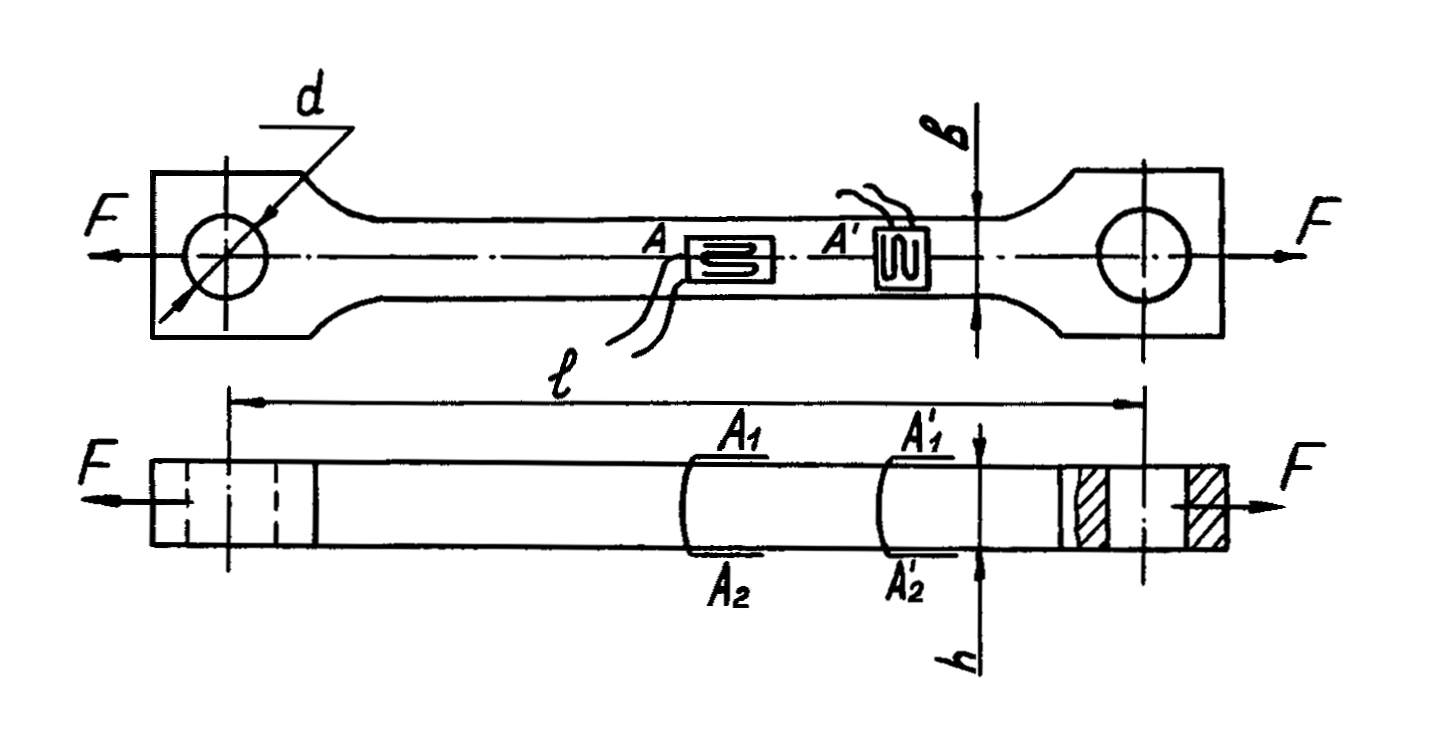 Рис. 2.1. Образец для определения упругих постоянных Этот образец подвергают нагружению, близкому к осевому растяжению, в пределах пропорциональности на гидравлической машине Р-10. Для измерения продольной относительной деформации служат активные датчики  и  , а для измерения поперечной относительной деформации  активные датчики  и  . Тензодатчики наклеены попарно на противоположных гранях плоского образца и соединены последовательно с той целью, чтобы исключить влияние изгибных деформаций, которые возникают вследствие нестрого осевого растяжения образца на испытательной машине.Экспериментальная часть измеряют штангенциркулем размеры bи h поперечного сечения образца в месте наклейки тензодатчиков; устанавливают образец в захватах испытательной машины и создают небольшое натяжение; включают тензостанцию для прогрева в течение 10 мин; нагружают образец условно нулевой силой  кгс, берут первоначальные отсчёты  ,  по каждому из датчиков и записывают их в протокол испытания (табл. 2);дают приращение нагрузки  кгс, берут соответствующие отсчёты  ,  и записывают их в протокол испытания;разгружают образец до нулевой нагрузки; находят разность показаний тензодатчиков:  ;  ;находят относительные продольную и поперечную деформации, соответствующие приращению нагрузки кгс: ;  ;вычисляют площадь сечения и нормальное напряжение, возникающее от приращения нагрузки  Н: ;  ;определяют опытное значение модуля Юнга ;определяют опытное значение коэффициента Пуассона  ;вычисляют косвенное значение модуля сдвига ;производят сравнение полученных значений упругих постоянных со средними справочными значениями для стали:  ;  ;  ;делают выводы по работе.
Таблица 2 Протокол испытания образца на растяжение 1) TFначальн= 69 К TFконечн= 1030 К ∆T= 1030-69= 961 К ∆T= TFконечн – TFначальн ∆T1= T’Fконечн – T’Fначальн ∆T1= -292+27= -265 К 2) ε= ∆Tср*10-6= 961*10-6 ε’= ∆T’ср*10-6= (-265)*10-6 b=3,5*10-3м h= 40*10-3м ∆F= 2500Н 3) A= bh= 3,5*10-3 * 40*10-3 мм2 δ=∆F/A= 2500/(3,5*10-3 * 40*10-3) Н/м 4) E= δ/ε= 2500/(3,5*10-3 * 40*10-3 * 961*10-6)= 1,85 *1011 Па 5) µ=lε’/εl = 2,65*10-6/(961*10-8)= 0,28 6) G= F/(2*(1+µ))= 1,85*1011/(2*(1+0,28))= 7,23*1010 Пр 7) δ(E)= (1,85 *1011- 2*1015)/(2*1011)= 0,075=7,5% δ(µ)= (0,28-0,3)/(8*1020)= 0,067=6,7% δ(E)= (7,23*1010- 8*1010)/(8*1010)= 0,096=9,6% Вывод: В ходе лабораторной работы были экспериментально определены модуль упругости (модуль Юнга E= 1,85*1011Па) и коэффициент Пуассона (µ= 0,28) и модуль сдвига (G= 7,23*1010) стального образца.
| ||||||||||||||||||||||||||||||||
, кгс
