Механические свойства костной ткани. Механические свойства костной ткани. Определение модуля упругости кости по изгибу

• Название: Механические свойства костной ткани. Определение модуля упругости кости по изгибу
• Анкор: Механические свойства костной ткани.doc
• Дата: 17.12.2017
• Размер: 465 Kb.
• Имя файла: Механические свойства костной ткани.doc
• Тип: Документы; #11941
• Категория: Физика

Механические свойства костной ткани. Определение модуля упругости кости по изгибу

Цель работы: изучить физические основы воздействия на биологические ткани механических нагрузок и биомеханические свойства костной ткани в связи с особенностями ее структурной организации. Освоить один из методов определения модуля упругости (модуля Юнга) кости.
Важность изучения и понимания механических свойств биологических тканей обусловлена:

1) потребностью совершенствования средств защиты человека от неблагоприятных силовых воздействий, методов лечения травм, задачей протезирования органов и тканей;

2) необходимостью создания новых высокопрочных материалов близких к часто технологически более совершенным биотканям;

3) необходимостью изучения механизмов, обуславливающих процессы роста и развития биологических тканей.

Биологические ткани принято разделять на жидкости (кровь и лимфа), мягкие ткани (эпителий, хрящевые и мышечные ткани) и твердые ткани (кость). В данной работе рассматриваются, главным образом, механические свойства костной ткани.

1.Физические основы воздействия на ткани механических нагрузок

Определим содержание основных понятий и величин, которые обычно используются для характеристики механических свойств различных сред, в том числе, биотканей и которые будут необходимы для понимания следующего ниже материала.



Механические свойства тел проявляются в их реакции на внешние силы (нагрузки). Изменения формы и/или размеров образца из соответствующего материала под действием внешних сил называют деформацией.

Различают упругие и пластические деформации. Упругость определяют как способность деформируемого тела восстанавливать исходные размеры после снятия нагрузки; пластичность - как способность получать остаточные деформации без разрушения и сохранять их после снятия нагрузки.

На рис.1 показаны основные виды деформации твердых тел. Направления внешних сил указано стрелками. Пунктир соответствует деформированному образцу.

В теле человека внешние силы чаще всего вызывают сжатие, растяжение и изгиб соответствующих элементов.

Мерой деформации является относительная деформация, равная отношению абсолютной деформации к величине, характеризующей первоначальные размеры или форму образца. Например, для одноосного растяжения (сжатия) (см. рис.1.,b,c) относительная деформация = l/l, где l-начальная длина образца, l — абсолютная деформация;  - величина безразмерная.

Обычно на тела действуют сосредоточенные в точке или распределенные по определенной поверхности силы (нагрузки). Различают также статические и динамические нагрузки. Статические нагружают тело медленно и затем не изменяют своей величины с течением времени. Примерами динамических нагрузок являются ударные и повторно-переменные (циклические) нагрузки.

Механическое напряжение - величина, которая характеризует внутренние силы, возникающие в образце при деформации. Эти силы противодействуют внешним силам, которые вызывают деформацию.

Напряжение определяется значением внешней силы, приходящейся на единицу площади сечения образца, и обозначается буквами  ( при растяжении или сжатии),  при сдвиге); его размерность в СИ - Н/м² (Па).

Модуль упругости (модуль Юнга) Е - отношение напряжения к относительному удлинению (сжатию), характеризует способность материала, из которого сделан деформируемый образец, сопротивляться упругой деформации растяжения(сжатия); размерность в СИ - Н/м² . Рассматривают также модуль сдвига G при деформации сдвига и коэффициент Пуассона . Последний характеризует относительное изменение объема тела при упругой деформации. Если =0,5, то материал из которого сделано деформируемое тело, называется несжимаемым.

Прочность деформируемого тела - способность тела сопротивляться разрушению при действии внешних сил. При исследовании прочности используют предел прочности материала - напряжение в материале при различных видах деформации, соответствующее максимальному (до разрушения образца) значению нагрузки, или разрушающее напряжение - отношение нагрузки, необходимой для полного разрушения образца, к его поперечному сечению в месте разрушения.

Выделим присущие большинству биологических тканей общие черты в механическом поведении.

1) Большинство этих тканей анизотропно, т.е. их физические, в том числе и механические свойства в различных направлениях различны. Анизотропия биотканей связана, прежде всего, с определенным порядком в расположении строящих ее структурных элементов.

2) Почти все биоткани обнаруживают при деформировании характерные временные эффекты: а) при фиксированной деформации происходит релаксация (спад) напряжения; б) при фиксированной нагрузке (напряжении) рост деформации во времени; данное явление иногда называют течением материала, чаще ползучестью или крипом; в) при циклическом нагружении колебания напряжений и деформаций различаются по фазе; г) механические характеристики тканей часто зависят от скорости деформации.

3)Зависимостям напряжения от деформации при нагрузке и разгрузке соответствуют разные кривые, формируется так называемая "петля гистерезиса".

Перечисленные в пунктах 2 и 3 факты являются проявлением вязкоупругого поведения биоткани.

Остановимся на содержании понятия "вязкоупругость" несколько подробнее. Можно представить себе два результата воздействия на материал внешних сил, при котором они совершают работу по его деформированию. Во-первых, работа внешних сил может запасаться в единице объема среды в виде потенциальной энергии деформации, обычно называемой объемной плотностью упругой энергии W (удельной энергией упругой деформации). Во-вторых, работа внешних сил может необратимо рассеиваться (диссипировать), расходуясь на преодоление сил внутреннего трения и переходя в тепло. Этот процесс характеризуется интенсивностью диссипации D в единице объема среды в единицу времени. Если при деформации W  0, а D = 0, среда называется упругой , при деформировании такой среды диссипация внешней работы отсутствует, и вся запасенная энергия при разгрузке тела переходит в работу по восстановлению формы и размеров образца. Если же W = 0, D  0, среда называется вязкой, при ее деформировании вся внешняя работа диссипирует (превращается в тепло). После снятия нагрузки вязкая среда остается в том же состоянии, в котором она была в момент снятия нагрузки. Все деформации в вязкой среде необратимы. Наконец, если W  0 и D  0, среда называется вязкоупругой. При ее деформировании какая-то часть внешней работы диссипирует (т.е. необратимо рассеивается в виде тепла), а остальная запасается в материале в виде энергии упругой деформации. После прекращения действия внешних сил в такой среде происходит упругое восстановление и одновременно с этим диссипация накопленной в ней энергии. Это и приводит к образованию петли гистерезиса, о которой упоминалось раньше. Таков общий подход к описанию многих механических свойств реальных, в том числе биологических сред.

Одна из главных задач механики деформируемых сред - установление связей между механическими напряжениями, деформациями и скоростями деформации. Рассмотрим несколько примеров:

а) идеально упругое изотропное тело Гука, W0, D = 0. В этом случае для одноосного растяжения (сжатия, см.рис.1 b,с)

 = Е  (закон Гука для этих видов деформации) (1)

Для деформации сдвига имеет вид:

 = G  , (2)

 - угол сдвига, мера деформации сдвига (рис.1,е), , - коэффициент Пуассона.

б) ньютоновская вязкая жидкость. Здесь W=0, D  0 и возникающее в текущей жидкости напряжение  связано с градиентом скорости (скоростью сдвига) следующим образом

 = , (3)

 - коэффициент динамической вязкости, характеристика текущей жидкости.

в) простейшее вязкоупругое твердое тело (тело Кельвина), приближенный анализ явления ползучести. Напомним, что в данном случае W  0, D  0.

Рассмотрим одну из возможных комбинаций упругости и вязкости. При суммировании напряжений тела Гука и ньютоновской вязкой жидкости получим следующее уравнение:

 = G  + , или  = G  +  (t - время). (4)

Пусть в теле, которому соответствует уравнение (4) в момент времени t=0 возникает напряжение  = ₀, которое затем поддерживается постоянным. Тогда решение (4), которое приводится без вывода, имеет вид:

, (5)

где  = /G. Этот параметр имеет размерность времени, называется временем запаздывания и характеризует запаздывание реакции материала (деформации) на приложенную нагрузку: развитие упругой деформации тормозится вязкостью среды.

После снятия внешней нагрузки происходит упругое восстановление тела, которое описывается формулой:

. (6)

Для той же среды можно показать, что 1) при циклическом нагружении возникает разность фаз между напряжением и деформацией, возрастающая с увеличением частоты внешнего воздействия и времени запаздывания; 2) отклик среды на внешнее воздействие зависит от скорости ее деформирования.

2. Механические свойства костной ткани

Несмотря на существование различных типов костей в теле человека и животных (это длинные трубчатые кости конечностей, плоские кости черепа, короткие кости - позвонки), для всех них характерны общие черты, которые далее будут рассмотрены, главным образом, на примере компактной и частично губчатой (спонгиозной) тканей трубчатых костей,

Напомним, что костная ткань один из видов соединительной ткани, состоящей из трех видов клеток и обизвествленного межклеточного матрикса.

Клетки составляют  1-2% от всего объема костной ткани, остальной объем занят порами и каналами (для компактной костной ткани пористость составляет 13-18%, для губчатой она выше) и твердой фазой - органическими и минеральными составляющими костных пластинок.

Органическая составляющая (40-50% твердой фазы) представлена коллагеном. Минеральная составляющая (50-60% твердой фазы) - преимущественно кристаллы гидроксилапатита Са₁₀ (РО₄ ) ₆ (ОН)₂ и других солей кальция.

В пределах пластинки коллаген - минеральные волокна ориентированы в определенном направлении и соединены связующим веществом.

Механические свойства кости определяются главным образом, составом твердой фазы и свойствами ее компонент. В экспериментах можно практически полностью удалить из кости органическую или минеральную составляющую. Форма и размеры образца при этом не меняются, но механические свойства будут разительно отличаться от свойств нормальной кости. Так, кость, лишенная органических веществ, необычайно хрупка, а деминерализованная кость приобретает резиноподобные свойства. Это означает, что костная ткань является прочным конструкционным композитным материалом лишь при определенном сочетании входящих в нее компонентов.

В статических условиях модули упругости коллагена и гидроксилапатита составляют Е_с 10⁹ Н/м² и Е_h 10¹¹ Н/м², соответственно, для компактной ткани кости Е 10¹⁰ Н/м² (для сравнения Е стали  210¹⁰ Н/м² , Е титана  10¹¹ Н/м² ). Полагают, что хотя гидроксилапатит и не соединен жестко с коллагеновыми волокнами, он все-таки существенно ограничивает перемещения и деформации последних. Таблица 1 иллюстрирует некоторые механические свойства костей, отличающихся содержанием минерального компонента.

Таблица.1.

Тип кости	Предел прочности при изгибе (МПа)	Е (ГПа)	Содержание минеральных компонентов,%	Плотность , кг/м3
Бедренная кость коровы	247	13,5	66,7	2060
Стенка среднего уха кита	33	31,3	86,4	2470

2.1. Компактное вещество костной ткани

При различных видах деформации компактное вещество костной ткани,

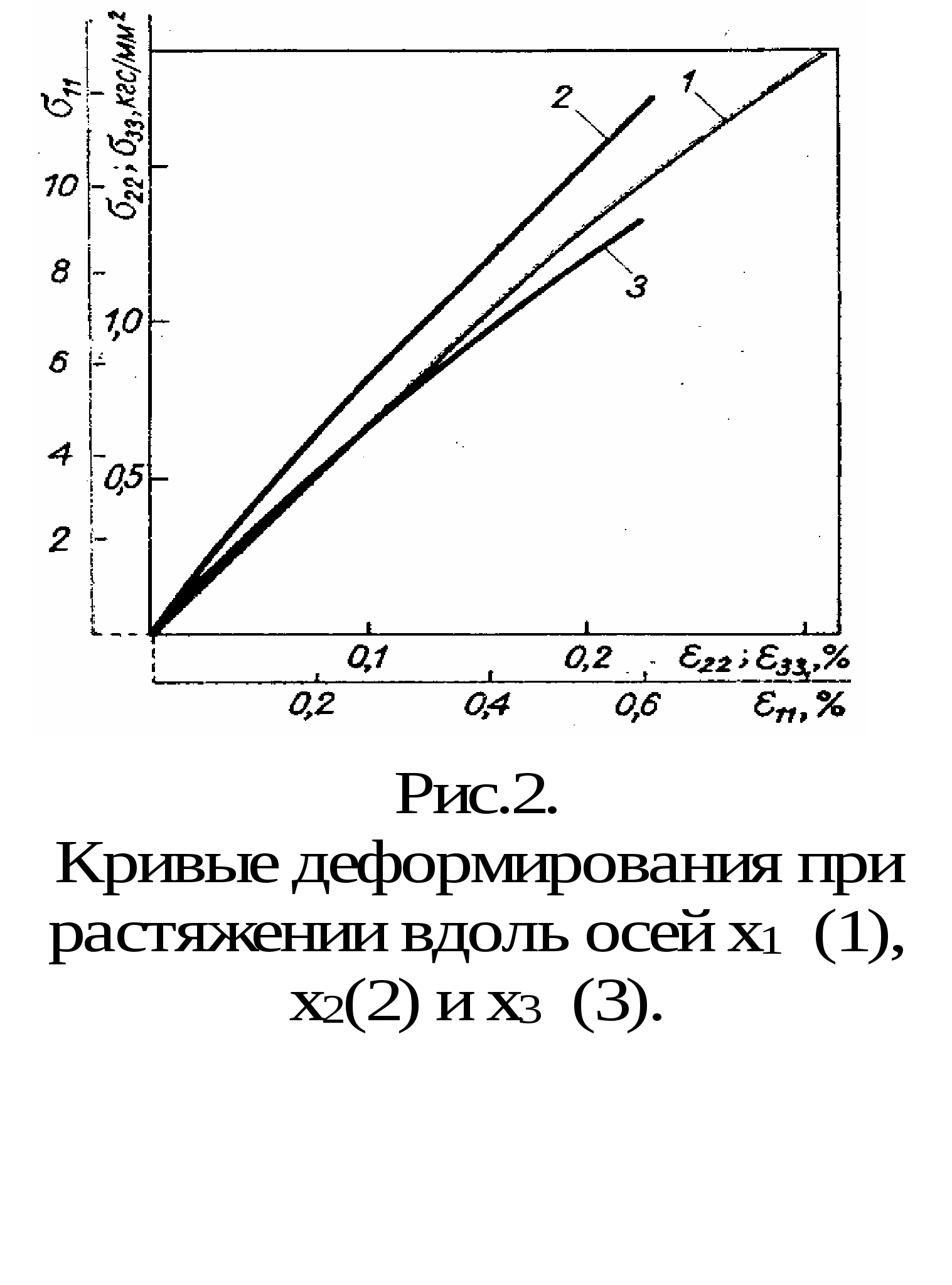
формирующее среднюю часть трубчатых костей, характеризуется нелинейной зависимостью напряжение-деформация и анизотропией упругих и прочностных свойств. Анизотропия проявляется существенной зависимостью этих свойств от направления нагружения, нелинейность - понижением модуля упругости материала с повышением уровня напряжения, опыты обычно проводятся при статическом нагружении. Для определения свойств кости как анизотропной среды вводится координатная система ось х₁, которая совмещается с направлением продольной оси кости, а х₂ и х₃ - с касательным и радиальным направлениями в плоскости, перпендикулярной х₁ . На рис.2 даны кривые деформирования образца воздушно-сухой компактной костной ткани большеберцовой кости человека при растяжении вдоль осей х₁ (кривая 1), х₂ (2), х₃ (3). Видно, что кривые 1, 2, 3 не совпадают.

Приведем значение средних (почему средних, показано ниже) по поперечному сечению большеберцовой кости взрослого человека модулей упругости для выбранных направлений, характеризующих анизотропию ткани:Е₁=18,35ГПа, Е₂ =8,5 ГПа, Е₃ =6,9 ГПа. Эти значения соответствуют линейной части графиков подобных показанным на рис.2. Вдоль продольной оси модуль упругости выше, чем в поперечных направлениях примерно в 2 раза, различие в Е₂ и Е₃ невелико.

Модули сдвига примерно в 3-4 раза меньше модулей упругости, но они так же различны, коэффициенты Пуассона лежат в диапазоне 0,4-0,2.

Анизотропия разрушающих напряжений больше проявляется при растяжении, чем при сжатии или кручении.

Очевидно, что в масштабах одной костной пластинки анизотропия механических свойств обусловлена ориентацией коллаген-минеральных волокон. Макроскопические образцы кости анизотропны из-за упорядоченного расположения остеонов и других структур этого уровня.

Значение разрушающих напряжений при сжатии значительно выше, чем при растяжении или кручении. Например, для образцов большеберцовой кости, вырезанных вдоль продольной оси, они составляют в среднем 200 МПа при сжатии вдоль оси, 12О МПа - при растяжении, 90 МПа - при кручении. Эти цифры иллюстрируют известное врачам-ортопедам положение: сжатие - менее опасный вид нагружения, чем растяжение и кручение.



Распределение всех характеристик упругих и прочностных свойств по отдельным зонам поперечного сечения кости неоднородно (отсюда их средние значения), причем по зонам меняются не только их абсолютные величины, но и соотношение с другими параметрами. Для модулей упругости это иллюстрируется рис.3.

Указанную неоднородность, прежде всего, необходимо учитывать при подборе заменителей костной ткани для обеспечения их механической совместимости с естественной тканью.



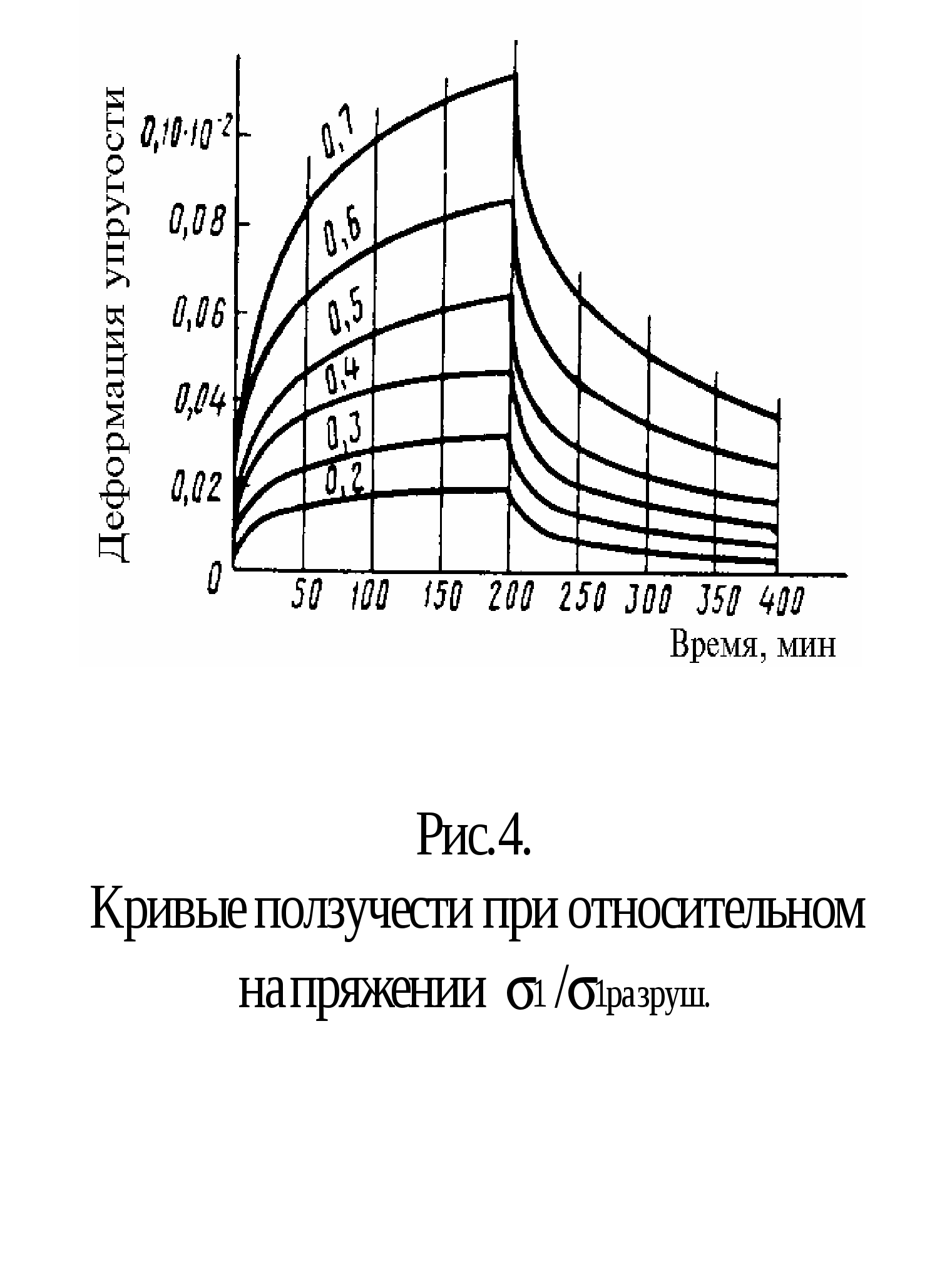
Вязкоупругое поведение костной ткани четко проявляется в зависимости ее механических характеристик от скорости деформации. Так, например, при сжатии вдоль продольной оси компактного вещества костной ткани человека модуль упругости меняется от 15,1 ГПа

при скорости деформации 0,001 с^-1 до 29,6 ГПа при скорости деформации 300 с^-1. Для компактного вещества кости экспериментально фиксируется явление ползучести с последующим восстановлением после разгрузки (рис.4). Причем при малых уровнях напряжения (₁/_{1 разруш.},  0,3, на рис.4 указаны значения этих отношений) деформация после разгрузки полностью исчезает, при более высоких значениях ₁ /_{1разруш.} имеют место небольшие остаточные деформации.

После достижения некоторого уровня напряжения в плоскости ,  образуется гистерезисная петля.

Отмеченные временные эффекты в кости, видимо, связаны с собственными вязкоупругими свойствами полимерных молекул коллагена, с неупругостью межклеточного матрикса и с наличием вязкой жидкости в костных канальцах.

Механические свойства компактной костной ткани человека изменяются с возрастом. В детском и юношеском возрасте, когда продолжается рост костей, модули упругости и сдвига, а также разрушающие напряжения костной ткани возрастают, а после достижения 20-25-летнего возраста эти показатели начинают постепенно понижаться. Разрушающие деформации меняются иначе - максимум у новорожденных, затем резкое понижение этих показателей (до 20-25 лет), и далее плавное понижение.

При длительных циклических испытаниях важнейшей характеристикой любого материала является усталостная долговечность, которая определяется количеством циклов нагружения ткани до разрушения материала. Приведенные ниже данные относятся к деформации изгиба компактной костной ткани бедренной кости быка. Было установлено, что повышение уровня напряжения приводит к нелинейному понижению усталостной долговечности независимо от частоты нагружения. При равном уровне напряжения увеличение частоты нагружения выше 30 Гц приводит к некоторому росту долговечности, при частотах меньше 30 Гц этот параметр остается практически постоянным.

2.2. Губчатое (спонгиозное) вещество костной ткани. Эта ткань в основном образует позвонки и концевые отделы трубчатых костей. Она составляет, примерно, 20% общей массы скелета взрослого человека, и ее строение зависит от функционального назначения кости.

Приводимые ниже данные относятся к наиболее исследованной спонгиозной костной ткани трубчатых костей.

Из технической статики известно, что максимально облегченная, но достаточно прочная структура должна представлять собой решетчатую конструкцию из стержней, следующих траекториям действия напряжений. Уже давно было обнаружено, что траектории растягивающих и сжимающих напряжений в кости находят отражение в ее губчатой структуре,т.е. в расположении костных балочек (трабекул). При анализе траекторий по которым расположены трабекулы в системе функционально взаимосвязанных костей, оказывается, что кривые продолжаются с одной кости на другую через суставы. Причем эта ситуация не запрограммирована генетически, а возникает как ответ на нагружение скелета в процессе морфогенеза.

По разным литературным источникам значения модуля упругости влажной спонгиозной ткани варьируются от 26 до 600 МПа, но они всегда ниже этих показателей для компактной ткани. Для головки бедренной кости разрушающие напряжения при сжатии составляют 3,7 - 11,4 МПа Такой разброс цифр, по-видимому, связан с сильной зависимостью этих величин от локализации исследуемого образца в кости и от направления нагружения относительно системы трабекул.

Характерно, что у лиц пожилого и старческого возрастов, которые в прошлом занимались тяжелым физическим трудом, значение разрушающего напряжения спонгиозной ткани несколько ниже, чем у людей умственного труда. У более молодых людей (25-40 лет) имеет место обратное явление. Очевидно, наличие длительных перегрузок выше физиологического уровня, вызывает с увеличением возраста необратимые изменения структуры и, следовательно, понижение сопротивляемости разрушению.

3. Определения модуля упругости костной ткани по изгибу

Установка для определения модуля упругости по деформации изгиба показана на рис.5. Край образца закрепляется на штативе с помощью зажимного винта. На противоположном краю имеется крюк для подвешивания грузов. Мерой деформации изгиба служит стрела прогиба, т.е. наибольшее отклонение одной из точек образца от первоначального положения. Стрела прогиба измеряется с помощью индикатора длин. Для модуля упругости образца в виде пластины из костной ткани теория дает следующее выражение :

, (7)

где Р - нагрузка; l - длина образца (расстояние между зажимным винтом и крюком); f - стрела изгиба; b - ширина образца; h - его высота.

Расстояние между зажимным винтом и крюком измеряют миллиметровой линейкой, линейные размеры штангенциркулем. Измерения делают в нескольких местах образца и берут их средние значения. Все размеры выражают в метрах, нагрузку Р - в ньютонах.

3.1. Исследование зависимости стрелы прогиба от нагрузки f(P).

Образец закрепляют на штативе в соответсвии с рис.5. Вертикальный стержень идикатора длин приводят в соприкосновение с верхней поверхностью образца в точке фиксации нагрузочного крюка. После этого стрелку индикатора устанавливают в нулевое положение. Постепенно, без толчков, нагружают образец, навешивая грузы (Р) на крюк. При этом для каждой нагрузки отмечают стрелу прогиба (f) по индикатору длин. Результаты измерений, выраженные в системе СИ заносят в таблицу.

Р, н (ньютон)
f, м (метр)

По данным таблицы строят график зависимости стрелы прогиба от нагрузки, откладывая по оси х нагрузку, а по оси y стрелу прогиба.

3.2. Определение модуля упругости кости

В формулу (7) подставляют средние значения размеров образца, вместо Р - сумму всех нагрузок, вместо f - сумму всех стрел прогиба, что равносильно нахождению их средних значений и вычисляют Е.

Контрольные вопросы:

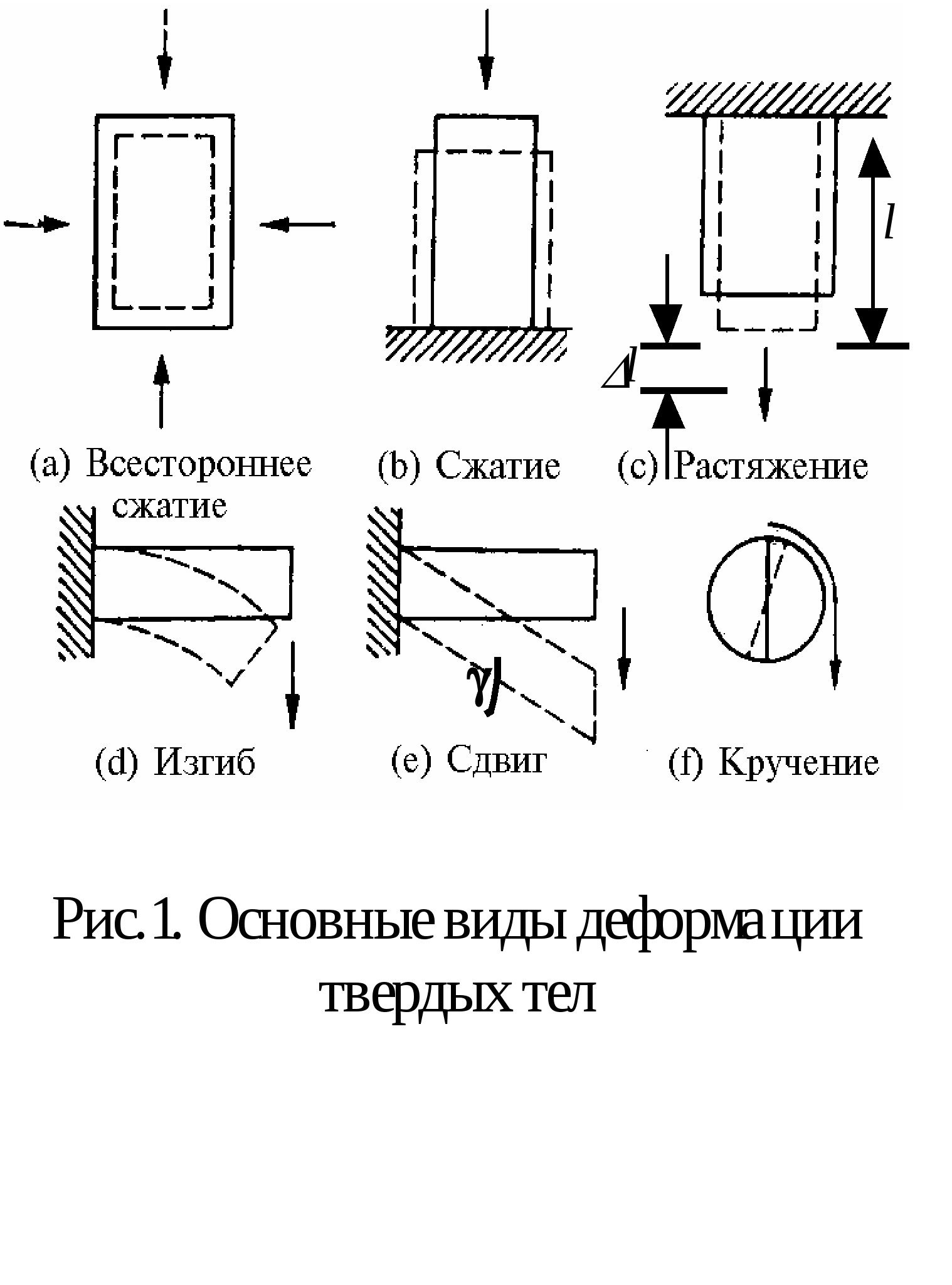
1. Дайте определение деформации. Перечислите основные виды деформации твердых тел. Какие из них чаще реализуются в теле человека под действием внешних сил?.

2. Дайте определение механического напряжения.

3. Каков физический смысл модулей упругости, коэффициент Пуассона?

4. Дайте определение прочности деформируемого тела, предела прочности.

5. Что такое анизотропия биотканей, какова ее природа?

6. Перечислите основные факты, которые определяют вязкоупругое поведение биоткани.

7. Охарактеризуйте механическое поведение костной ткани.

8. Опишите методику определения модуля упругости кости, приведенную в данной работе.

Литература:

1. Проблемы прочности в биомеханике, под.ред, И.Ф.Образцова, М., 1988.

2. С.А.Регирер. Лекции по биологической механике, М., 1980.

3. Р.Глазер. Очерк основ биомеханики, М., 1988.

4. А.Н.Ремизов. Медицинская и биологическая физика, М., 1987 или 1996.

5. И.В.Кнетс, Г.О.Пфафрод, Ю.Ж.Саулгозис, Деформирование и разрушение твердых биологических тканей, Рига, 1980.

6. J.B.Park, Biomaterials science and engineering, N. Y, 1984.

7. Ф.К.Горский, Н.М.Сакевич. Физический практикум с элементами электроники, Мн.1980, лаб.раб.№ 4.

8. И.А.Эссаулова и др. Руководство к лабораторным работам по медицинской и биологической физике, М. 1987, лаб.раб. № 17.