отчет. отчет 1 Абрамов. Лабораторная работа 2 Численные методы решения нелинейных уравнений и систем студент 3го курса группы 19саи
 Скачать 2.27 Mb. Скачать 2.27 Mb.
|
|
МИНОБРНАУКИ РОССИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Нижегородский государственный технический университет им. Р.Е. Алексеева» (НГТУ) Кафедра: «Цифровая экономика» Дисциплина: «Численные методы» Лабораторная работа №2 «Численные методы решения нелинейных уравнений и систем» Выполнил: студент 3-го курса группы 19-САИ Абрамов Павел Витальевич Проверил: д.ф.м.н., проф. Катаева Лилия Юрьевна Нижний Новгород, 2021 ОглавлениеПостановка задач 3 Методы решения 4 Ручной счёт 8 Проверка вычислений 17 •Mathcad 17 •Excel 25 •C++ 35 Заключение, выводы, погрешность, оценка 42 Литература 43 Постановка задачЗадание №1. Используя метод итераций, вычислить систему нелинейных уравнений. 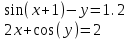  Задание №2. Используя метод Ньютона, вычислить систему нелинейных уравнений. 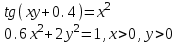 Задание №3. Используя графический метод, вычислить нелинейное уравнение средством Mathcad 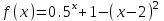 Задание №4. Используя метод половинного деления, вычислить нелинейное уравнение 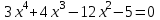 Задание №5. Используя метод хорд, вычислить нелинейное уравнение 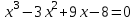 Задание №6. Используя комбинированный метод, вычислить нелинейное уравнение 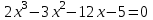 Задание №7. Используя метод простых итераций, вычислить нелинейное уравнение 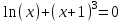 Методы решенияМетод итераций. Одним из наиболее важных способов численного решения нелинейных уравнений является метод итерации (последовательных приближений). Пусть дано уравнение: 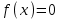 , где , где 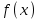 - непрерывная функция. Найдём корни уравнения, заменив данное уравнение ему равносильным: - непрерывная функция. Найдём корни уравнения, заменив данное уравнение ему равносильным: 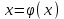 . Затем, выберем грубое приближение . Затем, выберем грубое приближение 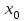 , и подставим его в правую часть нового уравнения, , и подставим его в правую часть нового уравнения,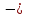 получим число получим число 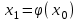 . (1) Данный процесс будем повторять . (1) Данный процесс будем повторять 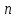 - ое кол-во раз: - ое кол-во раз: 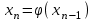 . (2) . (2)Если последовательность будет сходиться, то есть, будет существовать такой предел 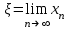 , то, переходя к пределу в равенстве и предполагая функцию , то, переходя к пределу в равенстве и предполагая функцию 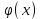 непрерывной, найдем непрерывной, найдем 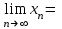 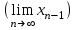 или или 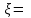 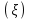 . Таким образом, предел . Таким образом, предел 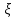 является корнем уравнения и может быть вычислен по формуле является корнем уравнения и может быть вычислен по формуле 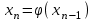 с любой точностью. с любой точностью.Метод Ньютона (касательных). Одним из продвинутых методов вычисления системы нелинейных уравнений является ‘Метод Ньютона’. Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить ноль первой производной либо градиента в случае многомерного пространства. Для начала, следует записать функцию в итерационном виде, перенеся все её аргументы влево. Затем, выберем корень для уточнения, на графике параллельно выбрав приближенный интервал значений координат. После чего, зададим приближение 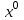 и точность вычислений и точность вычислений 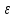 . .Формула итерационного процесса: 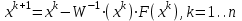 (1), (1),где  матрица Якобиана (матрица производных аргументов функций), а матрица Якобиана (матрица производных аргументов функций), а 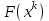 - левая часть уравнений. - левая часть уравнений. Если 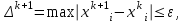 тогда считаем тогда считаем 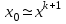 , иначе, продолжаем итерационный процесс. , иначе, продолжаем итерационный процесс.Данный алгоритм также действует на системы нелинейных уравнений, где присутствуют аргументы помимо ‘x’. Графический метод. Графический метод используется для агрегирования данных на этапе их первичного анализа. График показывает соотношение данных с помощью геометрических образов и изобразительных средств и позволяет представить данные в графическо (наглядном) виде. В начале, задается система уравнений, записывающаяся впоследствии в более удобном виде (коэффициенты переносятся в одну сторону) для анализа и вычислений. После чего, система отображается графически, что позволяет наглядно определить интервалы нахождения корней, если таковые имеются. Если корни имеются, то, в нашем случае, используем блок (Given-root), для точного уточнения и поиска. Если нет, то система не имеет решения. Метод половинного деления. Метод деления пополам позволяет исключать в точности половину интервала на каждой итерации. При использовании метода считается, что функция непрерывна и имеет на концах интервала разный знак. После вычисления значения функции в середине интервала одна часть интервала отбрасывается так, чтобы функция имела разный знак на концах оставшейся части. Итерации метода деления пополам прекращаются, если интервал становится достаточно малым. Алгоритм: Найти отрезок  такой, что такой, что 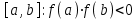 Введем половинный коэффициент 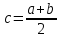 Если выполняется условие, что 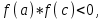 то то 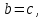 иначе иначе 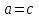 Продолжая процесс половинного деления, получим малый отрезок  , содержащий корень уравнения , содержащий корень уравненияМетод хорд. Пусть задана функция f(x) действительного переменного. Требуется найти корни уравнения f(x)=0. (1) Задача нахождения корней уравнения (1) обычно решается в 2 этапа. На первом этапе проводится отделение корней, то есть выделение отрезков, содержащих только один корень. На втором этапе, используя начальное приближение, строится итерационный процесс, позволяющий уточнить значение отыскиваемого корня Проводится хорда через точки a, b, где уравнение хорды:  В точке 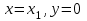 , в результате получим первое приближение корня , в результате получим первое приближение корня 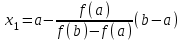 (2) (2)Затем, проверим два условия: 1. 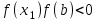 ; 2. ; 2. 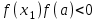 Если выполняется 1., то в (2) заменим ‘a’ на 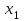 , получив , получив 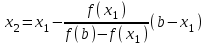 . После чего, продолжая процесс, получим формулу нахождения n-ого приближения . После чего, продолжая процесс, получим формулу нахождения n-ого приближения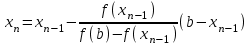 Если выполняется 2., то в (2) заменим ‘b’ на 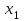 , получив , получив 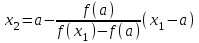 . После чего, продолжая процесс, получим формулу нахождения n-ого приближения . После чего, продолжая процесс, получим формулу нахождения n-ого приближения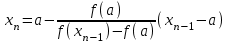 Точкой останова будет являться неравенство: 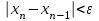 Комбинированный метод. Комбинируя метод хорд и метод Ньютона, можно построить метод отыскания вещественных корней уравнения, 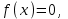 в котором при прежних предположениях относительно в котором при прежних предположениях относительно 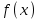 на каждом шаге итерационного процесса мы получаем два приближения к корню на каждом шаге итерационного процесса мы получаем два приближения к корню 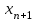 и и 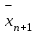 причем причем 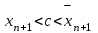 , где , где 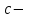 значение корня. значение корня.Пусть известен отрезок  , который содержит один корень уравнения , который содержит один корень уравнения 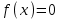 . Функция . Функция 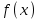 является дважды непрерывно дифференцируемой на отрезке является дважды непрерывно дифференцируемой на отрезке  . Функция принимает на концах отрезка значениях разных знаков . Функция принимает на концах отрезка значениях разных знаков 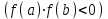 . .Первая и вторая производные не обращаются в ноль на отрезке. Возможны два случая: Если 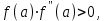 тогда слева применяется метод Ньютона, а справа метод хорд. Формулы метода: тогда слева применяется метод Ньютона, а справа метод хорд. Формулы метода: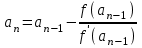 и и 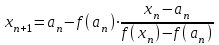 Если 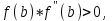 тогда слева применяется метод хорд, а справа метод Ньютона. Формулы метода: тогда слева применяется метод хорд, а справа метод Ньютона. Формулы метода: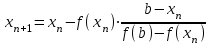 и и 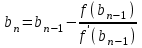 Точкой останова будет неравенство: 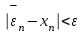 , где , где 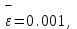 а а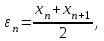 Ручной счётРучной счёт Методом итераций 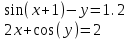 Итерационный вид Приближение, исходя из интервала 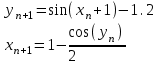 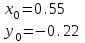 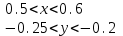 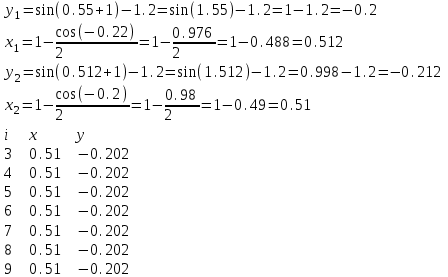 Ручной счёт Методом Ньютона 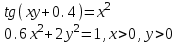 Приведем к виду: 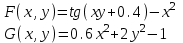 , выберем приближение , выберем приближение 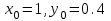 Матрица Якобиана: 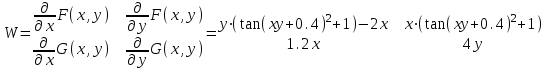 Обратная матрица Якобиана: 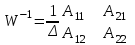 Определитель: 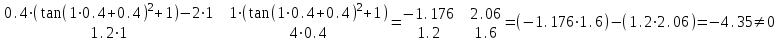 Транспонированная матрица: 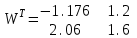 Алгебраические дополнения: 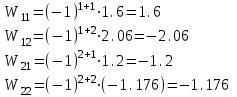 Обратная матрица (Итог): 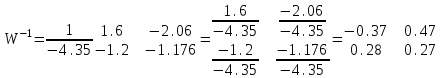 Левая часть уравнений: 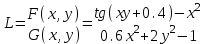 N = 0  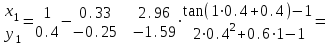 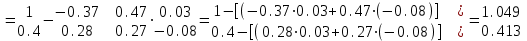  Ручной счёт Методом половинного деления (дихотомии) 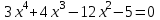 Зададим интервал  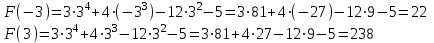  разобьем данный интервал разобьем данный интервал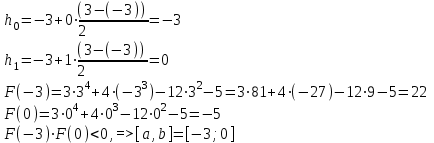 N=1 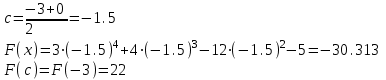 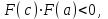 значения функция на концах имеют противоположные знаки, поэтому корень лежит в этом пределе, а именно значения функция на концах имеют противоположные знаки, поэтому корень лежит в этом пределе, а именно 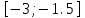 N=2 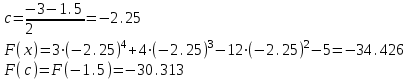 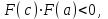 значения функция на концах имеют противоположные знаки, поэтому корень лежит в этом пределе, а именно значения функция на концах имеют противоположные знаки, поэтому корень лежит в этом пределе, а именно 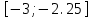 N=3 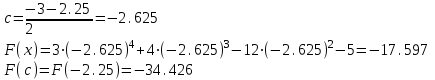 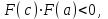 значения функция на концах имеют противоположные знаки, поэтому корень лежит в этом пределе, а именно значения функция на концах имеют противоположные знаки, поэтому корень лежит в этом пределе, а именно 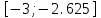 N=4 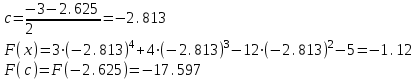 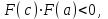 значения функция на концах имеют противоположные знаки, поэтому корень лежит в этом пределе, а именно значения функция на концах имеют противоположные знаки, поэтому корень лежит в этом пределе, а именно 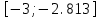 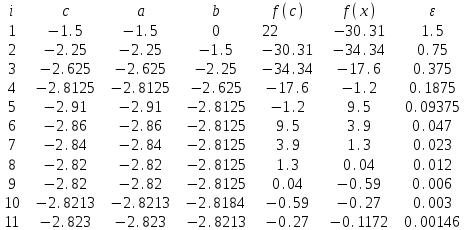 Нужный корень: 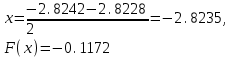 Ручной счёт Методом хорд 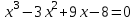 Первая производная: 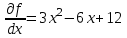 Вторая производная: 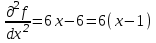 Зададим интервал  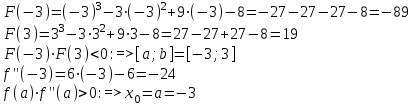  Ручной счёт Простой итерации для одного уравнения 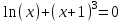 [2.1;2.2] – отрезок Первая производная: 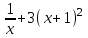 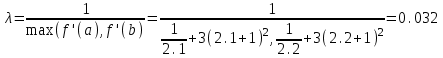 Возьмем произвольное приближение 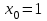 ; ;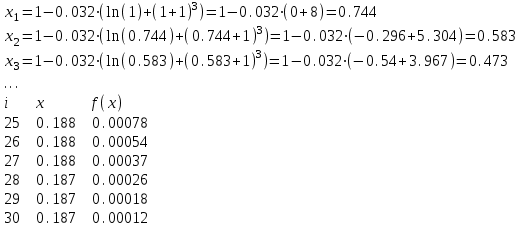 Ручной счёт Комбинированного метода 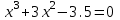 Первая производная: 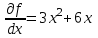 Вторая производная: 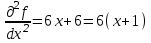 Зададим интервал  и разобьем на 4 подыинтервалов. и разобьем на 4 подыинтервалов. 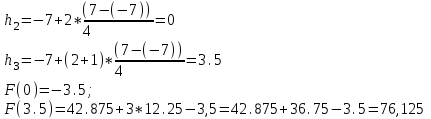 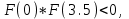 значения функция на концах имеют противоположные знаки, поэтому корень лежит в этом пределе, а именно значения функция на концах имеют противоположные знаки, поэтому корень лежит в этом пределе, а именно 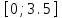 Требуется вычислить значения функции в точке 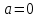 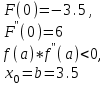 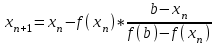 и и 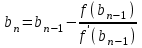 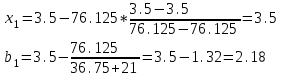  Искомый корень 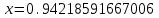 Проверка вычислений•Mathcad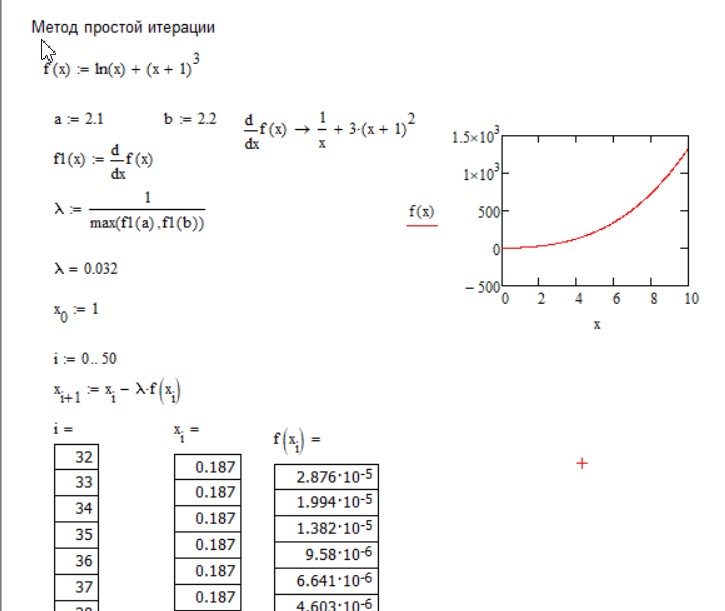 Рис. 1. Простая итерация (Одно уравнение)  Рис. 2. Простая итерация(Система) 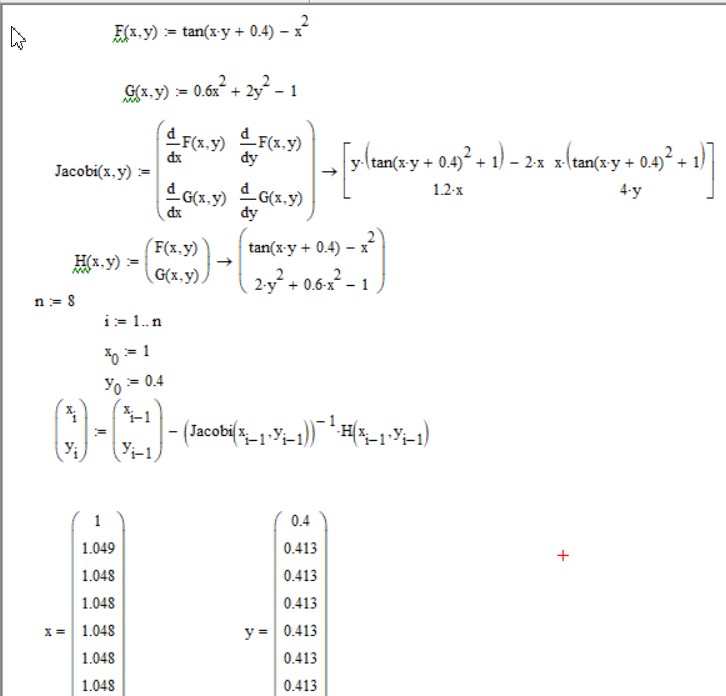 Рис. 3. Метод Ньютона 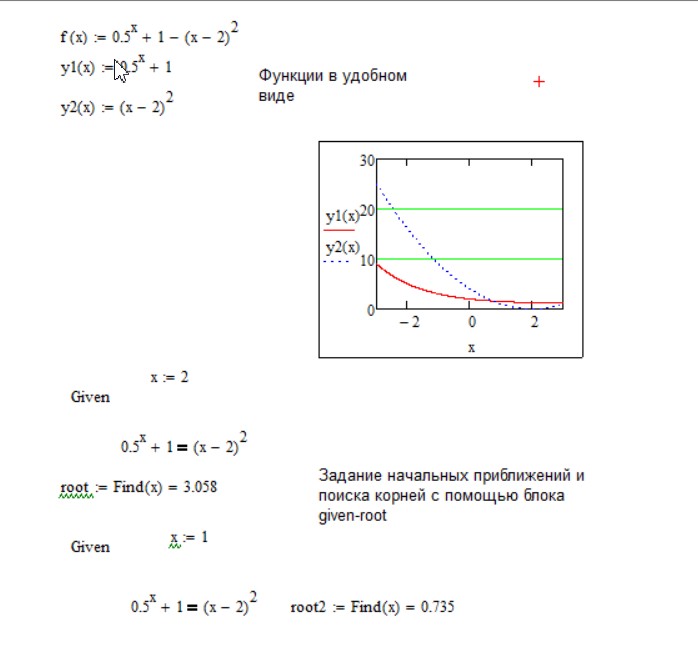 Рис. 4. Графический метод   Рис. 5. Метод половинного деления  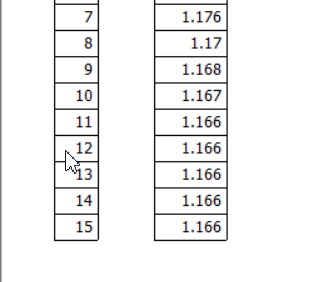 Рис. 6. Метод хорд   Рис. 7. Комбинированный метод •Excel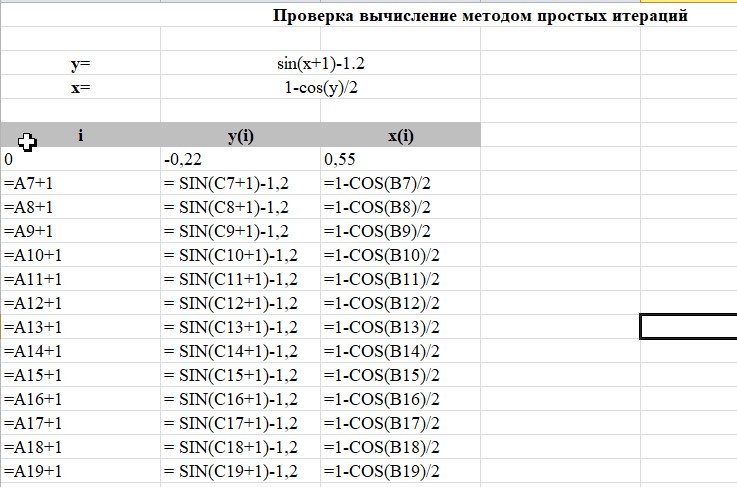 Рис. 9. Простая итерация (Формулы) 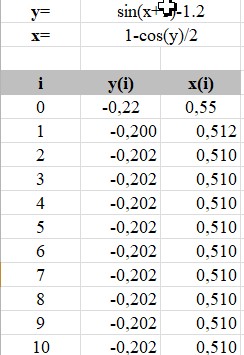 Рис. 8. Простая итерация (Результат) 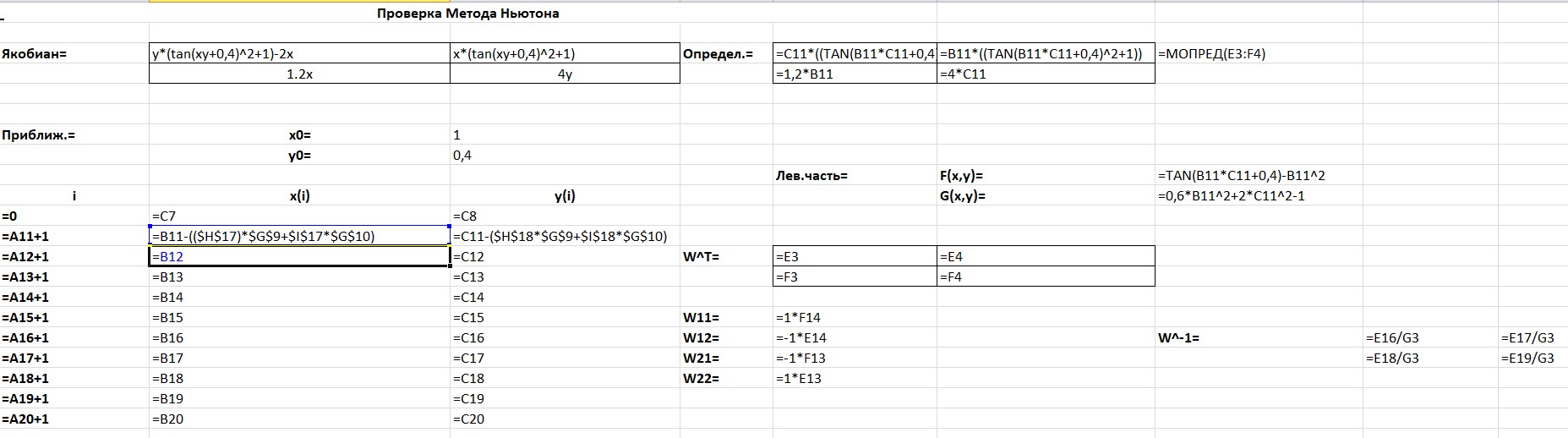 Рис. 9. Метод Ньютона (Формулы) 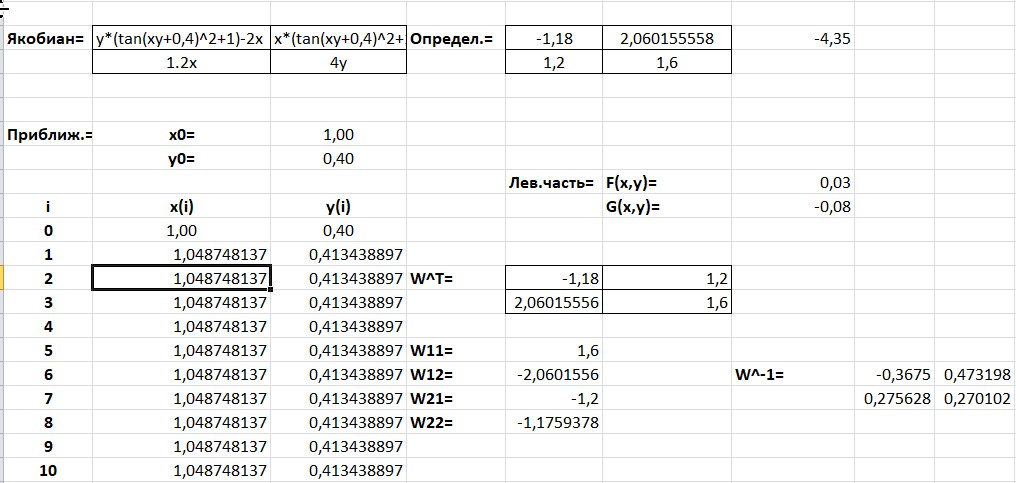 Рис. 10. Метод Ньютона (Результат) 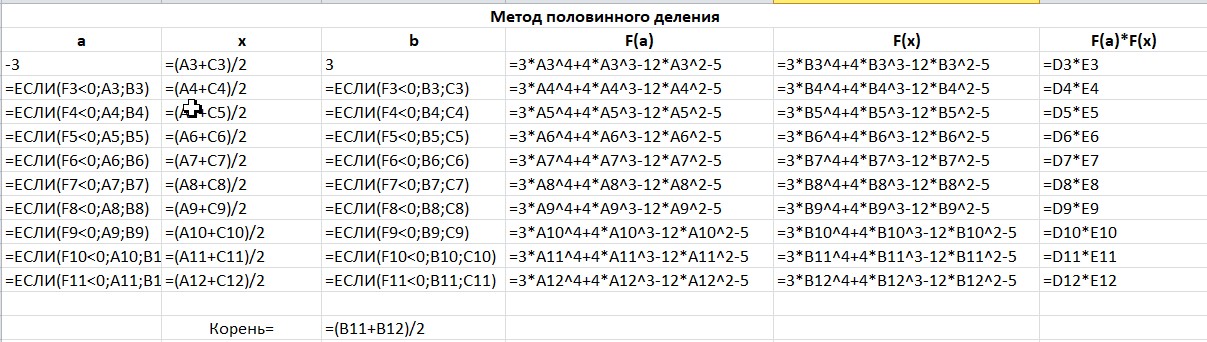 Рис. 13. Метод дихотомии (Формулы) 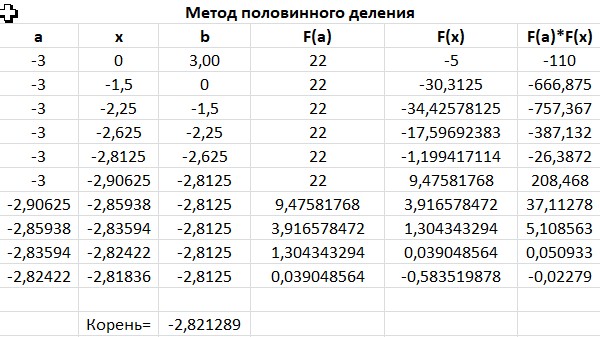 Рис. 11. Метод дихотомии (Результат) 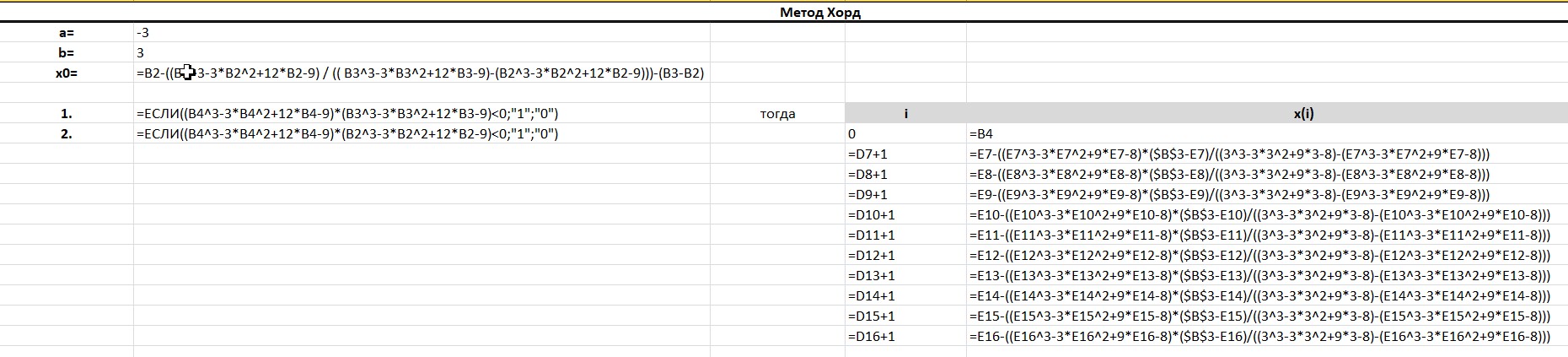 Рис. 12. Метод хорд (Формулы) 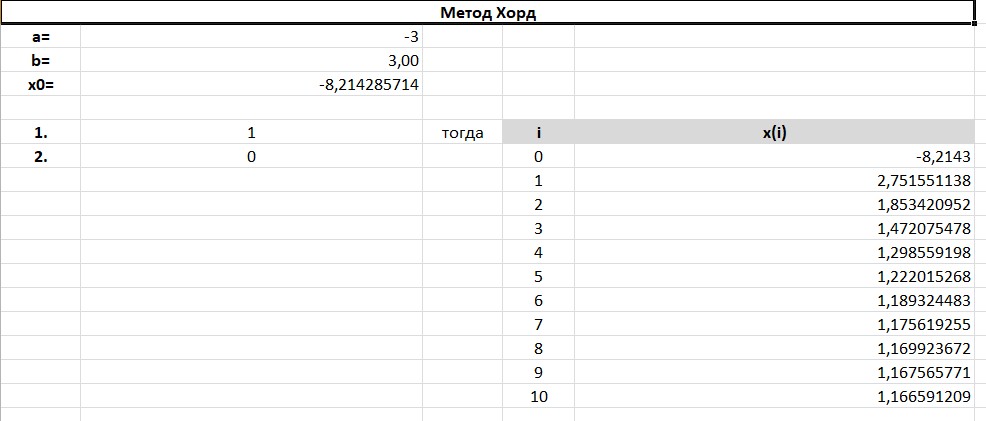 Рис. 13. Метод хорд (Результаты) 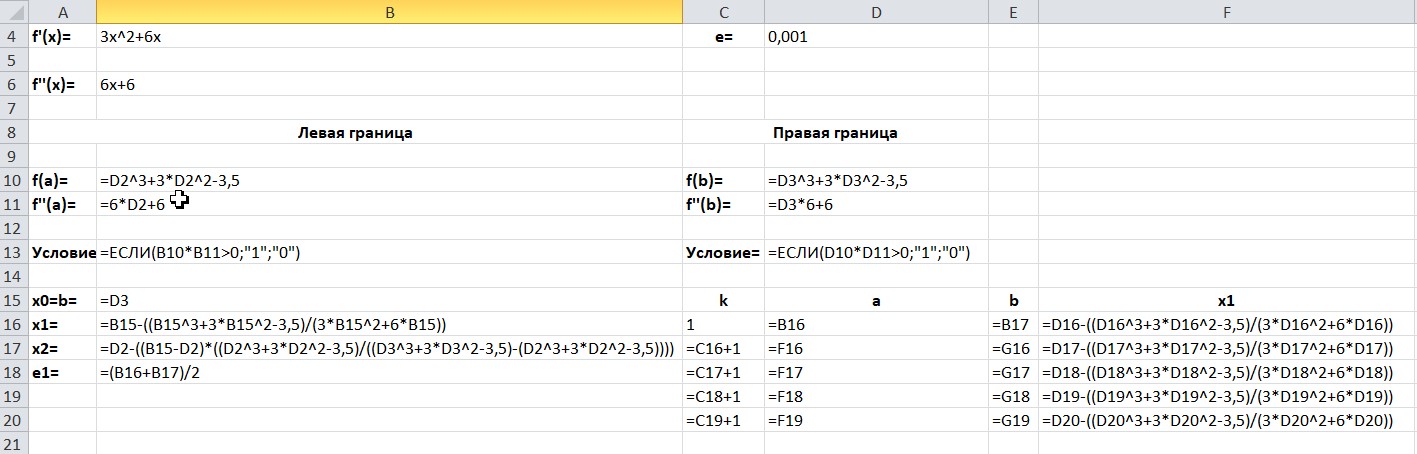 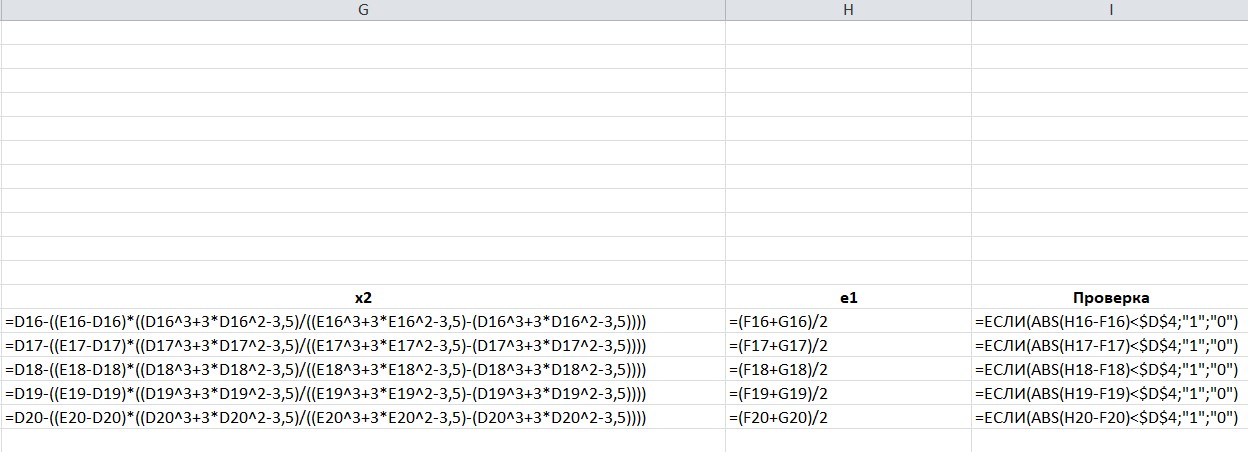 Рис. 14. Комбинированный метод (Формулы) 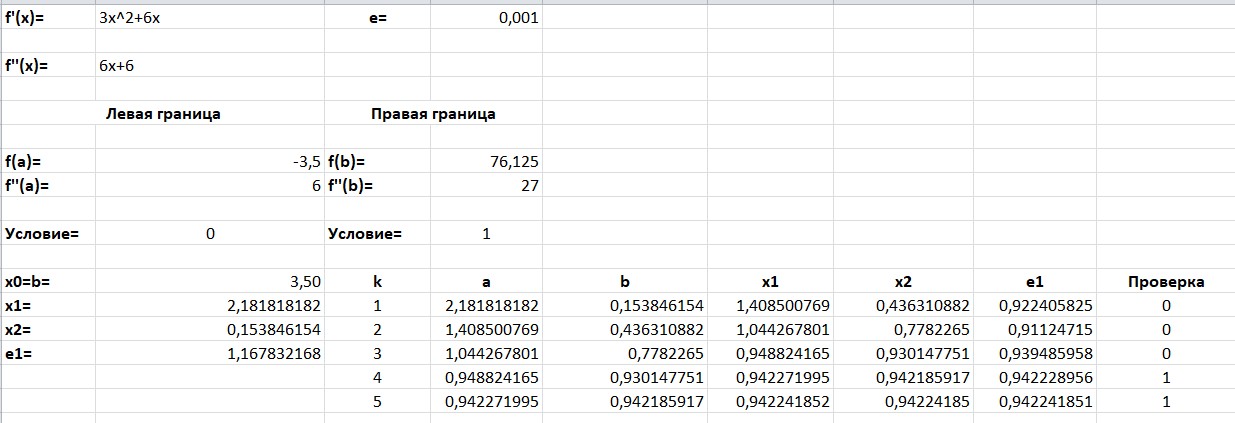 Рис. 15. Комбинированный метод (Результат) 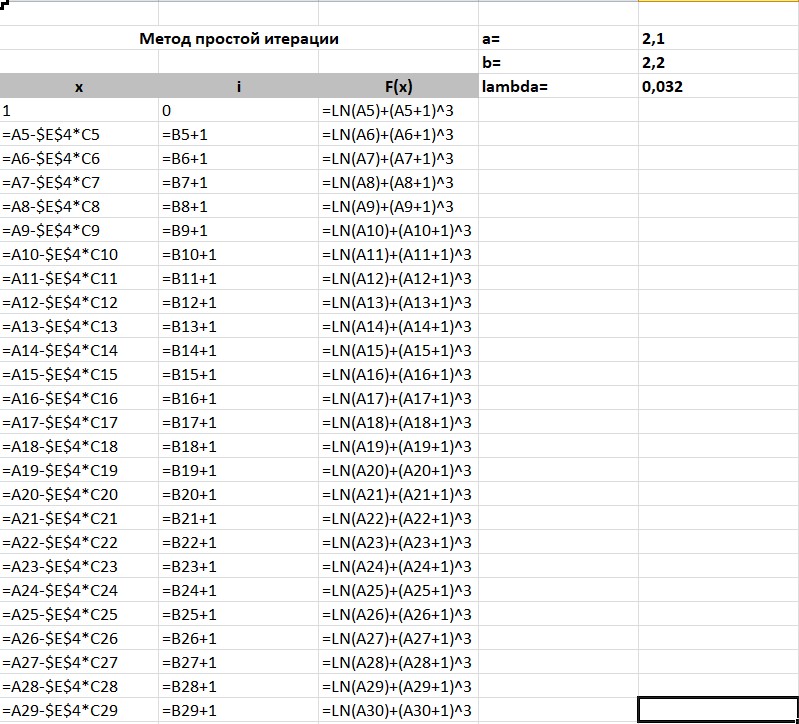 Рис. 16. Простая итерация (Одно уравнение) (Формулы) 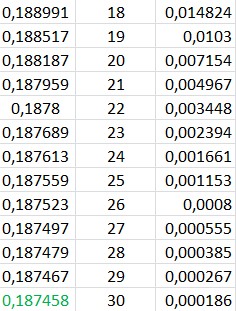 Рис.17. Простая итерация (Одно уравнение) (Результат) •C++#include using namespace std; int main() { setlocale(LC_ALL, "ru"); int k; // Кол-во итераций cout << "Введите кол-во итераций: "; cin >> k; double* x = new double[k]; double* y = new double[k]; cout << "Система уравнений:" << endl; /* y = sin(x+1)-1.2; x = 1-cos(y)/2; */ cout << "y = sin(x+1)-1.2" << endl; cout << "x = 1-cos(y)/2" << endl; cout << "\n"; cout << "Зададим начальное приближение: "; cout << "x0 = "; cin >> x[0]; cout << "y0 = "; cin >> y[0]; for (int i = 0; i < k; i++) { y[i+1] = sin(x[i] + 1) - 1.2; x[i+1] = 1 - (cos(y[0]) / 2); } cout << "Получим значения итераций:" << endl; for (int i = 0; i < k; i++) { cout << "x[" << i << "]: " << x[i] << " | "; cout << " y[" << i << "]: " << y[i] << endl; } } 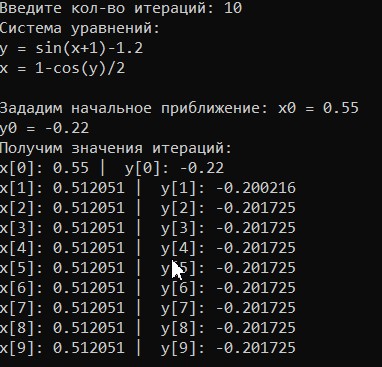 Рис. 18. Простая итерация #include using namespace std; int main() { setlocale(LC_ALL, "ru"); double* leftside = new double[2]; double Def; double** Jacobi = new double* [2]; for (int i = 0; i < 2; i++) { Jacobi[i] = new double[2]; } double** wT = new double* [2]; for (int i = 0; i < 2; i++) { wT[i] = new double[2]; } double W11, W12, W21, W22; double** invW = new double* [2]; for (int i = 0; i < 2; i++) { invW[i] = new double[2]; } int k = 10; // Кол-во итераций double* x = new double[k]; double* y = new double[k]; cout << "Дана система: " << endl; cout << "F(x,y) = tan(xy+0.4)-x^2\nG(x,y) = 0.6x^2+2y^2-1" << endl; cout << "Приближения функции: " << endl; x[0] = 1; y[0] = 0.4; cout << "x[0]: " << x[0] << endl; cout << "y[0]: " << y[0] << endl; for (int i = 0; i < k; i++) { Jacobi[0][0] = y[i] * (pow(tan(x[i] * y[i] + 0.4), 2) + 1) - 2 * x[i]; Jacobi[0][1] = x[i] * (pow(tan(x[i] * y[i] + 0.4), 2) + 1); Jacobi[1][0] = 1.2 * x[i]; Jacobi[1][1] = 4 * y[i]; Def = (Jacobi[0][0] * Jacobi[1][1]) - (Jacobi[0][1] * Jacobi[1][0]); wT[0][0] = Jacobi[0][0]; wT[0][1] = Jacobi[1][0]; wT[1][0] = Jacobi[0][1]; wT[1][1] = Jacobi[1][1]; W11 = 1 * wT[1][1]; W12 = -1 * wT[1][0]; W21 = -1 * wT[0][1]; W22 = 1 * wT[0][0]; invW[0][0] = W11 / Def; invW[0][1] = W12 / Def; invW[1][0] = W21 / Def; invW[1][1] = W22 / Def; leftside[0] = tan(x[i] * y[i] + 0.4) - pow(x[i], 2); leftside[1] = 0.6 * pow(x[i], 2) + 2 * pow(y[i], 2) - 1; x[i + 1] = x[i] - (invW[0][0] * leftside[0] + invW[0][1] * leftside[1]); y[i + 1] = y[i] - (invW[1][0] * leftside[0] + invW[1][1] * leftside[1]); cout << "x[" << i << "]: " << x[i] << " | y[" << i << "]: " << y[i] << endl; } delete[] leftside; delete[] Jacobi[2]; delete[] wT[2]; delete[] invW[2]; delete[] x; delete[] y; } 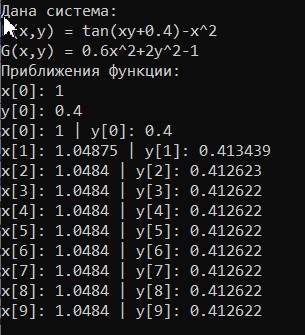 Рис. 19. МетодНьютона #include using namespace std; double function(double x) { return 3 * pow(x, 4) + 4 * pow(x, 3) - 12 * pow(x, 2) - 5; } double rootFinding(double (*f)(double), double a, double b, double e) { double c; while ((b - a) / 2 > e) { c = (a + b) / 2; if ((function(a) * function(c)) > 0) { a = c; } else { b = c; } } return c; } int main() { setlocale(LC_ALL, "ru"); double a, b, e, root; e = 0.01; cout << "Введите границы отрезка\n"; cout << "A: "; cin >> a; cout << "B: "; cin >> b; root = rootFinding(function, a, b, e); cout << "Корень уравнения = " << root << endl; cout << "F(x) = " << function(root) << endl; return 0; } 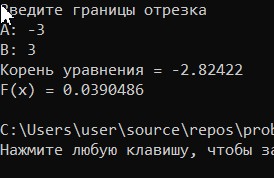 Рис. 20. Методдихотомии #include using namespace std; double function(double x); double MethodHord(double a, double b, double e); int main() { setlocale(LC_ALL, "ru"); double a, b, e; e = 0.001; cout << "Метод Хорд\n"; cout << "Введите границы интервала\n"; cout << "A: "; cin >> a; cout << "B: "; cin >> b; cout << "Результат: " << MethodHord(a, b, e) << endl; } double function(double x) { return pow(x, 3) - 3 * pow(x, 2) + 9 * x - 8; } double MethodHord(double a, double b, double e) { double c; double f_in_a = function(a); double f_in_b = function(b); while (abs(b - a) > e) { c = b - (a - b) / (f_in_a - f_in_b) * f_in_b; if (function(a) * function(c) < 0) { b = c; } else if (function(c) * function(b) < 0) { a = c; } else { return c; } } return c; } 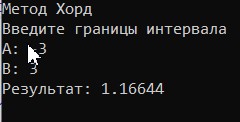 Рис. 21. Методхорд #include using namespace std; double f(double x) { return pow(x, 3) + 3 * pow(x, 2) - 3.5; } double f1(double x) { return 3 * pow(x, 2) + 6 * x; } double f2(double x) { return 6 *x + 6; } int main() { setlocale(LC_ALL, "ru"); double a, b, e, e1, x0, x1, x2; int i, n, k; cout << " Введите левую границу: "; cin >> a; cout << " Введите правую границу: "; cin >> b; e = 0.001; k = 0; if (f(a) * f2(a) > 0) { x0 = a; } else { x0 = b; } x1 = x0 - f(x0) / f1(x0); x2 = a - ((b - a) * f(a) / (f(b) - f(a))); e1 = (x1 + x2) / 2; while (abs(e1 - x1) > e) { a = x1; b = x2; x1 = a - f(a) / f1(a); x2 = a - ((b - a) * f(a) / (f(b) - f(a))); e1 = (x1 + x2) / 2; k++; cout << "k: " << k << " | x: " << x1 << endl; } cout << "LastIteration: " << k << " | Root: " << x1; } 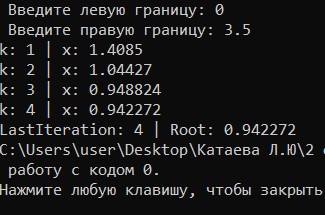 Рис. 22. Комбинированный метод #include #include using namespace std; double function(double x) { return log(x) + pow((x + 1), 3); } int main() { setlocale(LC_ALL, "ru"); int i; double x, a, b, lambda; lambda = 0.032; x = 1; cout << "Введите кол-во итераций: " << endl; cin >> i; for (int j = 0; j <= i; j++) { x = x - lambda * function(x); cout << "X[" << j << "]: " << x << endl; } cout << "Результат: " << i << "th iteration and x is " << x; } 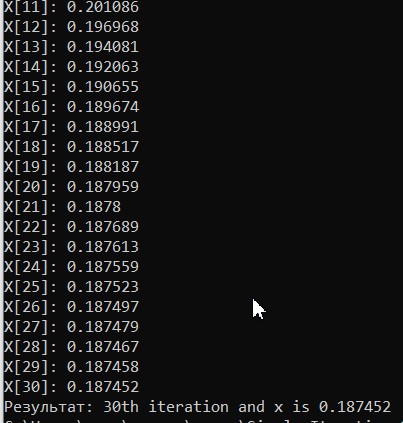 Рис. 23. Простая итерация для одного уравнения Заключение, выводы, погрешность, оценкаВ заключение можно сказать, что формулировка задачи была точно поставлена, а работа выполнена различными видами алгоритмов. Как показали результаты выше представленных алгоритмов, они все находятся в минимальных отклонениях друг от друга. Каждый алгоритм по-своему полезен и уникален, что даёт возможность рассмотрения результатов во всех плоскостях. Точность результатов зависела напрямую от используемого алгоритма, например: в шаговом методе использовался калькулятор, имеющий свои конфигурации для вычисления десятичных чисел, который, в свою очередь, может явно не совпадать с калькулирующим процессом того же языка программирования. С++. В конце концов, задача успешно выполнена и, если выбирать наиболее подходящий алгоритм для выполнения данной задачи, то им, определенно, будет Mathcad, в силу своей краткости, понятности и актуальности. ЛитератураГ.Н. Воробьева, А.Н. Данилова “Практикум по вычислительной математике”. изд.2., г. Москва, 1990г. Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков “Численные методы”, уч., МГУ им. М.В. Ломоносова, г.Москва, 2021г. Л.Ю. Катаева “Численные методы решения алгебраических и трансцендентных уравнений”. Н.Новгород, 2005г. |
