ЛР1 Численные методы. ЛР1. Методы решения нелинейных уравнений

• Название: Методы решения нелинейных уравнений
• Анкор: ЛР1 Численные методы
• Дата: 01.05.2022
• Размер: 93.35 Kb.
• Имя файла: ЛР1.docx
• Тип: Лабораторная работа; #506436

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Ордена Трудового Красного Знамени
федеральное государственное бюджетное образовательное
учреждение высшего образования

_______________________________________________

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СВЯЗИ И ИНФОРМАТИКИ

Кафедра информатики

Лабораторная работа №1

«Методы решения нелинейных уравнений»

Выполнил: студент группы БИН2009

Будашкин Евгений Павлович

Проверил:

Москва, 2021

1. Задание для решения нелинейных уравнений :



2. Отделение корней.

а) Графически

Код для получения графика :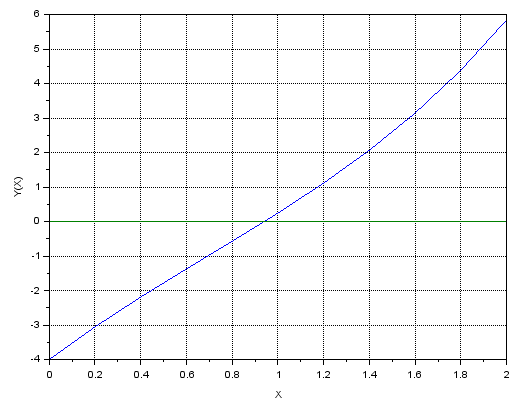





б) Аналитически :

Код для получения таблицы :



Выводимая таблица :



Вывод: На концах отрезка [0;1]функция имеет противоположные знаки, а 1-я производная знакопостоянна, следовательно, на этом отрезкеуравнение имеет единственный корень.

3. 
   Выполнение задания
   

3.1 Метод итерации

Код для получения таблицы :



Выводимая таблица :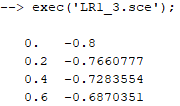


Вывод: условие сходимости метода итераций выполняется, поскольку на всем отрезке [a;b], |φ(x)|<1. Выберем например, начальное значение, x₀=0 (в методе итераций x₀– произвольное значение, принадлежащее отрезку [a;b]), и с использованием итерационной функции φ(x)=ln(4e^-x-1) выполним три итерации.

Расчет трех итераций:

n	xn	f(xn)
0	0	-4
1	1,6094379	3,2
2	0,5877867	-1,4222222
3	1,1700713	0,9808429

Погрешность:

Q=0.8

0.2/0.8*0.5822846=0.14557115

3. 
   Метод хорд:
   

1. 
   Исследование задания для «ручного расчета»
   

Проверка выполнения условия сходимости. Для сходимости метода необходимо знакопостоянство f’’(x) на отрезке [0.5;1].

Выбор начального приближения. Вид рекуррентной формулы зависит от того, какая из точек a или b является неподвижной. Неподвижен тот конец отрезка [a;b], для которого знак функции f(x) совпадает со знаком ее второй производной. Тогда второй конец можно принять за начальное приближение к корню, то есть точку .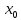

Знак функции совпадает со знаком второй производной в точке a=1. Следовательно, точка a является неподвижной точкой, а точка b является точкой начального приближения.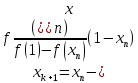



Расчет c точностью 10^-4:

//Сценарий для метода хорд
#include

#include

#include

using namespace std;
double fun(double x)

{

double f;

f = exp(x)-4*exp(-x)-1;

return(f);

}
double hord(double a, double b, double eps, double m1, double x0)

{

double t, x, c, pogr;

int n = 0;

x = x0;

if (x0 = a)

{

c = b;

}

else

{

c = a;

}

do

{

t = x;

n = n + 1;

x = x - (fun(x) * (c - x)) / (fun(c) - fun(x));

pogr = abs(fun(x)) / m1;

printf("%d %.5f %.5f %.5f\n", n, x, fun(x), pogr);

} while (pogr > eps);

printf("Koren= %.5f\n", x);

return 0;

}
int main()

{

double a = 1, b = 0.5, x0 = 0, eps = 0.0001, m1 = 4.1897996;

printf("n x f(b) pogr\n");

hord(a, b, eps, m1, x0);

system("PAUSE");

return 0;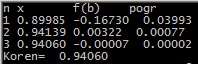

}



5. Решение нелинейного уравнения с использованием функции fsolve:

Код решения: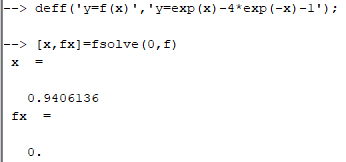


Вывод

В ходе выполнения лабораторной работы я смог выяснить, что метод Хорд показал меньшую погрешность, чем метод bnthfwbb. Также, с помощью метода хорд, мне удалось получить более точный корень (x = 0,9406137).