Лабораторная работа 2 Численные методы решения уравнений по дисциплине Математические методы построения алгоритмов
 Скачать 464.07 Kb.
|
|
Пензенский государственный университет Кафедра «Информационно-вычислительные системы» Лабораторная работа №2 «Численные методы решения уравнений» по дисциплине «Математические методы построения алгоритмов» Вариант № __ Выполнил: студент группы ______ ___________ Проверил: преподаватель СПО Звозникова И.П. Пенза, 2020 Цель работы Научится применять различные методы решения уравнений и оценивать точность полученных результатов. Задание Разработать программы для решения уравнения численными методами. Программа должна обеспечивать: - ввод границ интервала. - выбор метода решения. - ввод точности решения. - вывод корня уравнения и числа шагов поиска решения. - проверка существования корня на заданном интервале. -ввод начального приближения. Уравнение: ln(x) – x2 + 5 = 0 Для метода дихотомии точность принять равной 0.01; для остальных методов точность равной 0.001. Ход работы Построение графика функции f(x) = ln(x) – x2 + 5 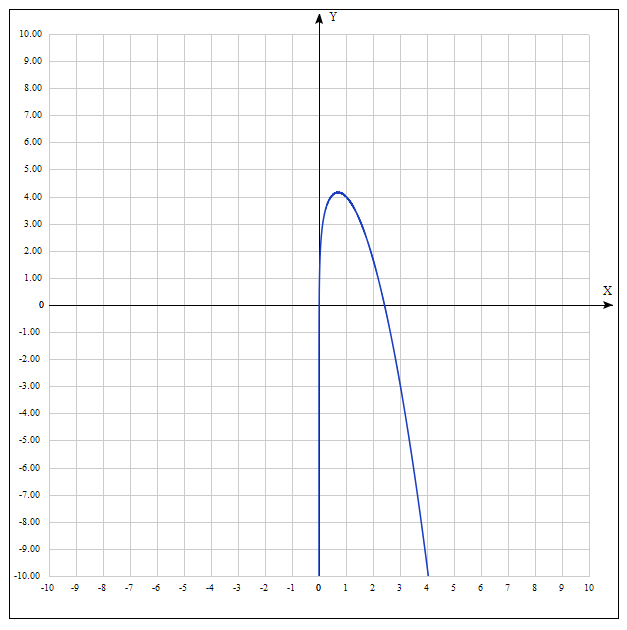 3.2 Локализация корней Из рисунка видно, что уравнение имеет 1 корень, который лежит в промежутке 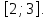 Функция должна быть непрерывной и монотонной на отрезке 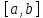 .  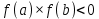Проверяем промежуток 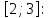 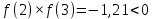  ледовательно, корень лежит на данном промежутке.Методы решения Данная задача может быть решена одним из 5 методов, для каждого из которых требуется выполнение ряда условий: 1) Метод половинного деления: Метод половинного деления (дихотомии) – непрерывность функции в промежутке [a,b]. Блок-схема метода приведена на рисунке 1. 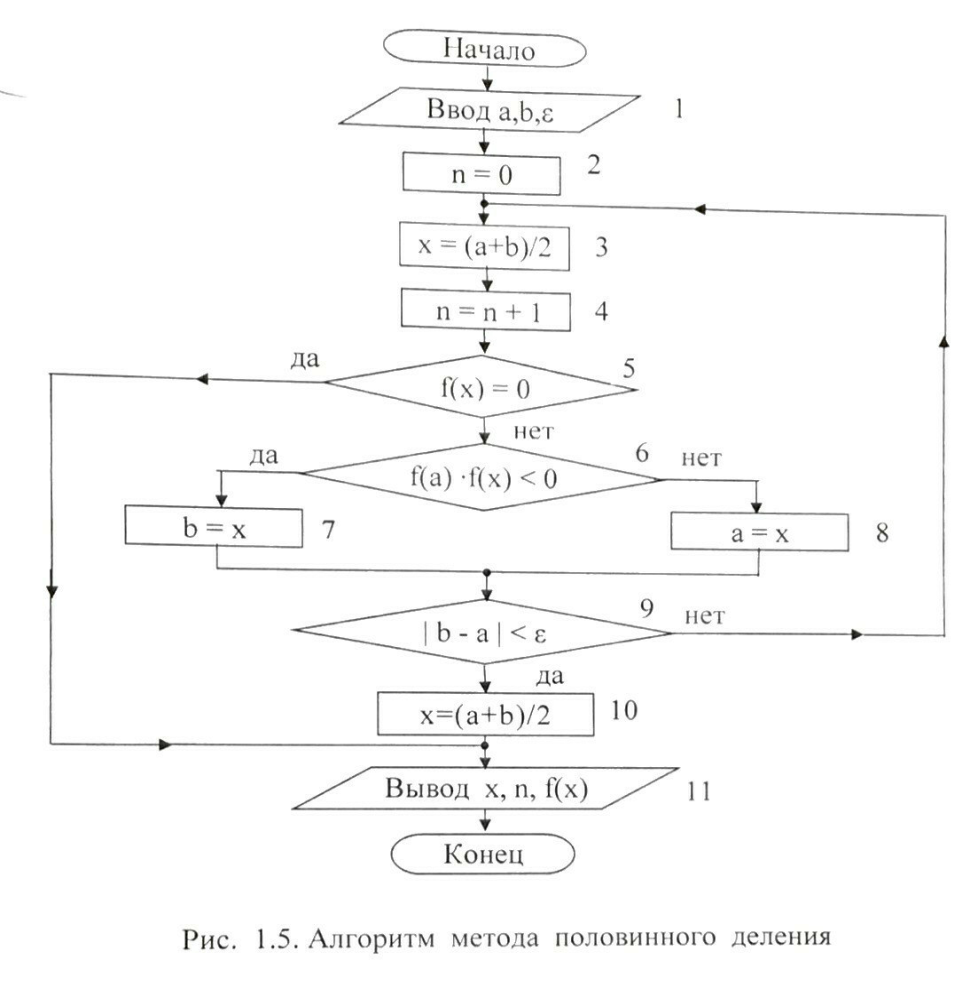 Рисунок 1 – Блок – схема для метода половинного деления 2) Метод итерации: Метод итерации – уравнение приведено к виду x = φ(x); на выбранном интервале [2; 3] выполняется неравенство | φ’(x)|<1. Представим уравнение в форме: φ(x) = x + 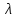 (ln(x) – x2 + 5)Найдем максимальное значение производной от функции f’(x)=ln(x) – x2 + 5 на отрезке [2; 3] 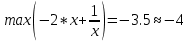 => λ =1/4=0.25Таким образом, получаем функцию: φ(x) = 0.25*ln(x) – 0.25*x2 +x +1.25 Блок-схема метода приведена на рисунке 2. 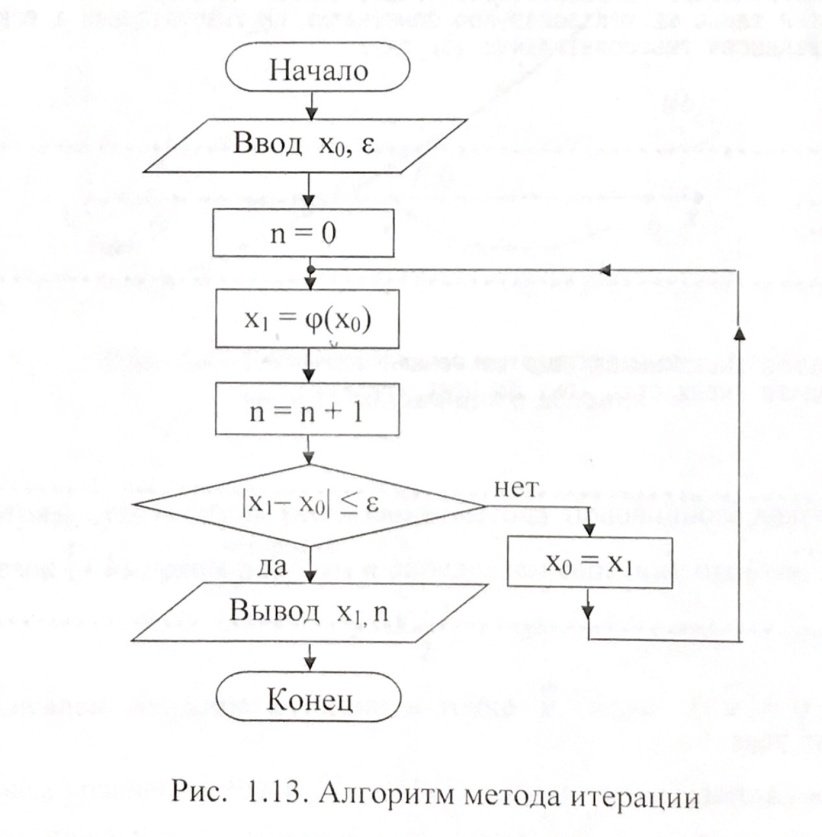 Рисунок 2 – Блок – схема для метода итераций 3) Метод Хорд: Метод Хорд – функция f(x) дважды дифференцируема, производные f’(x) и f’’(x) сохраняет знак на выбранном промежутке. Блок-схема метода приведена на рисунке 3. 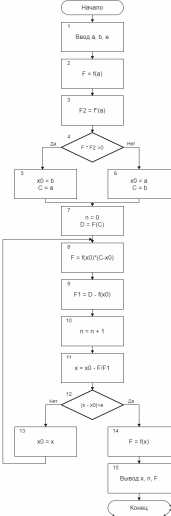 Рисунок 3 – Блок – схема для метода хорд 4) Метод Ньютона (касательных): Метод Ньютона – функция f(x) дважды дифференцируема, производные f’(x) и f’’(x) сохраняет знак на выбранном промежутке. Блок-схема метода приведена на рисунке 4. 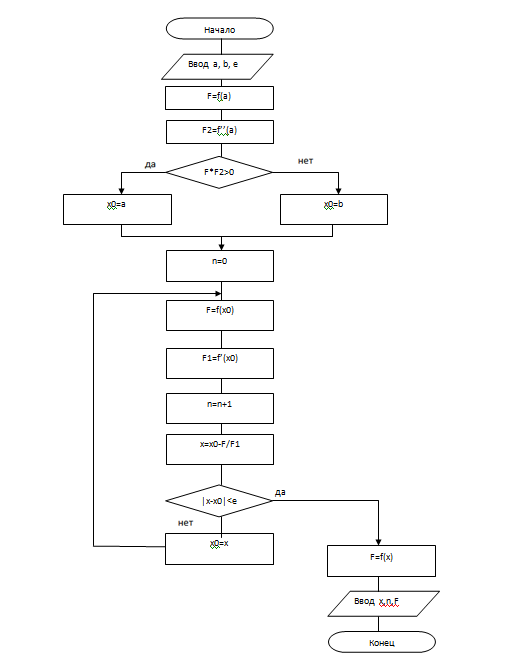 Рисунок 4 – Блок-схема для метода Ньютона Рисунок 4 – Блок – схема для метода касательных Рисунок 4 – Блок – схема для метода касательных 5) Комбинированный метод: Комбинированный метод – функция f(x) дважды дифференцируема, производные f’(x) и f’’(x) сохраняет знак на выбранном промежутке. Блок-схема метода приведена на рисунке 5. 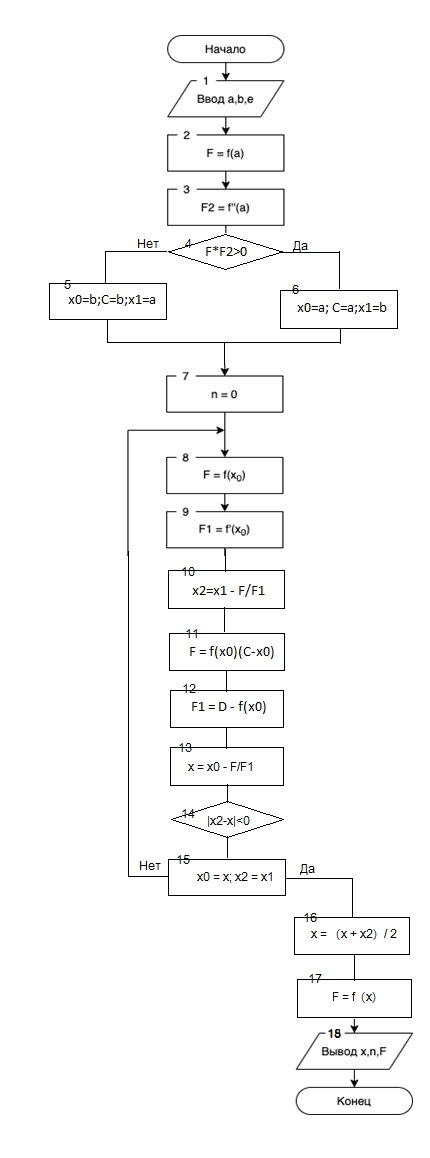 Рисунок 5 – Блок – схема для комбинированного метода 3.4 Таблица сравнения методов. Сравнение методов:
ТЕКСТ ПРОГРАММЫ Приложение А (обязательное) Вставить текст программы РЕЗУЛЬТАТЫ РАБОТЫ ПРОГРАММЫ Приложение Б (обязательное) Вставить результаты программы |