Аппаратура лаб 2. Лабораторная работа 2 Цифровые узлы в геофизической аппаратуре по дисциплине Аппаратура геофизических исследований составил
 Скачать 258.12 Kb.
|
|
Министерство образования и науки Российской Федерации федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тюменский государственный нефтегазовый университет» Институт геологии и нефтегазодобычи Кафедра «Прикладной геофизики» Лабораторная работа №2 Цифровые узлы в геофизической аппаратуре по дисциплине «Аппаратура геофизических исследований» СОСТАВИЛ: Студент группы ГИС-19-1 ______________Буторин Д.Г (подпись) « __ » __________ 2022г. Проверил: ____________Писарев А.Д. (подпись) « __ » __________ 2022г. г. Тюмень, 2022 г. Цель: познакомится с цифровыми узлами, использующихся в геофизической аппаратуре. Составить и расписать решение задачи с использованием цифровых узлов. Теоретическая часть Цифровыми называются устройства, в которых обрабатываемая информация имеет вид электрических сигналов с ограниченным множеством дискретных значений. В настоящее время в цифровых системах наибольшее распространение получили цифровые устройства, работающие с двоичным кодированием информации. Электрические сигналы в таких системах обычно имеют вид прямоугольных импульсов, характеризуемых двумя значениями уровней, высоким и низким. Элементы, используемые для обработки цифровых сигналов, называют логическими элементами. Современные логические элементы и цифровые устройства выполняются на основе интегральных микросхем. Цифровые устройства имеют принципиальные схемотехнические отличия от аналоговых устройств, обусловленные следующими факторами: менее жесткими требованиями к точности, стабильности параметров и характеристик элементов; возможностью синтеза систем любой сложности с помощью ограниченного набора базовых логических элементов и элементов памяти; возможностью сопряжения функциональных узлов без специальных согласующих элементов (благодаря использованию гальванической связи между функциональными узлами); простотой расширения функциональных возможностей путем набора требуемых сочетаний интегральных микросхем. Различают два основных класса цифровых устройств; комбинационные и последовательностные автоматы. В комбинационных автоматах определенному сочетанию входных сигналов (набору) соответствует определенный выходной сигал. Они, как правило, не обладают памятью. В последовательностных автоматах такая однозначность отсутствует. В них выходной сигнал зависит от совокупности входных сигналов как в текущий, так и в предыдущие моменты времени. Эти автоматы обладают памятью. В комбинационных автоматах наиболее широкое применение находят такие цифровые устройства, как сумматоры, дешифраторы и преобразователе кодов. В последовательностных автоматах широко используются цифровые устройства с двумя устойчивыми состояниями — триггеры. На их основе строят регистры, счетчики, схемы памяти. В алгебре логике различные логические выражения могут иметь только два значения: «истинно» или «ложно». Для обозначения истинности или ложности пользуются символами 1 и 0. Все возможные логические функции n переменных можно образовать с помощью треx основных операций; логического отрицания (инверсии, операции НЕ), логического сложения (дизъюнкции, операции ИЛИ), логического умножения (конъюнкции, операции И). Основные цифровые устройства реализующие данные функции выглядят следующим образом: 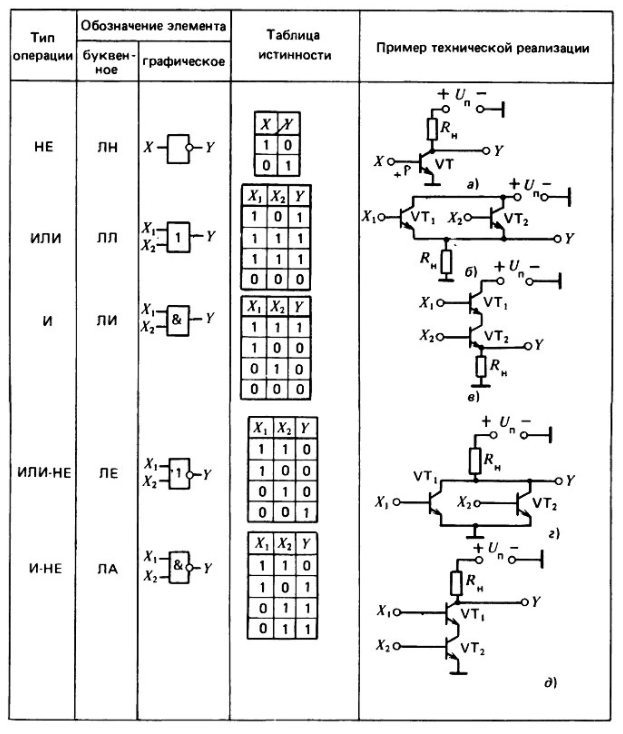 Также, существуют некоторые устройства, построенные на цифровой логике и применяющиеся там же. Такие как: машина Тьюрига, конечный и бесконечный автоматы и архитектура фон Неймана. Конечный автомат (КА) в теории алгоритмов — математическая абстракция, модель дискретного устройства, имеющего один вход, один выход и в каждый момент времени находящегося в одном состоянии из множества возможных. Является частным случаем абстрактного дискретного автомата, число возможных внутренних состояний которого конечно. При работе на вход КА поступают последовательно входные воздействия, а на выходе КА формирует выходные сигналы. Обычно под входными воздействиями принимают подачу на вход автомата символов одного алфавита, а на выход КА в процессе работы выдаёт символы в общем случае другого, возможно даже не пересекающегося со входным, алфавита. Помимо конечных автоматов существуют и бесконечные дискретные автоматы — автоматы с бесконечным числом внутренних состояний, например, машина Тьюринга. Машина Тьюринга представляет собой абстрактный исполнитель (абстрактная вычислительная машина). Она была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма. Машина Тьюринга является расширением конечного автомата и способна имитировать всех исполнителей (с помощью задания правил перехода), каким-либо образом реализующих процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен. То есть всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга. В состав машины Тьюринга входит неограниченная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.  Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные. Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма. Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной. Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: qiaj→qi1aj1dk (если головка находится в состоянии qi, а в обозреваемой ячейке записана буква aj, то головка переходит в состояние qi1, в ячейку вместо aj записывается aj1, головка делает движение dk, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации Архитектура фон Неймана (модель фон Неймана, Принстонская архитектура) - широко известный принцип совместного хранения команд и данных в памяти компьютера. Вычислительные машины такого рода часто обозначают термином «машина фон Неймана», однако соответствие этих понятий не всегда однозначно. В общем случае, когда говорят об архитектуре фон Неймана, подразумевают принцип хранения данных и инструкций в одной памяти. 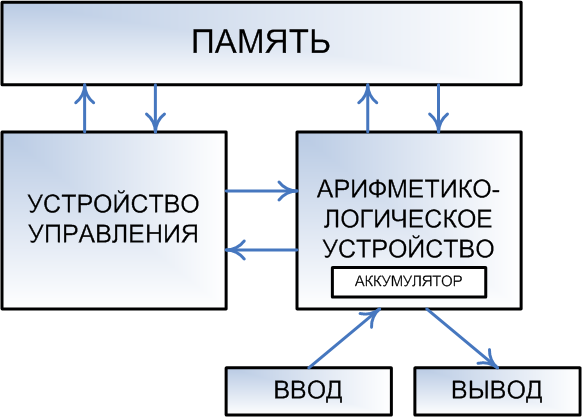 Узким местом архитектуры фон Неймона называют: С 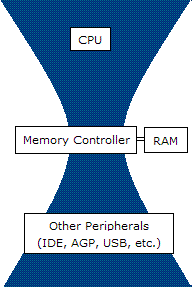 овместное использование шины для памяти программ и памяти данных приводит к узкому месту архитектуры фон Неймана, а именно ограничению пропускной способности между процессором и памятью по сравнению с объёмом памяти. Из-за того, что память программ и память данных не могут быть доступны в одно и то же время, пропускная способность канала «процессор-память» и скорость работы памяти существенно ограничивают скорость работы процессора — гораздо сильнее, чем если бы программы и данные хранились в разных местах.Данная проблема решается совершенствованием систем кэширования, что в свою очередь усложняет архитектуру систем и увеличивает риск возникновения побочных ошибок (например, проблема когерентности памяти). Практическая часть Задача: с помощью цифровых элементов изобразить устройство, которое из набора чисел от 0 до 15 покажет числа больше 7. Вывод: теоретической основой цифровых систем является алгебра логики, в которой принимаются только два значения: 0 и 1. Возможные логический операции можно образовать с помощью операций И, ИЛИ, НЕ. Также были изучены основные положения конечного и бесконечного автоматов, машины Тьюринга и архитектуры Фон Неймана, которые применяются с изменениями в современных компьютерах, в частности, в геофизической аппаратуре Было получено решение логической задачи о определении больше ли число, из промежутка от 0 до 15, 7-ми с помощью таблицы истинности, используемой для просмотра всевозможных вариантов. Получено восемь вариантов сочетаний аргументов для истинности данного высказывания. |