Практическая работа 4. Лабораторная работа 2 Исследование апериодического звена. Вариант 5 Выполнили студенты гр. Зээ204с брусницына Светлана Сергеевна
 Скачать 175.91 Kb. Скачать 175.91 Kb.
|
|
Министерство просвещения Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «Российский государственный профессионально- педагогический университет» Институт инженерно-педагогического образования Кафедра информационных систем и технологий Теория автоматического управления Лабораторная работа №2 Исследование апериодического звена. Вариант №5 Выполнили: студенты гр. ЗЭЭ-204С Брусницына Светлана Сергеевна Шифр зачетной книжки:18001385 Проверил: старший преподаватель Мешков Владислав Витальевич Екатеринбург РГППУ 2020 Цель работы: Изучение временных и частотных характеристик апериодического звена 1-го порядка; освоение способа экспериментального определения неизвестных параметров этого звена по его временным характеристикам. Порядок выполнения работы: В командном окне MATLAB нажав на иконку New выбираем меню Simulink Model. Открывается библиотека блоков Simulink Library Browser и пустое рабочее окно Simulink. В работе исследуется одно из апериодических звеньев 1-го порядка блок А5. Параметры этого блока скрыты от студента, они будут экспериментально определяться в ходе лабораторной работы. Перенесли звенья с заданным номером из библиотеки в рабочее окно Simulink. ИССЛЕДОВАНИЕ АПЕРИОДИЧЕСКОГО ЗВЕНА Задание 1. Определение коэффициента передачи и постоянной времени апериодического звена с заданным номером. 1) Снятие переходной функции апериодического звена. Схема для экспериментального определения переходной функции, собрана в окне Simulink. На вход исследуемого звена подается ступенчатый единичный сигнал от блока Step. На индикаторе наблюдаются входной и выходной сигналы звена, объединенные с помощью мультиплексора. 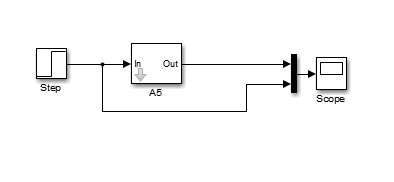 Рисунок 1 - Схема определения переходной функции Время окончания моделирования установлено: 1 секунду. 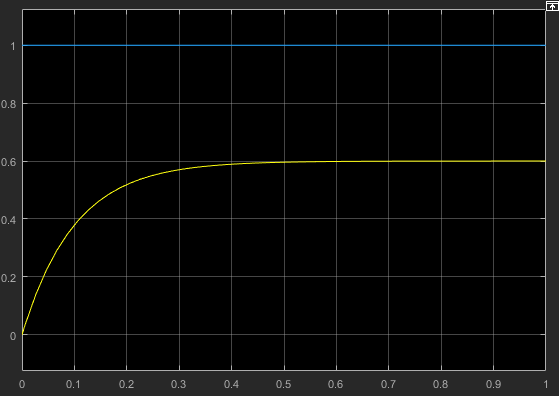 Рисунок 2 – График переходной функции, установившееся значение согласно графику равно 0,6 2) Снятие весовой функции апериодического звена. Схема для экспериментального определения весовой функции. Для определения весовой функции используется тот факт, что весовая функция является производной переходной функции. Для вычисления производной в библиотеку Simulink Library Browser включен блок Derivative (дифференцирующее звено). 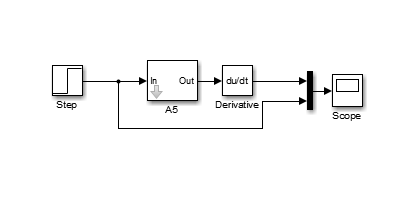 Рисунок 3 - Схема определения весовой функции 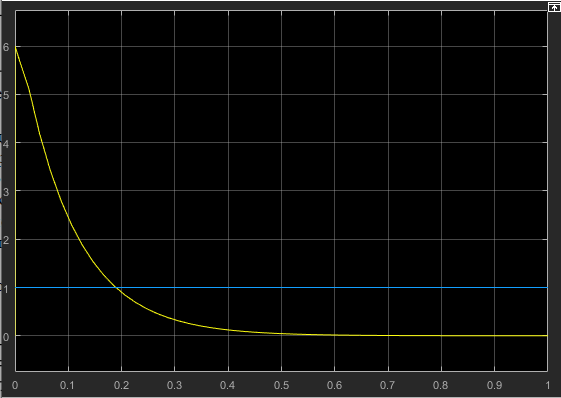 Рисунок 4 - Начальное значение весовой функции согласно графику = 6 3) Определение параметров апериодического звена. 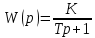 1. Установившееся значение переходной функции равно коэффициенту передачи звена К, т.е. K=0,6 2. Начальное значение весовой функции равно отношению коэффициента передачи звена к постоянной времени К/Т, т.е. 0,6/0,1= 6 3. Касательная к переходной функции в точке начала координат отсекает на линии установившегося значения отрезок равный постоянной времени Т, т.е. T=0,1 (согласно графику) 4. Линия t=T пересекает график переходной функции на уровне 0,378 от ее установившегося значения. 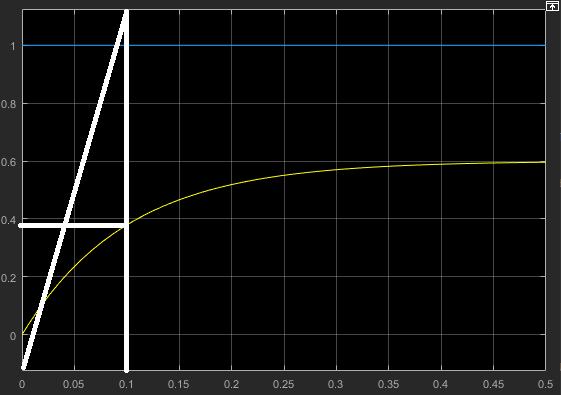 Рисунок 5 - Точка пересечения на графике переходной функции = 0,378 Согласно представленным данным, получим функцию: 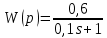 Проверка полученного результата: 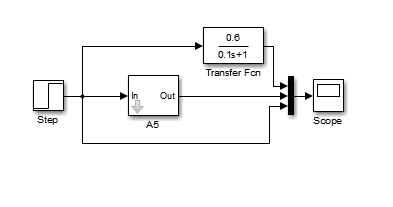 Рисунок 6 - Схема проверки полученного результата. Поместили в окно Simulink блок динамического звена «Transfer Fcn» и установили в нем передаточную функцию апериодического звена с найденными параметрами :w=tf(0,6,[0.1 1]) Подали на вход исследуемого звена с неизвестными параметрами и звена с найденными параметрами одновременно один и тот же ступенчатый сигнал. Графики совпали. 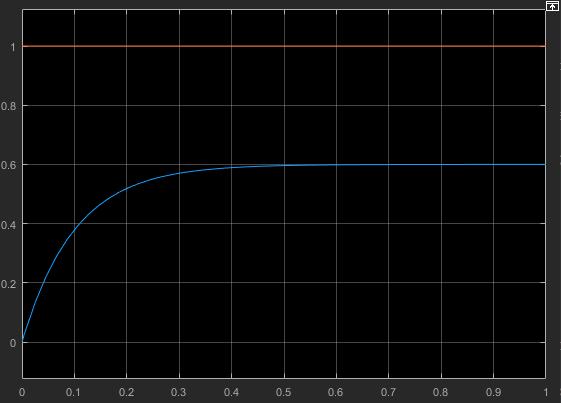 Рисунок 7 - График проверки ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК АПЕРИОДИЧЕСКОГО ЗВЕНА Задание 3. Получите частотные характеристики (АФЧХ и ЛЧХ) апериодического звена с найденными значениями параметров, используя функции Command Window, описанные в лабораторной работе №1. Сохраните частотные характеристики апериодического звена для отчета. Проверьте следующие утверждения на частотных характеристиках апериодического звена.  Рисунок 8 - Код построения АФЧХ 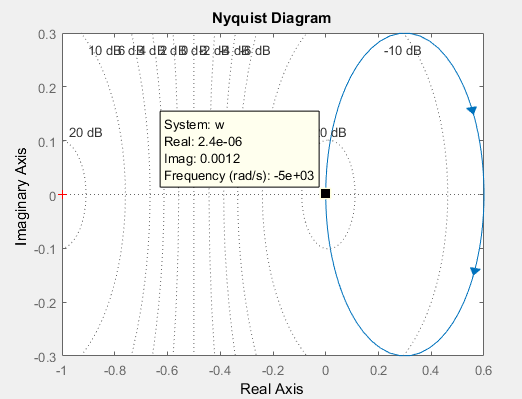 Начало АФЧХ (ὠ=0) находится на действительной оси в точке (К,0). 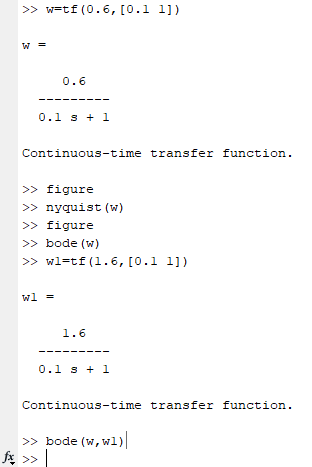 Рисунок 9 - Код построения ЛАЧХ 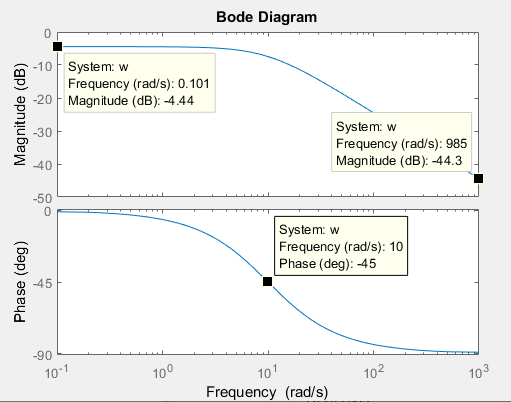 Значение ЛАЧХ в области низких частот (ὠ <<1/T) практически постоянно и равно -44,3. Наклон ЛАЧХ в области высоких частот (ὠ>>1/T) равен 10 дБ/дек. Значение ЛФЧХ на частоте ὠ=1/Т равно –45°.  Рисунок 10 - Код с измененным коэффициентом передач. 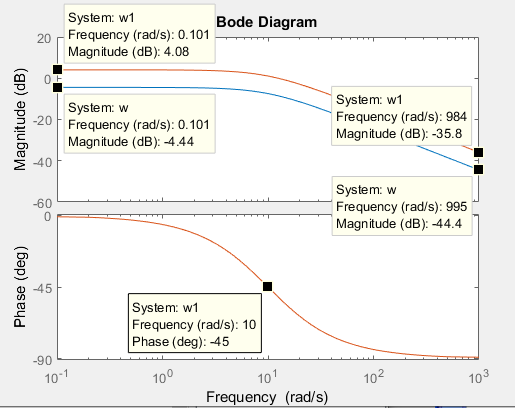 5) Изменение коэффициента передачи не влияет на ЛФЧХ. Для проверки последнего утверждения были построены в одном окне логарифмические частотные характеристики двух звеньев с одинаковыми постоянными времени и различными коэффициентами передачи Вывод: На основе проделанных опытов были изучены временные и частотные характеристики основных типов апериодического звена 1-го порядка, освоены способы экспериментального определения неизвестных параметров этих звеньев по их временным характеристикам. |
