ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ С ПОМОЩЬЮ МАЯТНИКА МАКСВЕЛЛА. Выполненная работа №2. Лабораторная работа 2 изучение закона сохранения энергии с помощью маятника максвелла
 Скачать 33.57 Kb. Скачать 33.57 Kb.
|
|
Лабораторная работа № 2 ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ С ПОМОЩЬЮ МАЯТНИКА МАКСВЕЛЛА Цель работы: Ознакомление со сложным движением твердого тела и изучение закона сохранения энергии на примере движения маятника Максвелла. Описание установки и метода изучения процесса Общий вид установки, используемой в настоящей работе, представлен на рис. 5.1. Маятник Максвелла представляет собой металлический диск 1, в середине которого укреплен металлический стержень 2. К концам этого стержня прикреплены две крепкие (капроновые) нити 3. Они наматываются на стержень (от концов его к диску). Диск маятника представляет собой непосредственно сам диск и сменные кольца, которые закрепляются на диске. При освобождении маятника он начинает движение: поступательное вниз и вращательное вокруг своей оси симметрии. 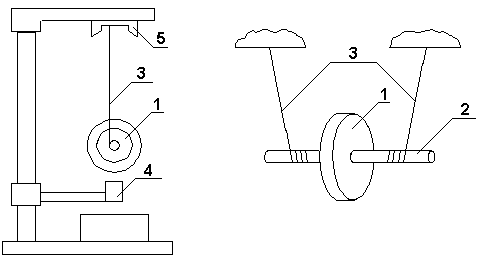 Вращение, продолжаясь по инерции в низшей точке движения (когда нити уже размотаны), приводит вновь к наматыванию нитей на стержень, а, следовательно, и к подъему маятника. Движение маятника после этого замедляется, маятник останавливается и снова начинает свое движение вниз и т.д. Ход маятника (расстояние, проходимое маятником) может быть измерено по вертикальной рейке с делениями, укрепленной на стойке. Уравнения движения маятника без учета сил трения имеют вид:  где m – масса маятника; I – момент инерции маятника; g – ускорение силы тяжести; r – радиус стержня; T – сила натяжения нити (одной); a – ускорение поступательного движения центра масс маятника; ε – угловое ускорение маятника. Ускорение a может быть получено по измеренному времени движения t и проходимому маятником расстоянию h из уравнения: a = 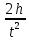 . .выражение для расчета теоретического значения ускорения движения центра тяжести маятника: a = 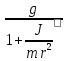 Скорость: V = at; угловая скорость: ω = εt. Полная кинетическая энергия маятника складывается из энергии поступательного перемещения центра масс (совпадающего с центром оси) и из энергии вращения маятника вокруг оси: 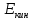 = = 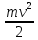 + + 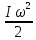 . .J = 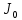 + + 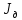 + +  ; ;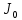 = = 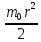 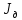 = = 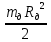  = = 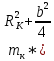 ) )Выполнение работы Результаты измерений и их обработка: Таблица 1. Результаты измерений и расчётов:
Экспериментальное значение ускорения 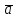 = = 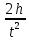 = = 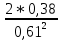 = 2,04 = 2,04 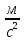 ; ;Средняя скорость:  = at = 2,04 * 0,61 = 1,25 = at = 2,04 * 0,61 = 1,25 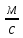 ; ;Угловая скорость: 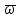 = =  *Rк = 1,25 * 0,048 = 0,06 *Rк = 1,25 * 0,048 = 0,06 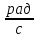 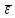 = = 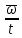 = = 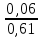 = 0,1 = 0,1 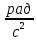 m = 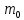 + + 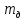 + + 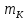 = 0,019 + 0,1+ 0,261 = 0,38 кг; = 0,019 + 0,1+ 0,261 = 0,38 кг;Момент инерции 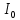 = = 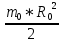 = = 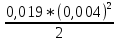 = 0,152 * = 0,152 * 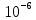 кг * кг * 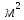 ; ;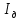 = = 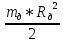 = = 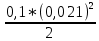 = 0,22 * = 0,22 * 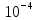 кг * кг * 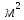 ; ;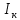 = =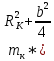 ) = 0,048 * ( ) = 0,048 * (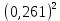 + + 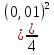 = 32,71 * = 32,71 * 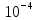 кг * кг * 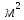 ; ;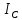 = = 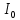 + + 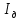 + + 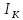 = (0,41 + 115 + 601) * = (0,41 + 115 + 601) * 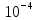 = 32,9315 * = 32,9315 * 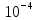 кг * кг * 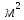 Теоретическое значение ускорения: a = 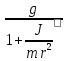 = = 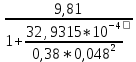 = 2,06 = 2,06 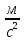 Кинетическая энергия: 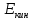 = = 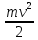 + + 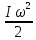 = = 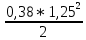 + + 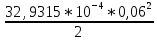 = 0,3 Дж = 0,3 Дж Расчёт относительной погрешности расхождения теоретического и экспериментального значений ускорения: 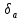 = = 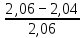 * 100 % = 1 %. * 100 % = 1 %.Вывод: В лабораторной работе измерено время движения маятника Максвелла, нагруженного дополнительным диском и кольцом. Рассчитаны экспериментальное и теоретическое значения ускорения маятника, они отличаются незначительно. Произведён расчёт линейной и угловой скорости, углового ускорения, момента инерции и кинетической энергии. Ответы на контрольные вопросы: Что называется моментом инерции? Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Что представляет собой маятник Максвелла? Маятник Максвелла представляет собой металлический диск 1, в середине которого укреплен металлический стержень 2. К концам этого стержня прикреплены две крепкие (капроновые) нити 3. Они наматываются на стержень (от концов его к диску). Диск маятника представляет собой непосредственно сам диск и сменные кольца, которые закрепляются на диске. При освобождении маятника он начинает движение: поступательное вниз и вращательное вокруг своей оси симметрии. Запишите уравнения движения маятника.  4. Выведите формулу ускорения движения центра масс маятника. Из уравнений движения: 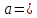 g - g - 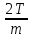 T = 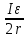 ε = 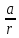 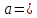 g - g - 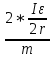 = g - = g - 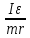 = g - = g - 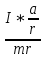 = g - = g - 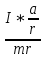 = g - = g - 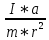 a = 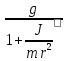 | ||||||||||||||||||||||||||||||||||||||||||||||

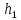 = 38 см = 0,38 м;
= 38 см = 0,38 м; 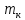 = 0,261 кг, R0= 0,004 м – радиус оси;
= 0,261 кг, R0= 0,004 м – радиус оси;