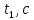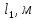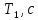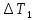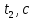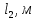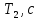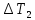Изучение законов колебательного движения. Потатуев Денис Сергеевич РЭА-31-21 лаб раб 2 механика. Лабораторная работа 2 Изучение законов колебательного движения студент группы рэа3121 Потатуев Денис Сергеевич Допуск
 Скачать 57.96 Kb. Скачать 57.96 Kb.
|
|
Федеральное государственное образовательное учреждение высшего профессионального образования «Чувашский государственный университет им. И. Н. Ульянова» Кафедра общей физики Лабораторная работа №2 Изучение законов колебательного движения Выполнил: студент группы РЭА-31-21 Потатуев Денис Сергеевич Допуск Выполнение Защита Чебоксары 2022 1. Цель работы - Изучение законов колебательного движения, измерение ускорения свободного падения с помощью математического маятника. 2. Приборы и принадлежности: математический маятник, миллисекундомер. 3. Теория Физическим маятником называется твердое тело, совершающее колебания относительно неподвижной горизонтальной оси, не проходящей через центр масс под действием силы тяжести (рис. 1). 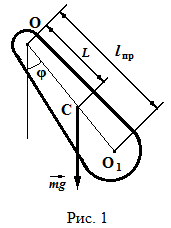 При отклонении маятника от положения равновесия на угол φ сила тяжести создает момент 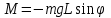 (1) (1)где m – масса маятника, L – расстояние от оси вращения до центра масс системы. Знак «минус» показывает, что момент силы тяжести стремится вернуть маятник в положение равновесия, т.е. уменьшить угол φ. Если обозначить момент инерции маятника относительно оси О через J, то уравнение движения маятника в отсутствии трения запишется в виде 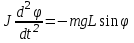 (2) (2)где 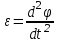 – угловое ускорение. При малых углах отклонения sinφ ≈ φ, тогда уравнение (2) примет вид – угловое ускорение. При малых углах отклонения sinφ ≈ φ, тогда уравнение (2) примет вид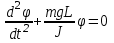 (3) (3)Непосредственной подстановкой можно убедиться, что частным решением дифференциального уравнения (3) является функция φ = φ0cosωt (4) Из выражения (4) следует, что при малых колебаниях в отсутствии трения физический маятник совершает гармонические колебания с циклической частотой 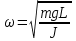 (5) (5) Следовательно, период колебания физического маятника 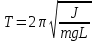 (6) (6)Как видно из формул (5) и (6), частота ω и период Т определяются параметрами физического маятника. Математическим маятником называется материальная точка, подвешенная к неподвижной опоре с помощью нерастяжимой и невесомой нити. Близким к математическому маятнику является тяжелый шарик, подвешенный на длинной тонкой нити. Момент инерции математического маятника относительно оси вращения, проходящей через точку подвеса: 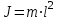 (7) (7)Следовательно, период колебания математического маятника с учетом выражений (6) и (7) 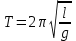 (8) (8)Из формулы (8) видно, что период колебания математического маятника не зависит от массы и амплитуды. Формула (8) справедлива лишь для малых углов отклонения от положения равновесия, т.е. при малых амплитудах. Если угол отклонения φ> 4о, то более точное выражение для периода имеет вид 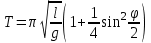 (9) (9)Экспериментально определив длину и период колебаний математического маятника, можно найти ускорение свободного падения (упр. 1). Из сопоставления формул (6) и (8) следует, что математический маятник с длиной 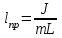 (10) (10)будет иметь такой же период, что и физический маятник. Величина lпр называется приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника. Точка О1 (рис. 1), лежащая на прямой, соединяющей точку подвеса О с центром масс С, и отстоящая от точки подвеса на расстоянии lпр, называется центром качания физического маятника. Точка подвеса и центр качания взаимообратимы. Если точку подвеса перенести в центр качания, то новый центр качания совпадет с положением прежней точки подвеса, т.е. приведенная длина и период колебаний маятника останутся прежними. Таким образом, если у физического маятника найдены две точки подвеса, лежащие по разные стороны от центра масс, и периоды колебаний при этом совпадают, то расстояние между ними равно приведенной длине физического маятника. На этом свойстве основан метод определения ускорения свободного падения с помощью оборотного маятника (упр. 2). Описание экспериментальной установки 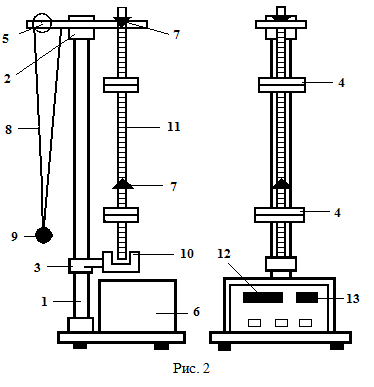 Экспериментальная установка представлена на рис. 2. На вертикальной стойке 1 установки размещены два кронштейна: верхний и нижний с фотоэлектрическим датчиком. Верхний кронштейн 2 может поворачиваться вокруг вертикальной оси и фиксироваться в любом выбранном положении. С одной стороны кронштейна подвешен математический маятник, с другой –физический (оборотный) маятник. Математический маятник представляет собой стальной шарик 9, подвешенный на бифилярном подвесе 8. Длину математического маятника можно регулировать при помощи воротка 5, а ее величину можно измерить по миллиметровой шкале, нанесенной на вертикальной стойке установки. Физический (оборотный) маятник представляет собой стальной стержень 11 с двумя грузами 4. Маятник может подвешиваться к верхнему кронштейну с помощью двух опорных призм 7. Грузы и опорные призмы могут перемещаться вдоль стержня и фиксироваться в определенных положениях. Для этого на стержне сделаны кольцевые выточки, нанесенные через 10 мм, позволяющие надежно фиксировать грузы и опорные призмы с точностью 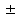 0,5 мм. На нижнем кронштейне 3 смонтирован фотоэлектрический датчик, подающий сигнал окончания времени счета и числа колебаний на цифровой миллисекундомер 6. Кронштейн с фотоэлектрическим датчиком может перемещаться по вертикальной стойке и фиксироваться в любом положении. Измерение времени и числа колебаний производится с помощью цифровых индикаторов 12 и 13. 0,5 мм. На нижнем кронштейне 3 смонтирован фотоэлектрический датчик, подающий сигнал окончания времени счета и числа колебаний на цифровой миллисекундомер 6. Кронштейн с фотоэлектрическим датчиком может перемещаться по вертикальной стойке и фиксироваться в любом положении. Измерение времени и числа колебаний производится с помощью цифровых индикаторов 12 и 13.Точность определения длины математического маятника по шкале прибора не менее 2 мм. Погрешность измерения времени не более 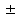 0,02%. 0,02%.Упражнение 1 Определение ускорения свободного падения с помощью математического маятника. Если известны периоды колебаний двух математических маятников с различными длинами 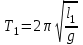 и и 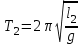 (11) (11)то ускорение свободного падения можно вычислить по формуле 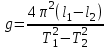 (12) (12)Таким образом, для определения ускорения свободного падения необходимо измерить периоды колебаний и разность длин двух математических маятников. 4. Результаты и расчеты.
Примем значение надежности 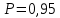 и коэффициент Стьюдента для пяти измерений и коэффициент Стьюдента для пяти измерений 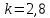 . Периодов . Периодов 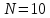 . .Вычисление периодов: 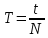 Вычисление случайных погрешностей: 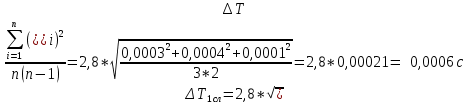 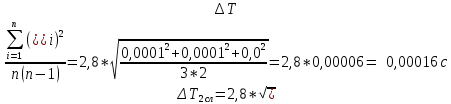 Вычисление среднего значения ускорения свободного падения: 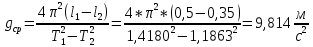 Вычисление относительной погрешности: 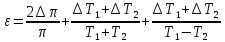 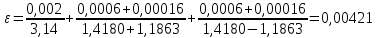 Вычисление абсолютной погрешности измерения объема кольца: 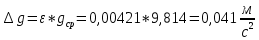 5. Окончательный результат: 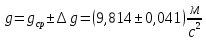 Контрольные вопросы и задания 1. Что называется приведённой длиной физического маятника? Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника. 2. Выведите формулу для периодов физического и математического маятников. 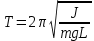 и и 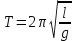 3. Что такое центр физического маятника качания? Каким свойством он обладает? Центр качания физического маятника — это такая точка О1 (рис. 1), лежащая на прямой, соединяющей точку подвеса О с центром масс С, и отстоящая от точки подвеса на расстоянии lпр. 4. Почему для определения ускорения свободного падения используется два математических маятников с разными длинами? Если известны периоды колебаний двух математических маятников с различными длинами, то ускорение свободного падения можно вычислить по формуле 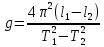 Таким образом, для определения ускорения свободного падения необходимо измерить периоды колебаний и разность длин двух математических маятников. 5. Почему амплитуда колебаний математического и физического маятников должны быть малой? Амплитуда должна быть небольшой, потому что период времени не зависит от амплитуды правило применяется к маятникам только в том случае, если они демонстрируют простое гармоническое движение. 6. Как устроен оборотный маятник? Оборотный маятник – это такой маятник, у которого имеются две расположенные вблизи его концов опорные призмы, за которые он поочередно может подвешиваться. Вдоль маятника могут закрепляться и перемещаться тяжелые грузы. Перемещением грузов добиваются того, чтобы при подвешивании за любую призму период колебаний был одинаков. 6. Вывод: приблизительное значение ускорения свободного падения с вероятностью 95% лежит в найденном интервале. Изучил законы колебательного движения. |