Лр№2 Медведева Кожевникова. Лабораторная работа 2 Компьютерная обработка результатов эксперимента

• Название: Лабораторная работа 2 Компьютерная обработка результатов эксперимента
• Дата: 19.12.2022
• Размер: 174.65 Kb.
• Имя файла: Лр№2 Медведева Кожевникова.docx
• Тип: Лабораторная работа; #853611

Лабораторная работа №2 «Компьютерная обработка результатов эксперимента»

1. 
   Цель работы: По результатам кинетического эксперимента, в котором варьировались концентрации исходных реагентов, и измерялась скорость химической реакции, идентифицировать параметры математической модели кинетики сложной химической реакции: константу скорости (k) и порядки реакции по компонентам (𝐴_𝑖). Общий вид модели: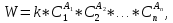
   

где W – скорость химической реакции, C_i –концентрация i-го компонента, n – число компонентов.

2. 
   Практическое задание: эксперимент выполняет программа
   

WRKWWW.EXE. Исходные данные представлены ниже:

• 
  шифр задания – opt18;
  
• 
  число опытов – m = 30; число веществ – n = 5; определений скорости – L = 3;
  
• 
  ожидаемые результаты:
  
  • 
    константа скорости – k = 17,05; дисперсия – S_к = 0,16;
    
  • 
    порядки р-ции: A₁ = 1,2; A₂ = 1,2; A₃ = 1,4; A₄ = 1,4; A₅ = 1;
    
• 
  возможны выбросы в точках 2 и 21.
  

Полный маршрут до файла с результатами эксперимента: E:\kurs2\gr2-21\opt18.dat

3. Постановка задачи регрессионного анализа

Для удобства идентификации параметров нелинейной математической модели кинетики химической реакции путем логарифмирования представим её в виде линейной многофакторной регрессии:

Y = b₀ + b₁X₁ + b₂X₂ + 𝑏₃X₃ + b₄X₄,

где Y – среднее от логарифмов измерений скоростей, 𝑋_𝑖 = ln (𝐶_𝑖), 𝑏_𝑖 – коэффициенты регрессии, причем 𝑏₀ = ln (𝑘), 𝑏_𝑖 = 𝐴_𝑖, 𝑖 = 1 … 𝑛 – факторы, n

= 5 – число факторов (веществ).

Для обратного перехода от регрессии к уравнению кинетики будет необходимо рассчитать константу скорости: 𝑘 = 𝑒^𝑏0 , а порядки реакции по компонентам будут соответствовать коэффициентам регрессии (𝐴_𝑖 = 𝑏_𝑖,).

4. Выполнение работы:

1. 
   Подготовка таблицы результатов в пакете STATISTICA:
   
   • 
     выполнен импорт файла данных в таблицу; переменные в исходной таблице переименованы (𝐶1 … 𝐶5, 𝑊1 … 𝑊3);
     
   • 
     добавлены и рассчитаны по формулам 16 новых переменных:
     
     • 
       X1…X5 – логарифмы концентраций (𝑋_𝑖 = ln (𝐶_𝑖));
       
     • 
       Y1…Y3 – логарифмы скоростей (𝑌_𝑖 = ln (𝑊_𝑖));
       
     • 
       Y – среднее от Y1 – Y3 ( );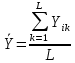
       
     • 
       S2Y – дисперсия скоростей ( );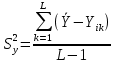
       
     • 
       Gmax, S2vos, S2ost, Fish, k – для дальнейших расчетов;
       

• 
  таблица сохранена по маршруту «E:\kurs2\gr2-21\KM\» с именем КМ2-21.sta
  

3. Оценка качества выполненного эксперимента

Расчет дисперсий и их анализ был выполнен в статистическом модуле Descriptive Statistics. Полученные результаты:



Расчетный критерий Кохрена: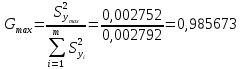



Табличный критерий Кохрена

• 
  степени свободы – 𝑓₁ = 𝐿 − 1 = 3 − 1 = 2; 𝑓₂ = 𝑚 = 30;
  
• 
  𝐺_4,30 = 0,137, взято из таблицы
  

Таким образом, G_max > G_т => дисперсии неоднородны. Промахи в дальнейшем не исключали. Поэтому приняли:

• 
  дисперсия воспроизводимости: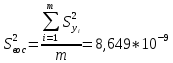
  

• 
  методику оценки коэффициентов регрессии не меняем (МНК).
  

5. Оценка тесноты связи между факторами и откликом

Получена следующая матрица: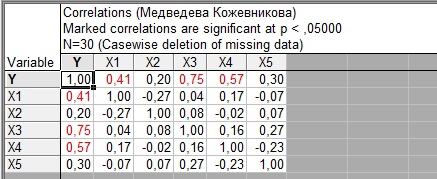

Оценка коэффициентов регрессии

Ур-е регрессии: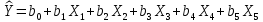

Полученные результаты: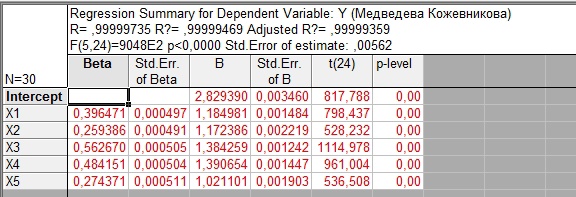



Т.о., ур-е регрессии с численными коэффициентами: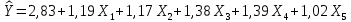


Анализ остатков и выявление выбросов

Выбросов нет

6. Проверка значимости регрессионных факторов

На основании расчетных значений уровня значимости (p-level < 0,05), корреляционной матрицы (нет корреляционных коэффициентов, близких к 0) и критерия Стьюдента ( 𝑝 = 0,05; 𝑡_таб(20) = 2,085; ^|𝑡_𝑖^| > 𝑡_таб) можно утверждать, что все коэффициенты значимы.
Остаточная дисперсия:


Проверка адекватности регрессии

Расчетный критерий Фишера:

𝐹 =

2


𝑆
ост




𝑆
2

восп

1,024*10<sup>-9

=</sup> 8,649*10^-9
= 0,1184

Табличный критерий Фишера:

𝑓₁ = 𝑚 − 𝑛 − 1 = 30 − 5 − 1 = 24; 𝑓₂ = 𝑚⁽𝐿 − 1⁾ = 30 ∗ ⁽3 − 1⁾ = 60; 𝑝 =

0,05  𝐹_таб= 1,7001

Таким образом, 𝐹 < 𝐹_таб– регрессия адекватна.

7. Обратный переход к исходному уравнению кинетики

Ур-е регрессии: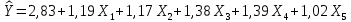


Константа скорости: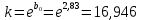

Ур-е кинетики: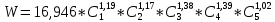

5. 
   Вывод: в ходе лабораторной работы обработали результаты кинетического эксперимента. Выяснено:
   
   • 
     дисперсии исходных опытов неоднородны;
     
   • 
     ур-е регрессии: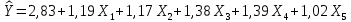
     
     
   • 
     выбросы не имеются;
     
   • 
     все факторы в уравнении регрессии значимы;
     
   • 
     регрессия адекватна;
     
   • 
     
     
     
     ур-е кинетики: ;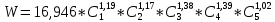
     
   • 
     полученные результаты ощутимо расходятся с ожидаемыми, т.к. не была устранена неоднородность дисперсий данных эксперимента.