Массивы и матрицы в SciLab. Лаб раб 2 Массивы и матрицы в SciLab NEW. Лабораторная работа 2 Массивы и матрицы в SciLab Цель работы изучить основы работы с множеством данных к работе допущен
 Скачать 34.82 Kb. Скачать 34.82 Kb.
|
|
Лабораторная работа №2 Массивы и матрицы в SciLab Цель работы: изучить основы работы с множеством данных К работе допущен: Работу выполнил: Работу защитил: ВВЕДЕНИЕДля работы с множеством данных удобно использовать массивы. Например, можно создать массив для хранения числовых или символьных данных. В этом случае вместо создания переменной для хранения каждого данного достаточно создать один массив, где каждому элементу будет присвоен порядковый номер. Таким образом, массив — множественный тип данных, состоящий из фиксированного числа элементов. Как и любой другой переменной, массиву должно быть присвоено имя. Переменную, представляющую собой просто список данных, называют одномерным массивом, или вектором. Для доступа к данным, хранящимся в определенном элементе массива, необходимо указать имя массива и порядковый номер этого элемента, называемый индексом. Если возникает необходимость хранения данных в виде таблиц, в формате строк и столбцов, то необходимо использовать двумерные массивы (матрицы). Для доступа к данным, хранящимся в таком массиве, необходимо указать имя массива и два индекса: первый должен соответствовать номеру строки, а второй — номеру столбца, в которых хранится необходимый элемент. Значение нижней границы индексации в Scilab равно единице. Индексы могут быть только целыми положительными числами. Ввод и формирование массивов и матриц. Один из способов задания векторов и матриц в Scilab — это их поэлементный ввод. Так, для определения вектора-строки следует ввести имя массива, а затем после знака присваивания, в квадратных скобках через пробел или запятую, перечислить элементы массива: name=[x1 x2 ... xn] или name=[x1, x2, ..., xn] Пример ввода вектора-строки: Листинг 1. Определение вектора-строки --> V=[1 2 3 4 5] V = 1 2 3 4 5 --> W=[1.1,2.3,-0.1,5.88] W = 1.1000 2.3000 -0.1000 5.8800 Элементы вектора-столбца вводятся через точку с запятой: name=[x1; x2; ...; xn] Пример ввода вектора-столбца: Листинг 2. Определение вектора-столбца --> X=[1;2;3] X = 1 2 3 Обратиться к элементу вектора можно, указав имя массива и порядковый номер элемента в круглых скобках: name(индекс) Например: Листинг 3. Пример обращения к элементу массива --> W=[1.1,2.3,-0.1,5.88]; --> W(1)+2*W(3) ans = 0.9000 Ввод элементов матрицы также осуществляется в квадратных скобках, при этом элементы строки отделяются друг от друга пробелом или запятой, а строки разделяются между собой точкой с запятой: name=[x11, x12, ..., x1n; x21, x22, ..., x2n; ...; xm1, xm2, ..., xmn;] Обратиться к элементу матрицы можно, указав после имени матрицы, в круглых скобках через запятую, номер строки и номер столбца на пересечении которых элемент расположен: name(индекс1, индекс2) Действия над матрицами. Для работы с матрицами и векторами в Scilab предусмотрены следующие операции: + — сложение; - — вычитание1; ’ — транспонирование2; * — матричное умножение3; * — умножение на число; ˆ — возведение в степень4; \ — левое деление5; / — правое деление6; .* — поэлементное умножение матриц; .ˆ — поэлементное возведение в степень; .\ — поэлементное левое деление; ./ — поэлементное правое деление. Если к некоторому заданному вектору или матрице применить математическую функцию, то результатом будет новый вектор или матрица той же размерности, но элементы будут преобразованы в соответствии с заданной функцией. Практическая частьЗадание 1(вариант 1): Решить систему линейных алгебраических уравнений, сделать проверку: 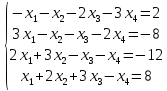 использовав программу SciLab. Выполнение: Для создания кода программы используем редактор SciNotes. Запускаем пр. SciLab → Инструменты → Текстовый редактор SciNotes. Для решения будем использовать функцию LINSOLVE (linsolve(A,b) — решает систему линейных алгебраических уравнений вида 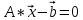 .) Так как вектор столбец свободных членов в нашей системе находится справа, а вектор столбец свободных членов функции LINSOLVE находится слева, => свободные члены в нашей системе переносим влево сменив знак. .) Так как вектор столбец свободных членов в нашей системе находится справа, а вектор столбец свободных членов функции LINSOLVE находится слева, => свободные члены в нашей системе переносим влево сменив знак.Для того, чтобы решить систему линейных алгебраических уравнений необходимо выписать матрицу коэффициентов при “x” и вектор столбец свободных членов. Листинг 4. Определение матрицы A = (-1,-1,-2,-3;3,-1,-1,-2;2,3,-1,-1;1,2,3,-1) b = -(2;-8;-12;8) Получаем решение с помощью функции LINSOLVE. Листинг 5. Решение A = (-1,-1,-2,-3;3,-1,-1,-2;2,3,-1,-1;1,2,3,-1) b = (2;-8;-12;8) x = linsolve(A,b) Выполним проверку, получив решение другим способом. Выводим решение в консоль. Функция «inv(A)» — вычисляет матрицу, обратную к «A». Обратной матрицей по отношению к данной называется матрица того же типа, которая будучи умноженной как слева, так и справа на данную матрицу, в результате даст единичную матрицу. Т.е. при умножении А на inv(A) слева должна получиться единичная матрица. Листинг 6. Проверка и вывод A = [-1,-1,-2,-3;3,-1,-1,-2;2,3,-1,-1;1,2,3,-1] b = [2;-8;-12;8] x = linsolve(A,-b) x_inv = inv(A)*b disp(x,"Решение системы: ") disp(x_inv,"Проверка решения системы: ") Листинг 7. Результат выполнения кода программы в SciLab Решение системы: - 3.0196078 - 1.2941176 3.9215686 - 1.8431373 Проверка решения системы: - 3.0196078 - 1.2941176 3.9215686 - 1.8431373 Задание 1.2 (вариант 1). Если возможно, вычислить матрицу, обратную к матрице D. 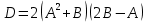 , где , где 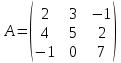 , B= , B=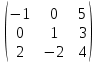 использовав программу SciLab. Выполнение: Для создания кода программы используем редактор SciNotes. Запускаем пр. SciLab → Инструменты → Текстовый редактор SciNotes. Для того, чтобы посчитать матрицу «D» определяем матрицы «A» и «B» Листинг 8. Определение матриц «A» и «B» A=[2,3,-1;4,5,2;-1,0,7] B=[-1,0,5;0,1,3;2,-2,4] Считаем матрицу «D» Листинг 9. Ввод формулы матрицы «D» A=[2,3,-1;4,5,2;-1,0,7] B=[-1,0,5;0,1,3;2,-2,4] D=2*(A^2+B)*(2*B-A) Листинг 10. Посчитаем матрицу обратную к матрице «D» A=[2,3,-1;4,5,2;-1,0,7] B=[-1,0,5;0,1,3;2,-2,4] D=2*(A^2+B)*(2*B-A) invD = inv(D) Листинг 11. Выводим на экран матрицу «D» и матрицу обратную к матрице «D» A=[2,3,-1;4,5,2;-1,0,7] B=[-1,0,5;0,1,3;2,-2,4] D=2*(A^2+B)*(2*B-A) invD = inv(D) disp(D,"Матрица D:") disp(invD,"Матрица, обратная к D:") Листинг 12. Результат выполнения кода программы в SciLab Матрица D: - 276. - 238. 524. - 282. - 568. 922. 636. - 360. - 86. Матрица, обратная к D: 0.1055009 - 0.0579384 0.0216661 0.1557544 - 0.0857622 0.0295649 0.1282210 - 0.0694702 0.0248402 ВЫВОДВ ходе лабораторной работы познакомились с возможностью работы с массивами и матрицами в программе SciLab. Для необходимых вычислений использовали функции «LINSOLVE» (решает систему линейных алгебраических уравнений вида 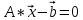 ) и «inv(A)» (вычисляет матрицу, обратную к матрице «A»). ) и «inv(A)» (вычисляет матрицу, обратную к матрице «A»). |
