кк. Лабораторная работа 2 (2). Лабораторная работа 2 Обработка матриц и векторов
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
Лабораторная работа №2 Обработка матриц и векторов Цель: приобретение навыков работы в рабочем окне пакета MATLAB: изучение способов формирования матриц, векторов, подматриц. Раздел 1: Матрицы Задание 1: Одно число, называемое скаляром, на самом деле является массивом 1 на 1, что означает, что оно содержит 1 строку и 1 столбец. ЗАДАЧА Создайте переменную с именем x со значением 4. Задание 2: Вы можете создавать массивы из нескольких элементов, используя квадратные скобки. х = [3 5] х = 3 5 ЗАДАЧА Создайте массив с именем x с двумя элементами: 7 и 9 Задание 3: Когда вы разделяете числа пробелами (или запятыми), как показано в предыдущей задаче, MATLAB объединяет числа в вектор-строку, который представляет собой массив с одной строкой и несколькими столбцами (1 на n). Когда вы разделяете числа точкой с запятой, MATLAB создает вектор-столбец (n-на-1). х = [1; 3] х = 1 3 ЗАДАЧА Создайте массив с именем x с двумя элементами, 7 и 9, в одном столбце. Попробуйте скопировать предыдущую команду и заменить пробел между числами точкой с запятой (;). Задание 4: Создайте вектор-строку с именем x, который содержит значения 3, 10 и 5 в указанном порядке. Задание 5: Создайте вектор-столбец с именем x, который содержит значения 8, 2 и -4 в указанном порядке. Задание 6: Вы можете комбинировать пробелы и точки с запятой для создания матрицы, которая представляет собой массив с несколькими строками и столбцами. При вводе матрицы вы должны вводить их построчно. x = [3 4 5; 6 7 8] х = 3 4 5 6 7 8 ЗАДАЧА Создайте матрицу с именем x со значениями, показанными ниже. 5 6 7 8 9 10 Задание 7: В MATLAB вы можете выполнять вычисления в квадратных скобках. х = [abs (-4) 4 ^ 2] х = 4 16 ЗАДАЧА Создайте вектор-строку с именем x, который содержит sqrt (10) в качестве первого элемента и pi ^ 2 (π2) в качестве второго элемента. Раздел 2: Создание равномерно разнесенных векторов Задание 1: Обычно создаются векторы, содержащие числа с равным интервалом, такие как вектор ниже. y = [5 6 7 8] y = 5 6 7 8 ЗАДАЧА Создайте вектор-строку с именем x, который содержит значения 1, 2 и 3 в указанном порядке. Задание 2: Для длинных векторов ввод отдельных чисел нецелесообразен. Альтернативный сокращенный метод создания равномерно распределенных векторов - использовать оператор: и указать только начальную и конечную точки. у = 5: 8 y = 5 6 7 8 Обратите внимание, что квадратные скобки не нужны при использовании оператора двоеточия. ЗАДАЧА Создайте вектор-строку с именем x со значениями 1, 2, 3 и 4, но на этот раз с помощью оператора:. Задание 3: Оператор: использует интервал по умолчанию 1, однако вы можете указать свой собственный интервал, как показано ниже. х = 20: 2: 26 х = 20 22 24 26 ЗАДАЧА Создайте вектор-строку с именем x, который начинается с 1, заканчивается 5, и каждый элемент отделен 0,5. Задание 4: Создайте вектор-строку с именем x, который начинается с 3 и заканчивается 13, шаг между элементами равен 2. Задание 5: Если вы знаете количество элементов, которые хотите в векторе (а не расстояние между каждым элементом), вы можете вместо этого использовать функцию linspace: linspace (первый, последний, число_элементов). Обратите внимание на использование запятых (,) для разделения входных данных в функцию linspace. x = linspace (0,1,5) х = 0 0.250 0.500 0.750 1.000 ЗАДАЧА Создайте вектор-строку с именем x, который начинается с 1, заканчивается 10 и содержит 5 элементов. Задание 6: И linspace, и оператор : создают векторы-строки. Однако вы можете преобразовать вектор-строку в вектор-столбец с помощью оператора транспонирования ('). х = 1 : 3; х = х ' х = 1 2 3 ЗАДАЧА Транспонируйте x из вектора-строки в вектор-столбец с помощью оператора транспонирования. Задание 7: Вы можете создать векторы-столбцы с помощью одной команды, создав вектор-строку и переставив все это в одну строку. Обратите внимание на использование здесь круглых скобок для указания порядка операций. х = (1: 2: 5) ' х = 1 3 5 ЗАДАЧА В одной команде создайте вектор-столбец с именем x, который начинается с 5, заканчивается 9 и имеет элементы, разделенные интервалом 2. Раздел 3: Функции создания массива Задание 1: MATLAB содержит множество функций, которые помогут вам создавать часто используемые матрицы, такие как матрицы случайных чисел. х = rand (2) х = 0.8147 0.1270 0.9058 0.9134 Обратите внимание, что 2 в команде rand (2) указывает, что на выходе будет матрица случайных чисел 2 на 2. ЗАДАЧА Создайте переменную с именем x, которая представляет собой матрицу случайных чисел 5 на 5. Задание 2: Многие функции создания матриц позволяют ввести одно число для создания квадратной матрицы (n на n) или ввести два числа для создания неквадратных матриц. х = rand (2) х = 0.8147 0.1270 0.9058 0.9134 х = rand (2,3) х = 0.6324 0.2785 0.9575 0.0975 0.5469 0.9649 ЗАДАЧА Используйте rand для создания массива, содержащего 5 строк и 1 столбец. Назначьте результат переменной с именем x. Задание 3: Большинство функций создания массивов принимают те же входные данные, что и rand. Например, функции нулей – zeros и единиц – ones создают матрицы всех нулей или единиц соответственно. х = ones (2,3) х = 1 1 1 1 1 1 ЗАДАЧА Используйте функцию нулей, чтобы создать матрицу всех нулей, которая имеет 6 строк и 3 столбца (6 на 3). Назначьте результат переменной с именем x. Раздел 4: Индексирование и изменение массивов Задание 1: Создайте случайный массив data из 7 строк и 3 столбцов Задание 2: Вы можете извлекать значения из массива, используя индексирование строк и столбцов. у = А (5,7) Этот синтаксис извлекает значение в 5-й строке и 7-м столбце массива A и присваивает результат переменной y. ЗАДАЧА Создайте переменную x, которая содержит значение в 6-й строке и 3-м столбце переменной data. Задание 3: Вы можете использовать ключевое слово end в MATLAB как индекс строки или столбца для ссылки на последний элемент. у = А (end, 2) ЗАДАЧА Используйте ключевое слово end, чтобы получить значение в последней строке и 3-м столбце переменной data. Присвойте это значение переменной с именем x. Задание 3: Обратите внимание, что вы можете использовать арифметику с ключевым словом end. Например: y = A (end-1, end-2) ЗАДАЧА Создайте скалярную переменную x, которая содержит значение из предпоследней строки и 3-го столбца данных. Задание 4: При использовании в качестве индекса оператор двоеточия (:) указывает все элементы в этом измерении. Синтаксис х = А (2, :) создает вектор-строку, содержащий все элементы из второй строки A. ЗАДАЧА Создайте переменную с именем density, которая содержит второй столбец матрицы с именем data. Задание 5: Оператор двоеточия может относиться к диапазону значений. Следующий синтаксис создает матрицу, содержащую первую, вторую и третью строки матрицы A. х = А (1: 3, :) ЗАДАЧА Создайте переменную volumes, содержащие два последних столбца данных. Задание 6: Одно значение индекса может использоваться для ссылки на векторные элементы. Например х = v (3) возвращает третий элемент вектора v, если v является вектором-строкой или вектор-столбцом. ЗАДАЧА Используя одно значение индекса, создайте переменную с именем p, содержащую шестой элемент density. Задание 7: Один диапазон значений индекса может использоваться для ссылки на подмножество элементов вектора. Например х = v (3: end) возвращает подмножество вектора v, содержащее элементы от 3 до конца. ЗАДАЧА Используя диапазон значений индекса, создайте вектор с именем p, содержащий элементы со 2-го по 5-й density. Раздел 5: Изменение значений в массивах Задание 1: Помните, что вы можете использовать символ: для извлечения целых столбцов данных. ЗАДАЧА Создайте вектор с именем v2, содержащий последний столбец data. Задание 2: Элементы переменной можно изменить, комбинируя индексирование с присваиванием. А(2) = 11 ЗАДАЧА Измените первый элемент в v2 на 0,5. Задание 3: Измените значение элемента в первой строке и последнем столбце массива data на 0,5. Раздел 6: Выполнение операций с массивами над векторами Создайте произвольные массивы mas и mas2 одинакового размера (3х3). Задание 1: Вы можете добавить скалярное значение ко всем элементам массива. х = [1 2 3]; у = х + 2 y = 3 4 5 ЗАДАЧА Добавьте 1 к каждому элементу mas и сохраните результат в переменной с именем mas1. Задание 2: Вы можете сложить два любых массива одинакового размера. г = х + у ЗАДАЧА Создайте вектор mas_sum, который представляет собой сумму векторов mas1 и mas2. Задание 3: Вы можете умножить или разделить все элементы массива на скаляр. г = 2 * х у = х / 3 ЗАДАЧА Создайте переменную mas_avr, которая содержит значение mas_sum, разделенное на 2. Задание 4: Максимальное значение матрицы можно определить с помощью функции max. xMax = маx (x) ЗАДАЧА Создайте переменную mas_max, содержащую максимум вектора mas_avr. Задание 5: MATLAB имеет функции, которые выполняют математические операции со всем вектором или массивом значений в одной команде. xSqrt = sqrt (х) ЗАДАЧА Используя функцию round, создайте переменную с именем massr, которая содержит округленные значения, mass_avr. Раздел 7: Вызов нескольких выходных данных Задание 1: Функцию size можно применить к массиву для создания единственной выходной переменной, содержащей размер массива. s = size (x) ЗАДАЧА Создайте переменную с именем msize, содержащую размер переменной mass_avr. Задание 2: Функцию размера можно применить к матрице для получения либо одной выходной переменной, либо двух выходных переменных. Используйте квадратные скобки ([ ]), чтобы получить более одного выходного значения. [xrow, xcol] = size (x) ЗАДАЧА Создайте переменные dr и dc, которые соответственно содержат количество строк и столбцов переменной mass_avr. Задание 3: Максимальное значение вектора и соответствующее ему значение индекса можно определить с помощью функции max. Первый вывод функции max - это максимальное значение входного вектора. При вызове с двумя выходами второй выход является значением индекса. [xMax, idx] = max (x) ЗАДАЧА Создайте переменную v2, в которую занесите 1 столбец массива mass_avr. Создайте переменные vMax и ivMax, содержащие максимальное значение вектора v2 и соответствующее значение индекса соответственно. Задание на самостоятельную работу 1. В рабочем окне MATLAB ввести матрицу А. 2. Выделить из матрицы А подматрицу В. 3. Выделить из матрицы А подматрицу С. 4. Извлечь из матрицы А диагональ D. 5. Умножить матрицу В на матрицу С с точкой и без точки. 6. Разделить матрицу В на матрицу С левым делением с точкой и без точки. 7. Разделить матрицу В на матрицу С правым делением с точкой и без точки. 8. Транспонировать матрицу А. 9. Сохранить переменные А,В, С,D в mat-файле. 10. Очистить рабочую область. Очистить экран. Загрузить сохраненные переменные в рабочую область. Вывести список переменных.
Приложение Основные команды для работы с матрицами и векторами Операторы умножения «.*» и правого деления «./» с точкой используются при перемножении или делении массивов (каждое число первого массива умножается/делится на соответствующее число второго массива). Операторы умножения и правого деления без точки применяются при перемножении или делении матриц по правилам линейной алгебры. При применении оператора левого деления с точкой «.\» и оператора без точки «\» выполняется решение систем линейных уравнений вида АХ=В по методу наименьших квадратов для матриц и векторов. При транспонировании массива (операция «.'») строки просто заменяются столбцами. При транспонировании матрицы (операция «‘» без точки) результатом является транспонированная матрица, для комплексных чисел выполняется операция комплексного сопряжения. C помощью команды diag возможно формировать или извлекать диагонали матрицы. Функция X=diag(v) формирует квадратную матрицу X с вектором v на главной диагонали; Функция X=diag(v,k) формирует квадратную матрицу X порядка length(v)+abs(k) с вектором v на k-той диагонали. Функция v=diag(X,k) извлекает из матрицы X диагональ с номером к; при к>0 - это номер к-й верхней диагонали, при к<0 - это номер к-й нижней диагонали. Функция B=reshape(A,m,n) возвращает матрицу размером [от х и], сформированную из элементов матрицы А путем их последовательной выборки по столбцам. Обращение к элементам массива происходит через оператор – круглые скобки ( ) 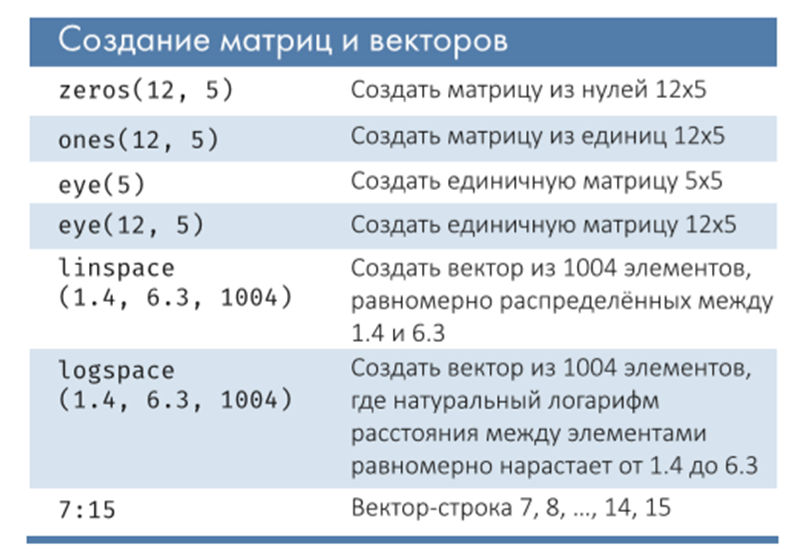 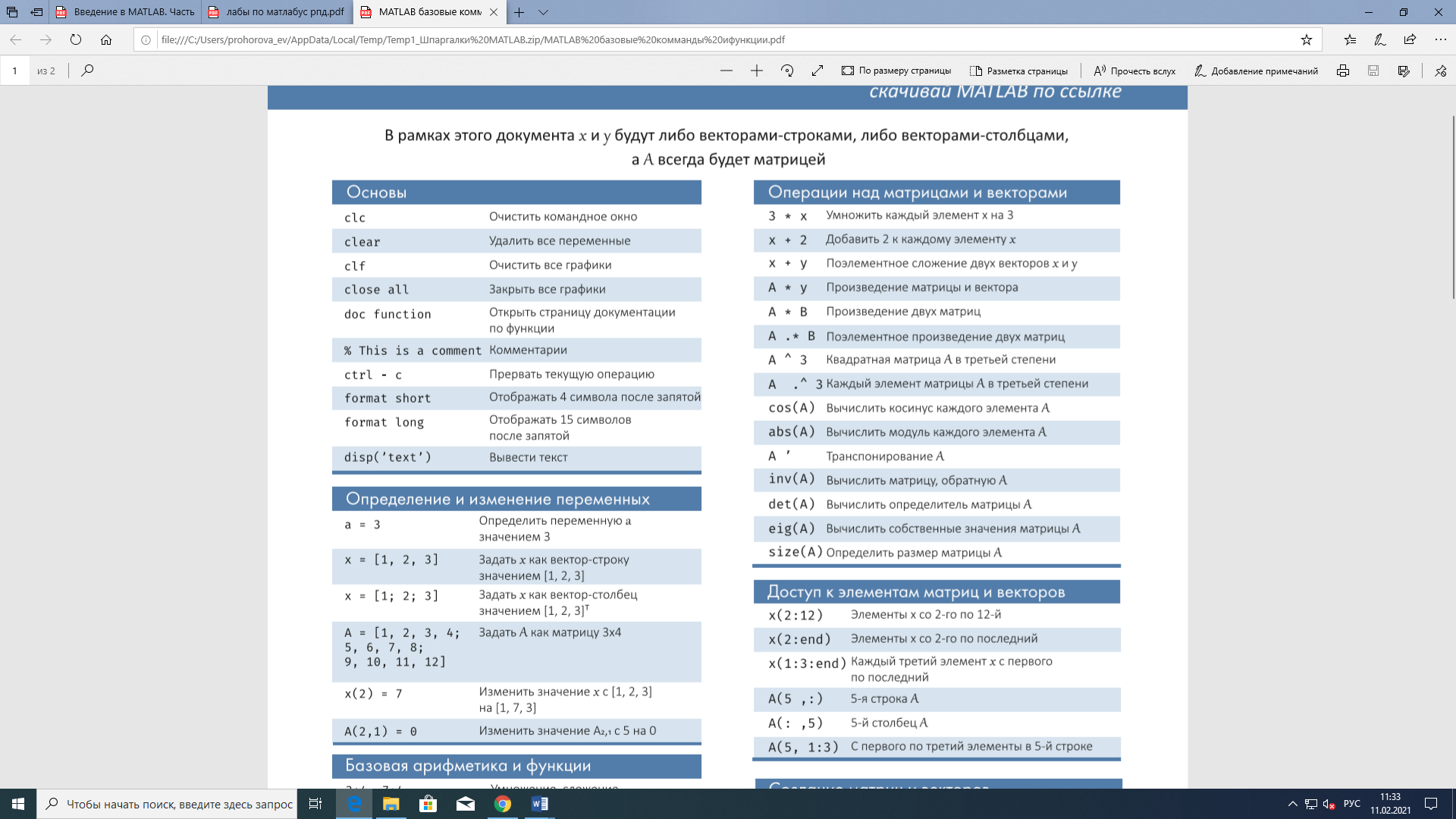 |
