Дискретная математика. Лаба №2 Дискр матемм. Лабораторная работа 2 по дисциплине Дискретная математика вариант 11 Задание 1
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
|
учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра компьютерных систем в управлении и проектировании (КСУП) ОТЧЕТ Лабораторная работа № 2 по дисциплине «Дискретная математика» вариант 11 Задание 1. Решить задачу нахождения кратчайшего маршрута на взвешенном графе с помощью алгоритма Дейкстры. Исходные данные: вершина х0 – начальная; вершина х7 – конечная. r[0,1] = 12 r[4,7] = 34 r[6,3] = 13 r[5,7] = 43 r[0,2] = 10 r[4,2] = 18 r[6,7] = 35 r[5,4] = 46 r[0,3] = 29 r[2,5] = 21 r[2,1] = 3 r[6,5] = 11 r[1,4] = 25 r[2,6] = 15 r[3,2] = 32 Построим граф (рис.1) 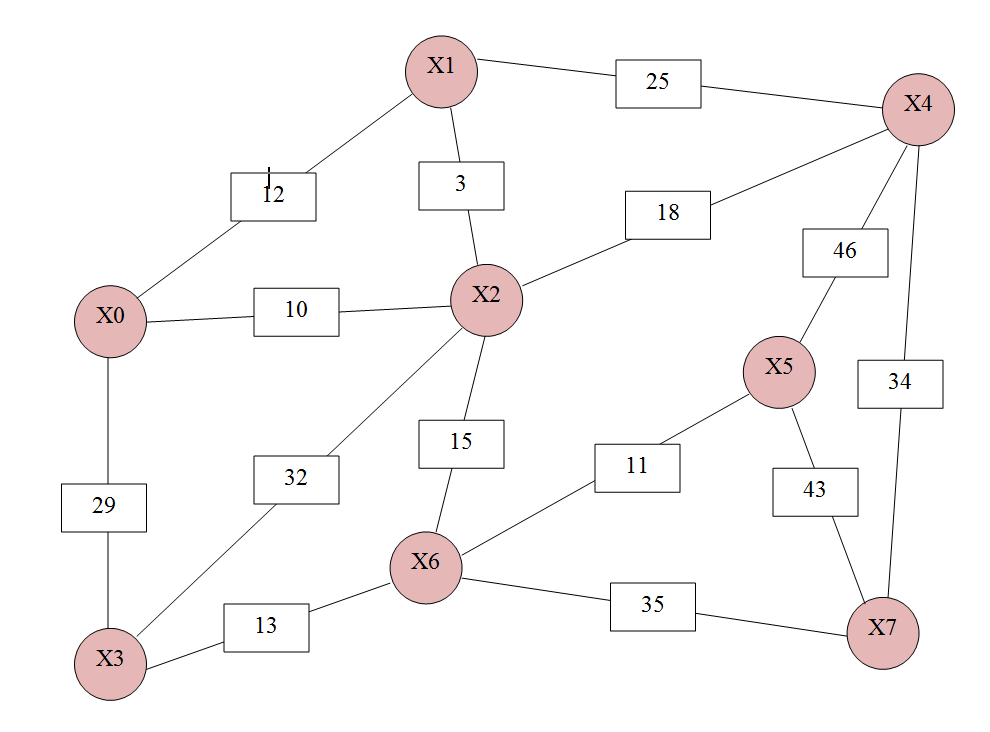 За текущую рассматриваемую вершину с постоянной пометкой возьмем вершину X0 Присвоим L(X0)=0 L(Xi)= 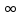 (рис.2) (рис.2)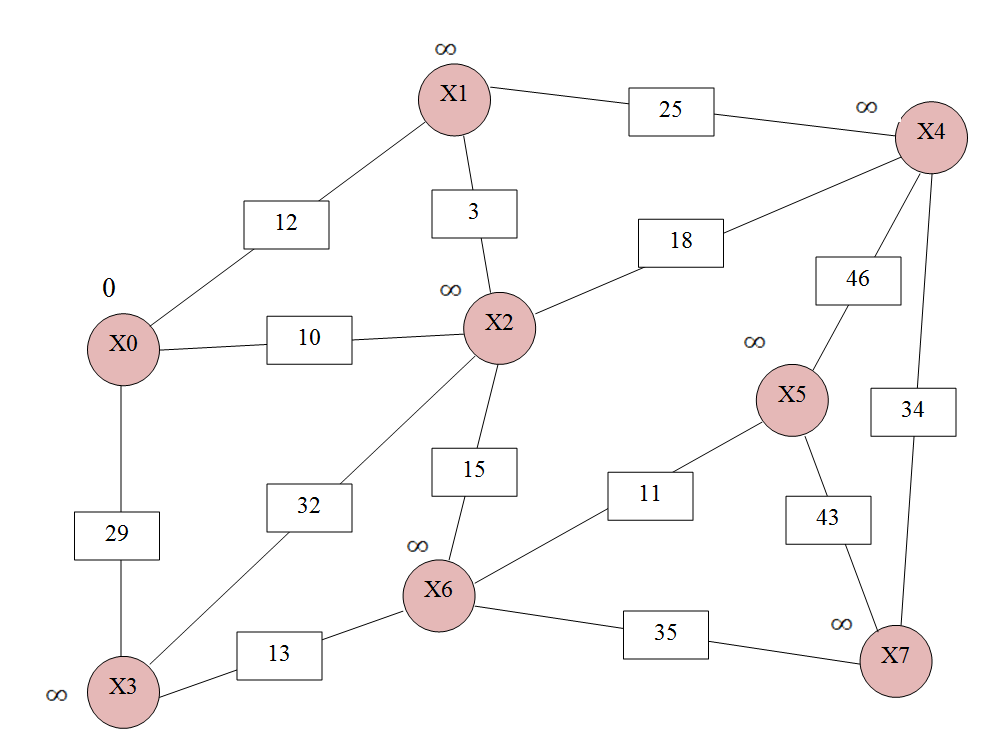 Найдем прямое отображение для текущей рассматриваемой вершины X0 это будут вершины X1, X2 X3. Все вершины, входящие в прямое отображение имеют временные пометки, поэтому пересчитаем их значение: L(X1)min( L(X2)min( L(X3)min( Имеем следующие метки вершин: L(X1)=12 L(X5)= L(X2)=10 L(X6)= L(X3)=29 L(X7)= L(X4)= Очевидно, что минимальную метку, равную 10, имеет вершина X2. За следующую текущую метку принимаем вершину X2, а метка X0 становится постоянной (рис 3). 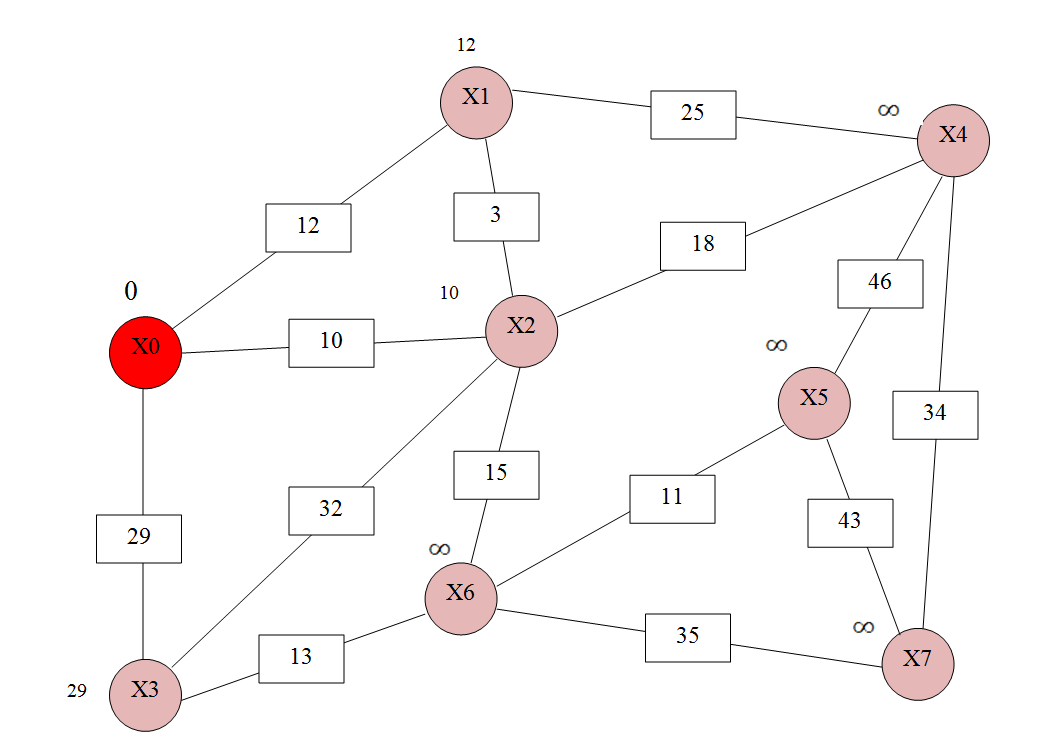 Найдем прямое отображение для текущей рассматриваемой вершины X2 это будут вершины X0, X1, X6 X3 X4. Все вершины, кроме X0, входящие в прямое отображение имеют временные пометки, поэтому пересчитаем их значение: L(X1)min(  ; 10+3)=12 оставляем метку ; 10+3)=12 оставляем меткуL(X4)min( L(X3)min( L(X6)min( Имеем следующие метки вершин: L(X1)=12 L(X3)=29 L(X4)= L(X6)= L(X5)= L(X7)= 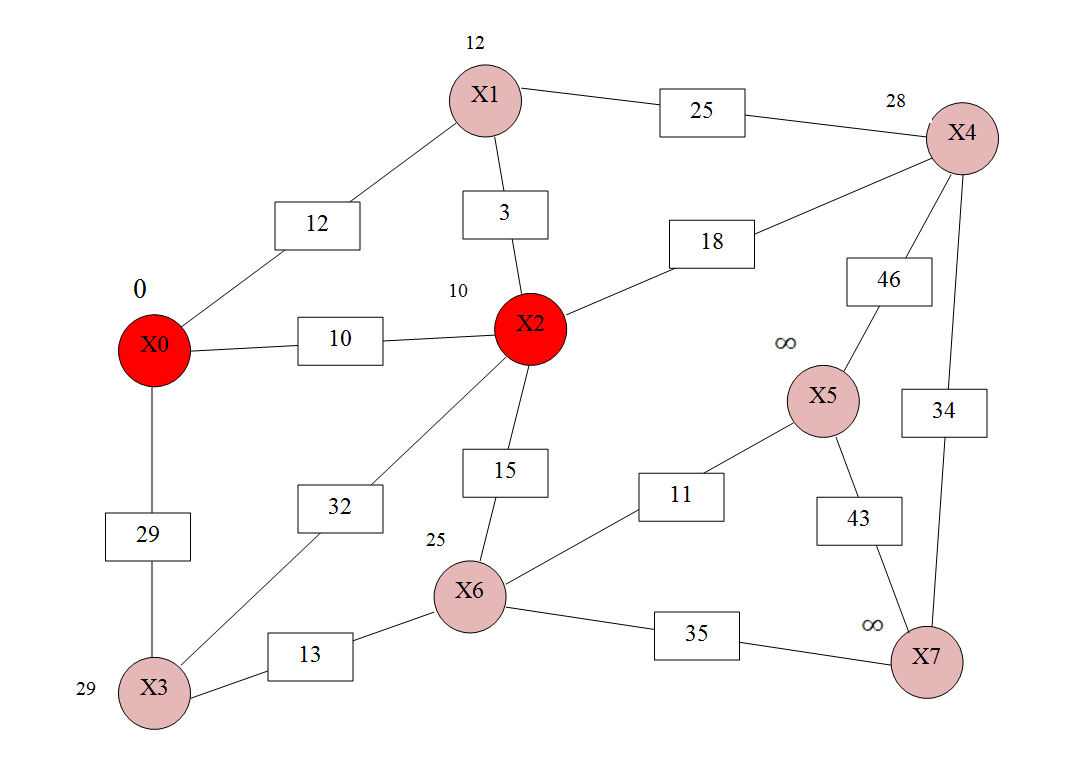 Помечаем Х2 как рассмотренную (рис.4). Найдем прямое отображение для текущей рассматриваемой вершины X1, это будут вершины X0, X2,X4. Для X0, X2 метки постоянные. Для X4 временные метки поэтому рассчитаем L(X4)min( 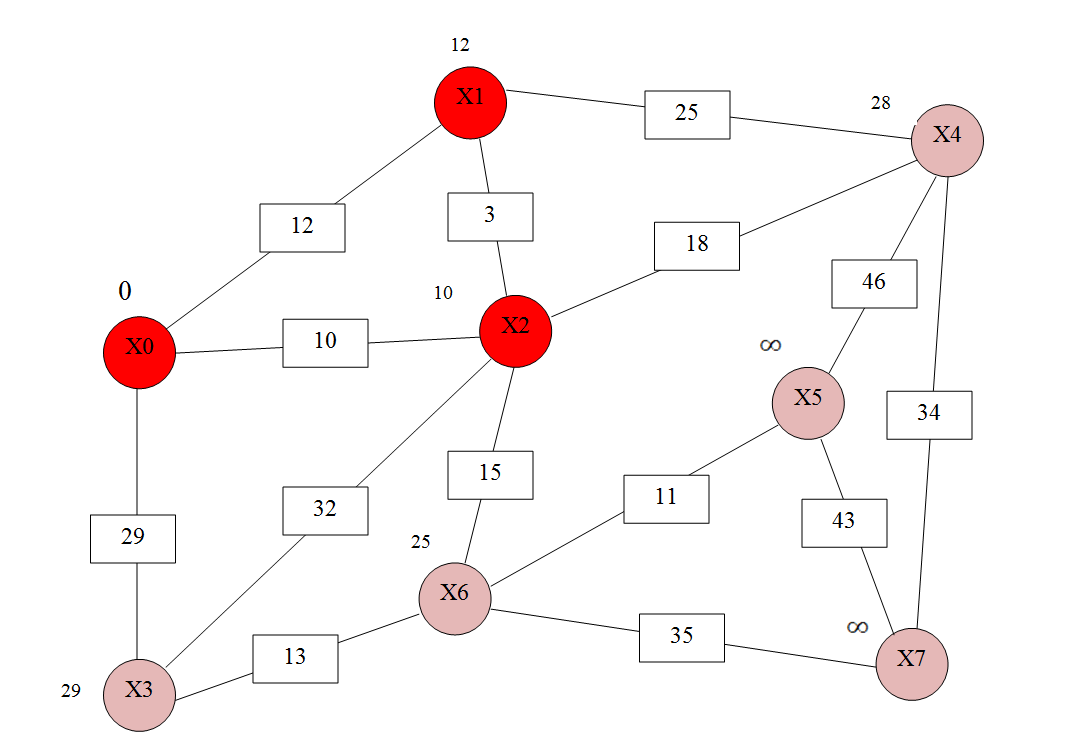 Рис.5 Перейдем к вершине X3. Найдем прямое отображение для текущей рассматриваемой вершины X3,: X0, X2,X6. Для X0, X2 метки постоянные. Для X6 временные метки поэтому рассчитаем L(X6)min( Имеем следующие временные метки L(X3)=29 L(X4)= L(X6)= L(X5)= Помечаем X3 как рассмотренную (рис.6) 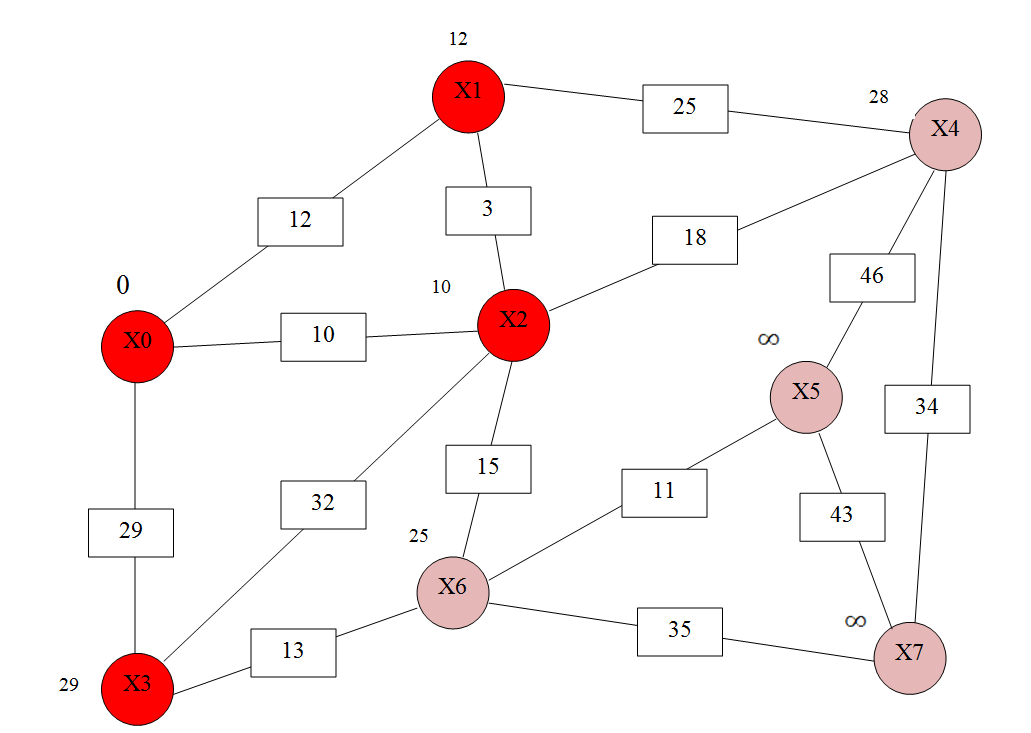 Рис.6 Перейдем к вершине X6 Найдем прямое отображение для текущей рассматриваемой вершины X6, это будут вершины X2, X3,X5 X7 Для X3, X2 метки постоянные. Для X5, X7 рассчитаем их значения. L(X5)min( L(X7)min( Имеем следующие временные метки L(X5)= 36 L(X7)= L(X4)= Все смежные вершины рассмотрены помечаем вершину X6 как рассмотренную (рис.7) 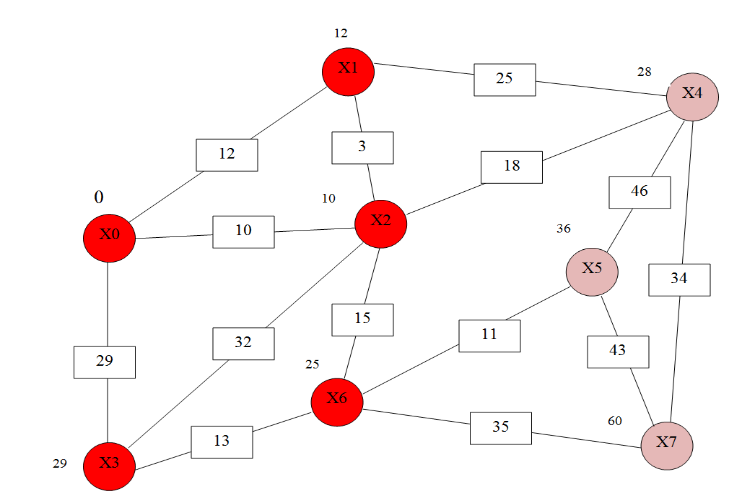 Рис.7. Перейдем к вершине X5. Найдем прямое отображение для текущей рассматриваемой вершины X5 это буду вершины X4,X6, X7 Для X6 метка постоянная. Для X4, X7 рассчитаем их значения. L(X4)min( L(X7)min( L(X4)= L(X5)= L(X7)= Все вершины рассмотрены, помечаем оставшиеся вершины: X4,X5, X7, как рассмотренные (рис.8) 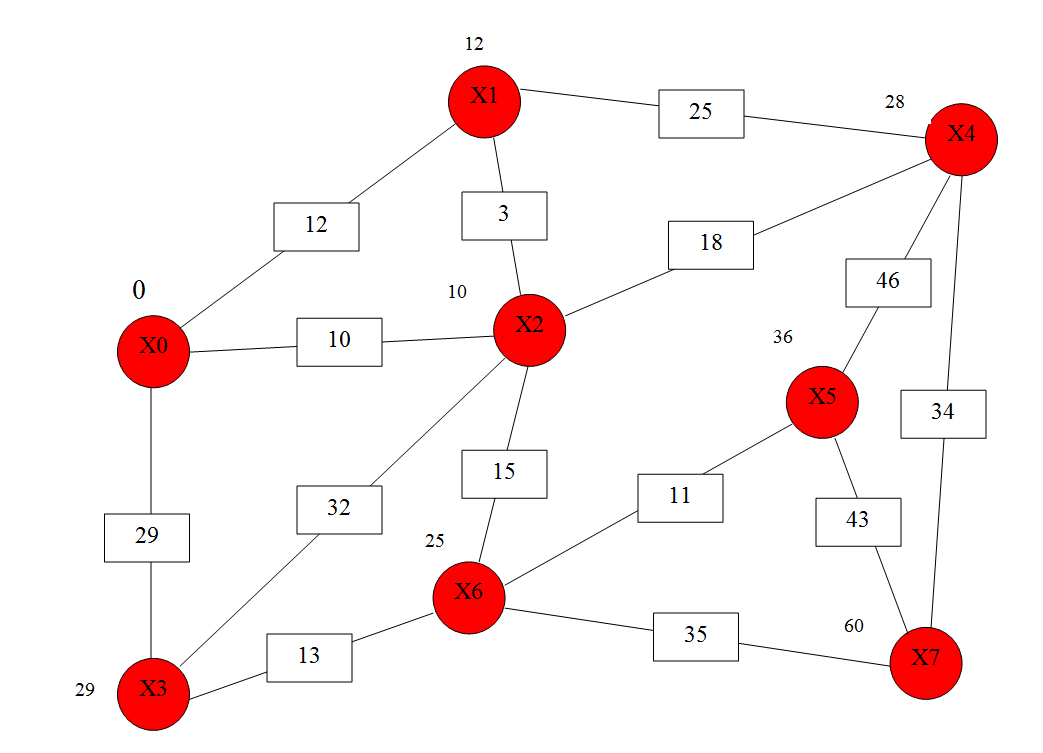 Рис.8 Все вершины имеют постоянные метки, алгоритм окончен. Для нахождения кратчайшего пути между вершинами X0 и X7. Для построения кротчайшего маршрута пройдем обратный путь от X7 к X0. X7 последовательно используем соотношение L(x*i)+c( x*i, xi)=L( xi), где L( xi) - пометка рассматриваемой вершины , L(x*i) - пометка предшествующей вершины вершине xi, с - вес ребра соединяющий вершины x*i и вершину хi ,). L(X7)=60 L(X5)+c(X5, X7)=36+43  L(X7) L(X7)L(X6)+c(X6, X7)=35+25= L(X7) Это означает, что в вершину, X7 мы попали из вершины X6. L(X6)=25 L(X3)+c(X3, X6)=13+29 L(X2)+c(X2, X6)=10+15=L(X6) В вершину, X6 мы попали из вершины X2. В свою очередь из вершины X2 мы попали из вершины X1, так как 10 минимальное значение. Ответ: кротчайший путь из X0 в X7 имеет длину 60 и проходит по вершинам: X0, X2, X6, X7. Задание 2. Решить задачу о коммивояжере. Исходные данные к задаче нахождения гамильтонова цикла в графе (задача о коммивояжере) представлены в приложении Д. Значенияэлементовматрицырасстояний: a(1.1) = a(1.2) = 95 a(2.2) = a(1.3) = 15 a(2.3) = 24 a(3.3) = a(1.4) = 13 a(2.4) = 36 a(3.4) = 18 a(4.4) = a(1.5) = 46 a(2.5) = 75 a(3.5) = 24 a(4.5) = 38 a(5.5) = Решение: Составим таблицу длин ребер
Выберем минимальный элемент в каждой строке и вычтем его из каждого элемента соответствующей строке.
Вычтем
В пятом столбце нет нуля, минимальный элемент этого столбца равен 24, вычтем его из всего столбца.
Полученная матрица содержит нули в каждом столбце и каждой строке. Попробуем по ним составить путь коммивояжера ( гамильтонов цикл) 1) Элемент (5;2)=0, убираем пятую строку и первый столбец.
2) Элемент (4;1)=0, убираем четвертую строку и пятый столбец.
3) Элемент (3;5)=0, убираем третью строку и четвертый столбец.
4) Элемент (2;3)=0, убираем вторую строку и третий столбец.
5) Остается только элемент (1;4)=0. Ответ: получили гамильтонов цикл (5;2) (4;1) (3;5) (2;3) (1;4). 13 + 24 + 24 + 11 + 3 = 75 – длина пути. Задание 3. Решить задачу нахождения максимального потока в транспортной сети с помощью алгоритма Форда – Фалкерсона. Исходные данные: Дана сеть S(X,U) x0 – исток сети; x7 – сток сети, где x0  X; x7 X; x7 Значения пропускной ri,j способности дуг сети представлены в приложении Е. Задание: 1. Вычислить значение максимального потока на сети S, применяя алгоритм Форда – Фалкерсона. 2. Построить разрез сети S. Примечание Значения пропускных способностей дуг ri,j заданы по направлению ориентации дуг: от индекса i к индексу j. ВАРИАНТ 11 [0,1] = 32 r[4,7] = 4 r[6,3] = 13 r[5,7] = 43 r[0,2] = 84 r[4,2] = 18 r[6,7] = 35 r[5,4] = 26 r[0,3] = 91 r[2,5] = 21 r[2,1] = 73 r[6,5] = 61 r[1,4] = 25 r[2,6] = 15 r[3,2] = 32
1. Зададим на сети нулевой поток (на всех дугах величина потока равна 0). Нулевой поток — это начальный допустимый поток на сети. Значение потока на каждой дуге будем указывать за скобками пропускной способности дуги.). Значение потока, равное «0», не указываем. 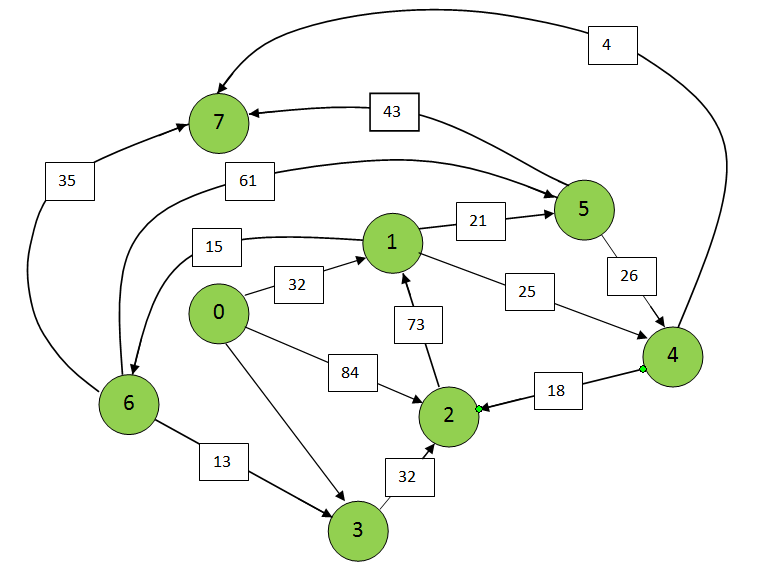 911 2. Выбираем на сети (произвольно) путь, ведущий из вершины x0 в вершину x7: X0-X1-X5-X7 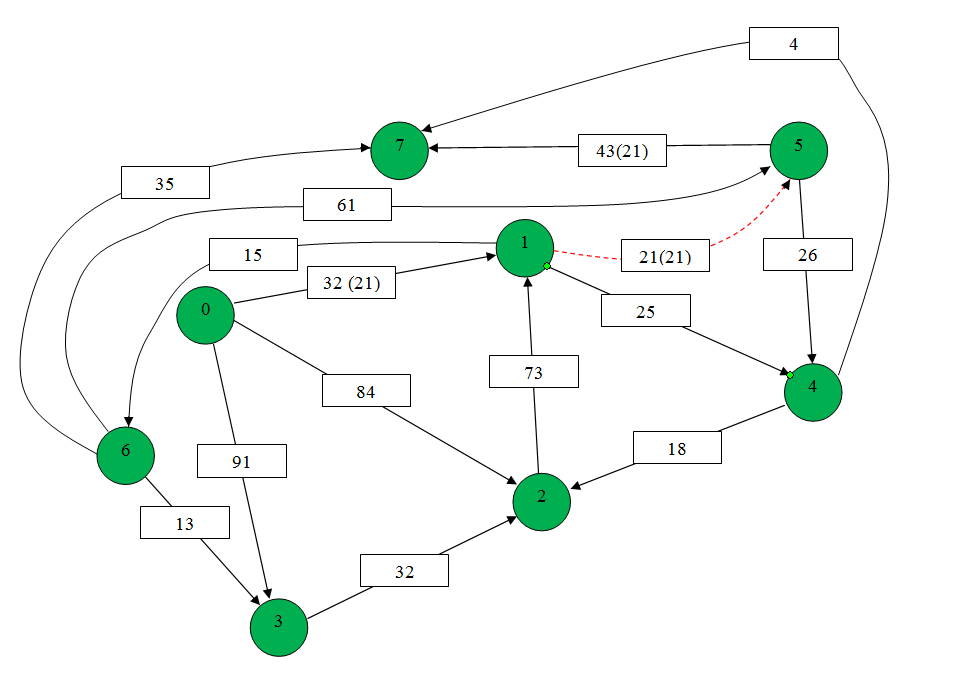 Находим min (32,21,43)=21 и увеличиваем поток на эту величину. Ребро Х1-Х5 помечаем как рассмотренное. Выбираем еще один путь, X0-X3-X2-X1-X4-X7 Находим min (91,32,73,25,4)=4 и увеличиваем поток на эту величину. Ребро Х4-Х7 помечаем как рассмотренное. 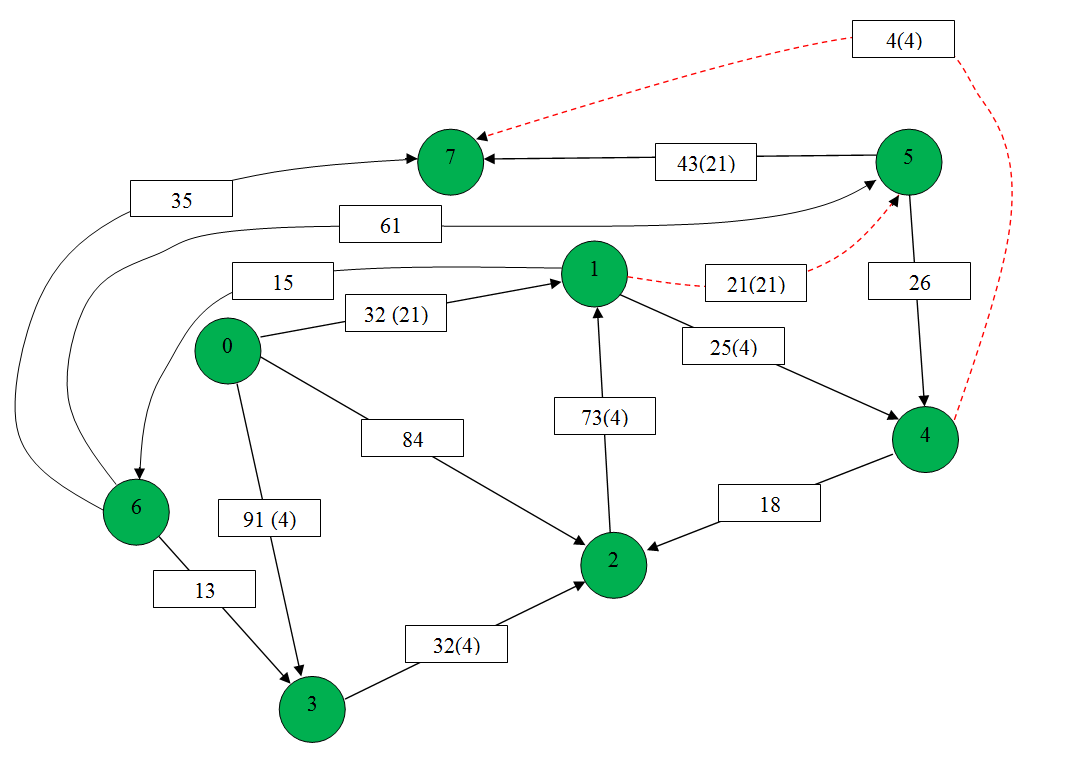 Выбираем еще один путь, X0-X1-X6-X7 Находим min (32,15,35)=15 и увеличиваем поток на эту величину. Ребро Х1-Х6 помечаем как рассмотренное 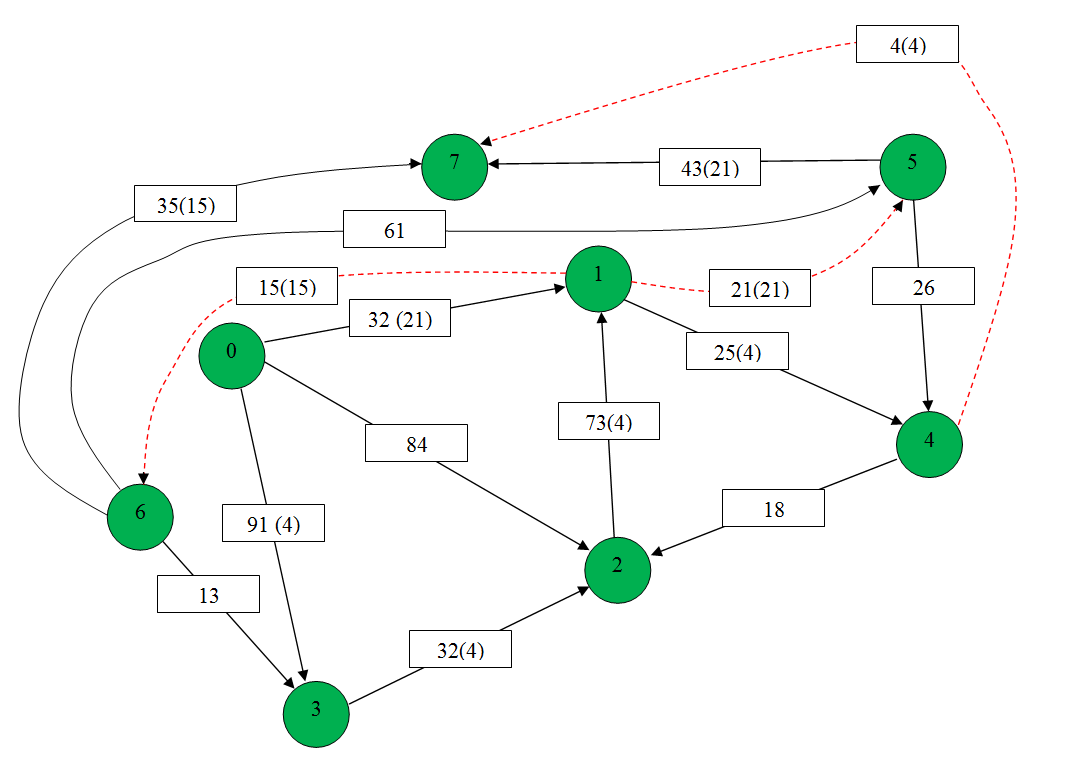 6. Более путей от Х0 до Х7 нет, суммируем увеличения потока: 21+15+4=40.Вывод: максимальный поток равен 40. Суммарный поток, заходящий в любую вершину сети(кроме истока и стока), равен суммарному потоку, выходящему из этой вершины: +(f ) = −( f) для каждой внутренней вершины x. 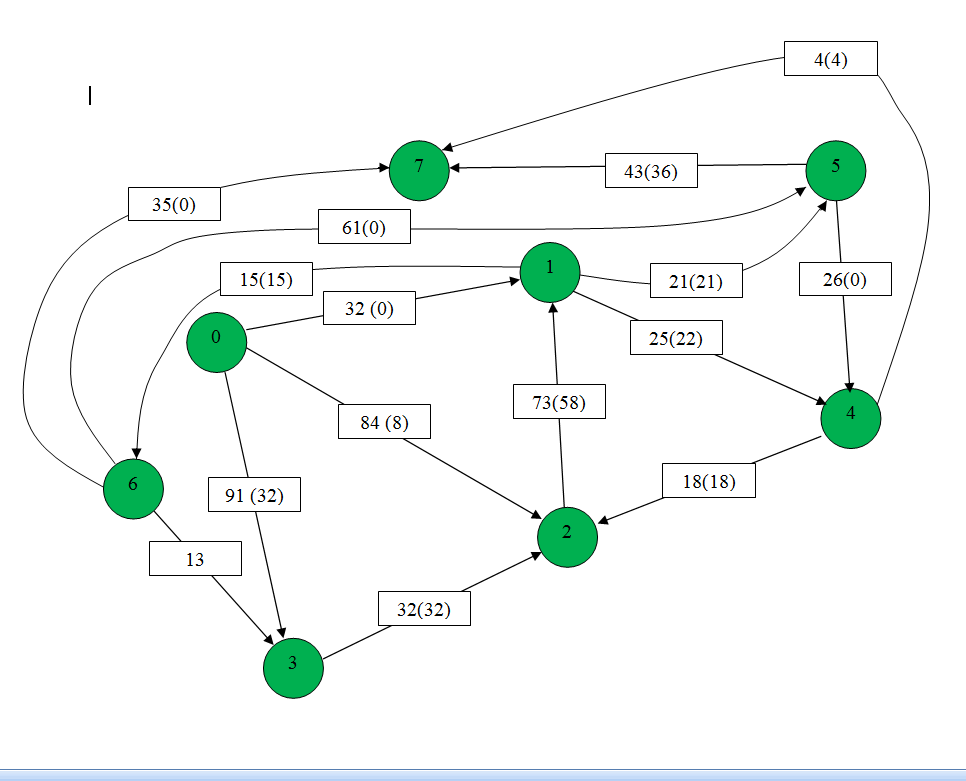 Проведем проверку баланса на насыщенной сети К примеру возьмем вершину 4 входящие 25 и 0 выходящие 4 и 8, баланс соблюден. 2) Построить разрез сети S. Процедура «пометок вершин». Начальное состояние: все вершины не имеют пометок. Вершине 0 приписывается пометка. Всем вершинам , для которых дуга не насыщена присваиваются помет (красные круги) 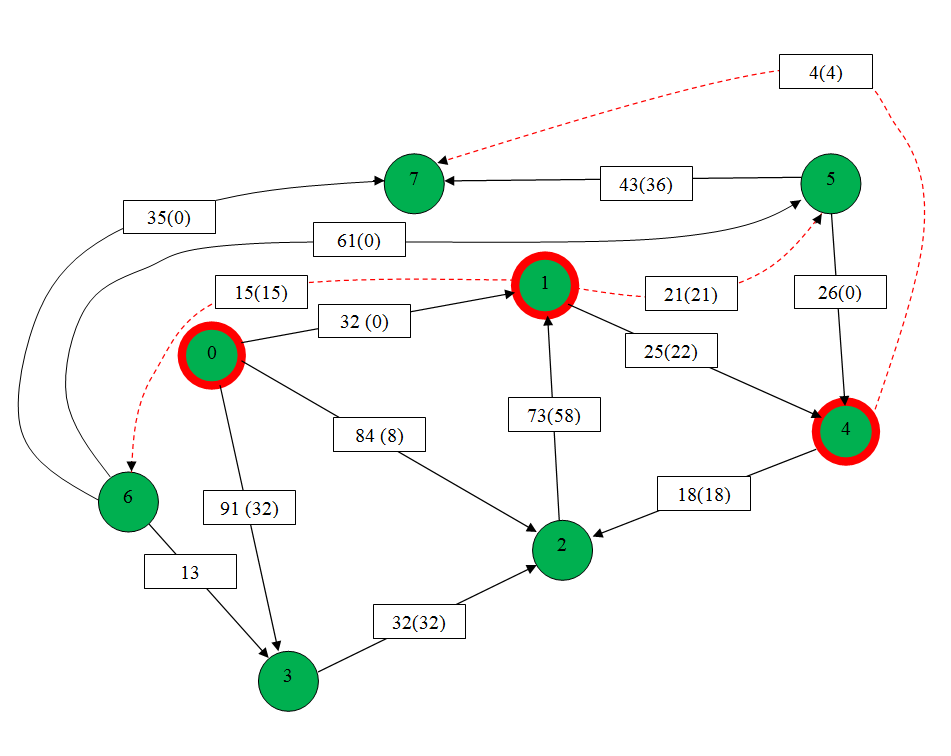 Разрезом сети называется множество дуг, удаление которых из сети приводит к тому, что исток и сток оказываются несвязанными. Определяем дуги минимального разреза: это дуги, начала которых находятся в помеченных вершинах, а концы — в непомеченных вершинах. Это дуги:U1,6 ,U1,5, U4,7 Таким образом, минимальный разрез данной сети T= (U1,6 ,U1,5, U4,7) Ответ: Фmax =40; T= (U1,6 ,U1,5, U4,7). Задание 4. Выполнить минимизацию булевой функции с помощью карты Карно. Варианты булевой функции представлены в приложении Ж. f(x,y,z) = x¬ y z ¬(x y)z x ¬(y z) x y ¬z xyz xyz. Составим таблицу истинности для данной формулы.
Построим диаграмму Карно по полученной таблице истинности, подставляя единицы в нужные ячейки.
Выделим на карте Карно прямоугольные области из единиц наибольшей площади, являющиеся степенями двойки и выпишем соответствующие им конъюнкции:
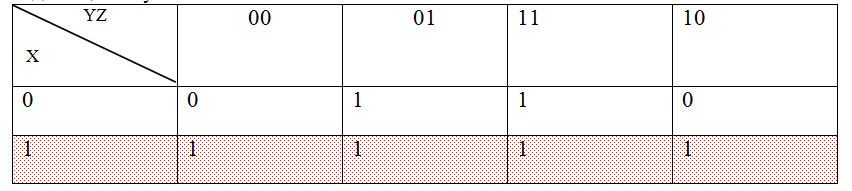 K1: x K1: x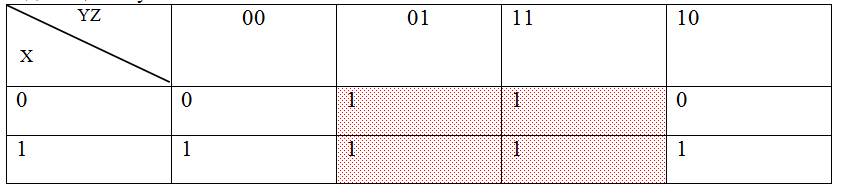 K2: z K2: zОбъединим их с помощью операции ИЛИ и получим минимизированную ДНФ: x∨z Ответ: x∨z |
