Лаб2. Лабораторная работа 2 по дисциплине Дискретная математика вариант 7 Выполнил студент группы з581П124
 Скачать 369.25 Kb. Скачать 369.25 Kb.
|
1 2 Задание 3. Решить задачу нахождения максимального потока в транспортной сети с помощью алгоритма Форда – Фалкерсона. Исходные данные: Дана сеть S (X, U) x0 – исток сети; x7 – сток сети, где x0 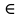 X; x7 X; x7 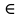 X. X.r[0,1] = 12 r[4,7] = 4 r[6,3] = 13 r[5,7] = 33 r[0,2] = 10 r[4,2] = 18 r[6,7] = 32 r[5,4] = 26 r[0,3] = 19 r[2,5] = 21 r[2,1] = 3 r[6,5] = 11 r[1,4] = 25 r[2,6] = 15 r[3,2] = 32 Задание: 1. Вычислить значение максимального потока на сети S, применяя алгоритм Форда – Фалкерсона. 2. Построить разрез сети S. Примечание Значения пропускных способностей дуг ri,j заданы по направлению ориентации дуг: от индекса i к индексу j. Решение: 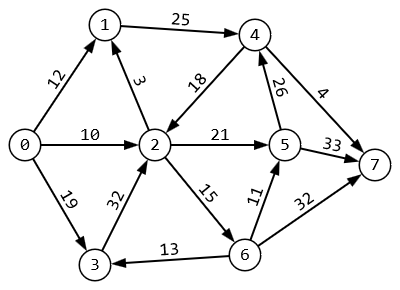 1. Зададим на сети нулевой поток (на всех дугах величина потока равна 0). Нулевой поток — это начальный допустимый поток на сети. Значение потока на каждой дуге будем указывать через дробь(/) пропускной способности дуги. Значение потока, равное «0», не указываем. 2. Выбираем на сети (произвольно) путь, ведущий из вершины x0 в вершину x7: X0-X1-X4-X7 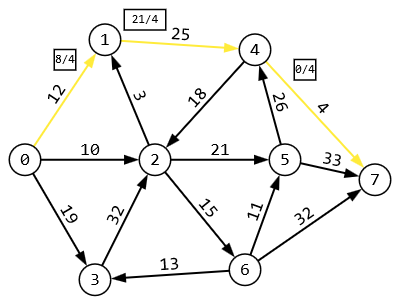 Находим min (12,25,4) =4 и увеличиваем поток на эту величину. Выбираем еще один путь, X0-X2-X6-X5-X7 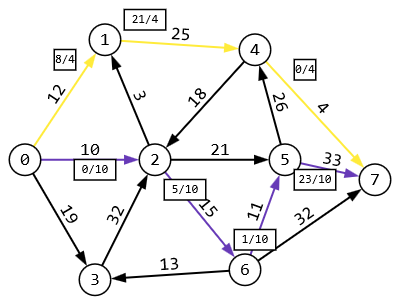 Находим min (10,15,11,33) =10 и увеличиваем поток на эту величину. Выбираем еще один путь, X0-X3-X2-X5-X7 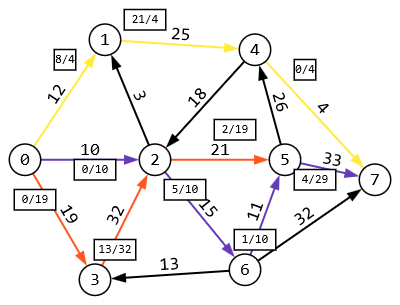 Находим min (19,32,21,23) =19 и увеличиваем поток на эту величину. Выбираем еще один путь, X0-X1-X4-X2-X6-X7 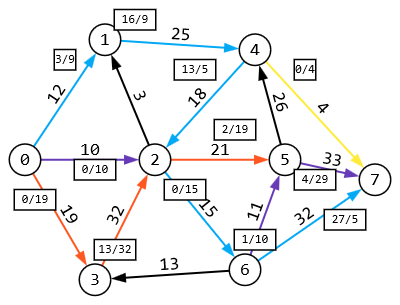 Находим min (8,21,18,5,32) =5 и увеличиваем поток на эту величину. Выбираем еще один путь, X0-X1-X4-X2-X5-X7 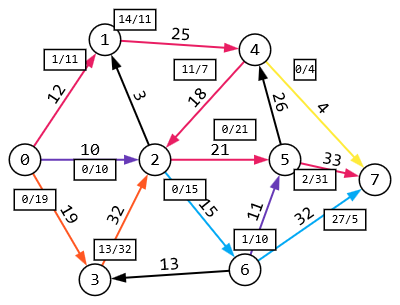 Находим min (3,16,13,2,4) =2 и увеличиваем поток на эту величину. Более путей от Х0 до Х7 нет, суммируем увеличения потока: 4+10+19+5+2=40.Вывод: максимальный поток равен 40. Суммарный поток, заходящий в любую вершину сети (кроме истока и стока), равен суммарному потоку, выходящему из этой вершины: + (f) = −(f) для каждой внутренней вершины x. Проведем проверку баланса на насыщенной сети. К примеру, возьмем вершину 6 входящее 15 выходящие 10 и 5, баланс соблюден. 2) Построить разрез сети S. Процедура «пометок вершин». Начальное состояние: все вершины не имеют пометок. Вершине 0 приписывается пометка. Всем вершинам, для которых дуга не насыщена присваиваются пометки (красный цвет) 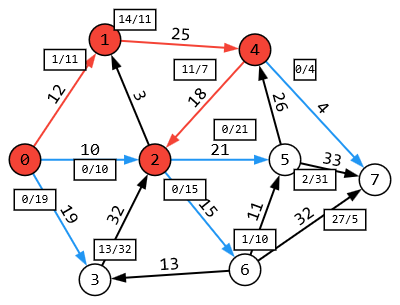 Определяем дуги минимального разреза: это дуги, начала которых находятся в помеченных вершинах, а концы — в непомеченных вершинах. 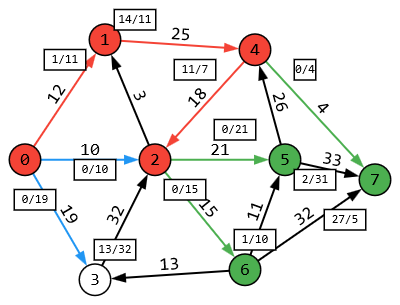 Это дуги: U2,6, U2,5, U4,7 Таким образом, минимальный разрез данной сети T= (U2,6, U2,5, U4,7) = (15+21+4) =40 Ответ: Фmax =40; T= (U2,6, U2,5, U4,7) =39 Задание 4. Выполнить минимизацию булевой функции с помощью карты Карно. f(x,y,z) = 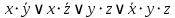 . .Составим таблицу истинности для данной формулы.
Минимизация ДНФ
Выделим на карте Карно прямоугольные области из единиц наибольшей площади, являющиеся степенями двойки и выпишем соответствующие им конъюнкции: Область 1:
K1: x Область 2:
K2: yz Объединим их с помощью операции ИЛИ и получим минимизированную ДНФ: x∨yz 1 2 |