Лаб2. Лабораторная работа 2 по дисциплине Дискретная математика вариант 7 Выполнил студент группы з581П124
 Скачать 369.25 Kb. Скачать 369.25 Kb.
|
1 2 Министерство науки и высшего образования РФ Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра компьютерных систем в управлении и проектировании (КСУП) ОТЧЕТ Лабораторная работа № 2 по дисциплине «Дискретная математика» ВАРИАНТ 7 Выполнил студент: группы з-581П12-4 направления подготовки 09.03.01 Страхова О.В. (ФИО) Проверил: к.т.н., доцент каф. КСУП ТУСУР, (ученая степень, звание) Жигалова Е. Ф. (ФИО) Томск 2022 Цель лабораторной работы Изучить алгоритм Дейкстры нахождения кратчайшего маршрута на взвешенном (нагруженном) графе, алгоритм Форда – Фалкерсона нахождения максимального потока в транспортной сети, способ минимизации булевых функций с помощью карт Карно. Задания на лабораторную работу Задание 1. Решить задачу нахождения кратчайшего маршрута на взвешенном графе с помощью алгоритма Дейкстры. Исходные данные: вершина х0 – начальная; вершина х7 – конечная. r[0,1] = 12 r[4,7] = 4 r[6,3] = 13 r[5,7] = 28 r[0,2] = 10 r[4,2] = 18 r[6,7] = 15 r[5,4] = 26 r[0,3] = 19 r[2,5] = 21 r[2,1] =4 3 r[6,5] = 11 r[1,4] = 25 r[2,6] = 15 r[3,2] = 32 Значения симметричных элементов получить самостоятельно. Задание 2. Решить задачу о коммивояжере. Значения элементов матрицы расстояний: a(1.1) = ∞ a(2.1) = 153 a(3.1) = 32 a(4.1) = 11 a(5.1) = 22 a(1.2) = 25 a(2.2) = ∞ a(3.2) = 72 a(4.2) = 35 a(5.2) = 63 a(1.3) = 15 a(2.3) = 24 a(3.3) = ∞ a(4.3) = 29 a(5.3) = 34 a(1.4) = 13 a(2.4) = 36 a(3.4) = 18 a(4.4) = ∞ a(5.4) = 16 a(1.5) = 46 a(2.5) = 75 a(3.5) = 124 a(4.5) = 38 a(5.5) = ∞ Задание 3. Решить задачу нахождения максимального потока в транспортной сети с помощью алгоритма Форда – Фалкерсона. Исходные данные: Дана сеть S(X,U) x0 – исток сети; x7 – сток сети, где x0 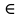 X; x7 X; x7 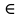 X. X.r[0,1] = 12 r[4,7] = 4 r[6,3] = 13 r[5,7] = 33 r[0,2] = 10 r[4,2] = 18 r[6,7] = 32 r[5,4] = 26 r[0,3] = 19 r[2,5] = 21 r[2,1] = 3 r[6,5] = 11 r[1,4] = 25 r[2,6] = 15 r[3,2] = 32 Задание: 1. Вычислить значение максимального потока на сети S, применяя алгоритм Форда – Фалкерсона. 2. Построить разрез сети S. Задание 4. Выполнить минимизацию булевой функции с помощью карты Карно. f(x,y,z) = 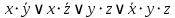 . .По результатам выполнения лабораторной работы оформляется отчет. Задание 1. Решить задачу нахождения кратчайшего маршрута на взвешенном графе с помощью алгоритма Дейкстры. Исходные данные: вершина х0 – начальная; вершина х7 – конечная. r[0,1] = 12 r[4,7] = 4 r[6,3] = 13 r[5,7] = 28 r[0,2] = 10 r[4,2] = 18 r[6,7] = 15 r[5,4] = 26 r[0,3] = 19 r[2,5] = 21 r[2,1] =4 3 r[6,5] = 11 r[1,4] = 25 r[2,6] = 15 r[3,2] = 32 Построим граф 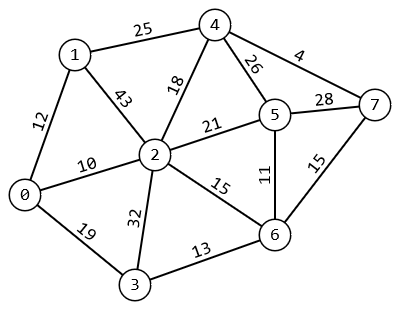 За текущую рассматриваемую вершину с постоянной пометкой возьмем вершину X0 Присвоим L(X0)=0 L(Xi)=∞ 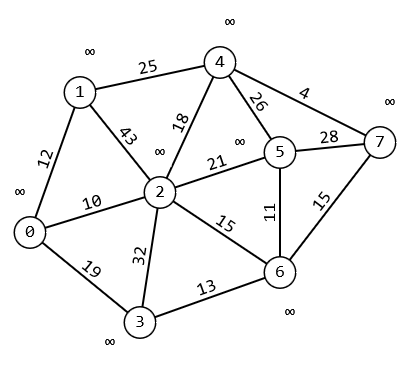 Найдем прямое отображение для текущей рассматриваемой вершины X0 это будут вершины X1, X2 X3. Все вершины, входящие в прямое отображение, имеют временные пометки, поэтому пересчитаем их значение: L(X1)min( ∞ ; 0+12)=12 заменяем метку L(X2)min( ∞; 0+10)=10 заменяем метку L(X3)min( ∞ ; 0+19)= 19 заменяем метку Имеем следующие метки вершин: L(X1)=12 L(X5)= ∞ L(X2)=10 L(X6)= ∞ L(X3)=19 L(X7)= ∞ L(X4)= ∞ Очевидно, что минимальную метку, равную 10, имеет вершина X2. За следующую текущую метку принимаем вершину X2, а метка X0 становится постоянной. 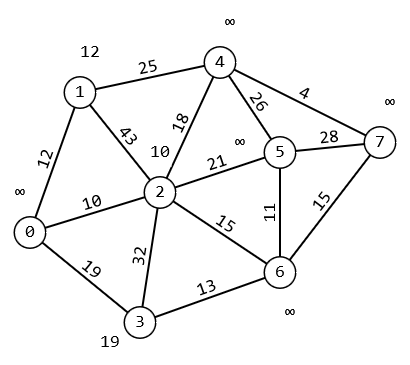 Найдем прямое отображение для текущей рассматриваемой вершины X2 это будут вершины X0, X1, X3, X6, X4, X5. Все вершины, кроме X0, входящие в прямое отображение имеют временные пометки, поэтому пересчитаем их значение: L(X1)min( 12 ; 10+43)=12 оставляем метку L(X3)min( 19 ; 10+32)=19 оставляем метку L(X4)min( ∞ ; 10+18)=28 заменяем метку L(X5)min( ∞; 10+21)=31 заменяем метку L(X6)min( ∞ ; 10+15)= 25 заменяем метку Имеем следующие метки вершин: L(X1) =12 L(X3) = 19 L(X4) =28 L(X6) = 25 L(X5) = 31 L(X7) = ∞ 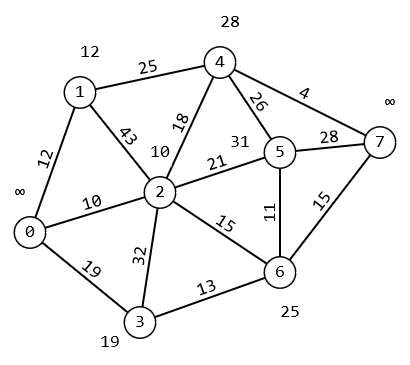 Найдем прямое отображение для текущей рассматриваемой вершины X1, это будут вершины X0, X2, X4. Для X0, X2 метки постоянные. Для X4, временная метка поэтому рассчитаем L(X4)min( 28 ; 12+25)=28 оставляем метку Помечаем X1 как рассмотренную вершину  Перейдем к вершине X4. Найдем прямое отображение для текущей рассматриваемой вершины X1: X2, X5, X7. Для X1, X2 метки постоянные. Для X5, X5 временные метки поэтому рассчитаем L(X5)min( 31 ; 28+26)=31 оставляем метку. L(X7)min( ∞ ; 28+4)=32 заменяем метку. Имеем следующие временные метки L(X3) =19 L(X5) =31 L(X6) =25 L(X7) =32 Помечаем X4 как рассмотренную 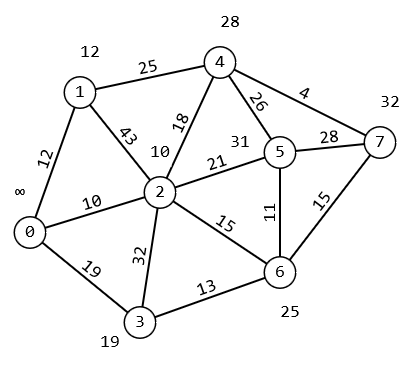 Перейдем к вершине X5 найдем прямое отображение для текущей рассматриваемой вершины X6, это будут вершины X2, X4, X6, X7 для X4, X2 метки постоянные. Для X6, X7 рассчитаем их значения. L(X6)min( 25 ; 31+11)=25 оставляем метку L(X7)min( 32 ; 31+28)=32 оставляем метку Имеем следующие временные метки L(X3) = 19 L(X6) =25 L(X7) =32 Все смежные вершины рассмотрены помечаем вершину X5 как рассмотренную  Перейдем к вершине X3. Найдем прямое отображение для текущей рассматриваемой вершины X3 это буду вершины X0,X2,X6 Для X0,X2 метки постоянные. Для X6 рассчитаем значение. L(X6)min( 25 ; 19+13)=25 оставляем метку L(X6) =25 L(X7) =32 Все смежные вершины рассмотрены помечаем вершину X3 как рассмотренную Перейдем к вершине X6. Найдем прямое отображение для текущей рассматриваемой вершины X6 это будут вершины X2, X3, X5, X7. Для X2, X3, X5 метки постоянные. Для X7 рассчитаем значение. L(X7)min( 32 ; 25+15)=32 оставляем метку Имеем следующие временные метки L(X7) = 32 Все вершины рассмотрены, помечаем оставшуюся вершину: X7, как рассмотренную Все вершины имеют постоянные метки, алгоритм окончен. Для нахождения кратчайшего пути между вершинами X0 и X7. Для построения кротчайшего маршрута пройдем обратный путь от X7 к X0. X7 последовательно используем соотношение L(x*i)+c( x*i, xi)=L( xi), где L( xi) - пометка рассматриваемой вершины , L(x*i) - пометка предшествующей вершины вершине xi, с - вес ребра соединяющий вершины x*i и вершину хi ,). L(X7)=32 L(X5)+c(X5, X7)=31+28 L(X7) L(X6)+c(X6, X7)=25+15 L(X7) L(X4)+c(X4, X7)=28+4= L(X7) Это означает, что в вершину, X7 мы попали из вершины X4. L(X4)=28 L(X1)+c(X1, X4)=12+25=L(X4) L(X2)+c(X2, X4)=10+18 L(X4) В вершину, X4 мы попали из вершины X2, так как 10 минимальное значение. Ответ: кротчайший путь из X0 в X7 имеет длину 32 и проходит по вершинам: X0, X2, X4, X7. Задание 2. Решить задачу о коммивояжере. Исходные данные к задаче нахождения гамильтонова цикла в графе (задача о коммивояжере). Значения элементов матрицы расстояний: a(1.1) = ∞ a(2.1) = 153 a(3.1) = 32 a(4.1) = 11 a(5.1) = 22 a(1.2) = 25 a(2.2) = ∞ a(3.2) = 72 a(4.2) = 35 a(5.2) = 63 a(1.3) = 15 a(2.3) = 24 a(3.3) = ∞ a(4.3) = 29 a(5.3) = 34 a(1.4) = 13 a(2.4) = 36 a(3.4) = 18 a(4.4) = ∞ a(5.4) = 16 a(1.5) = 46 a(2.5) = 75 a(3.5) = 124 a(4.5) = 38 a(5.5) = ∞ Решение: Составим таблицу длин ребер
Для определения нижней границы множества воспользуемся операцией редукции или приведения матрицы по строкам, для чего необходимо в каждой строке матрицы D найти минимальный элемент. di = min(j) dij
Затем вычитаем di из элементов рассматриваемой строки. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.
Такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент: dj = min(i) dij
После вычитания минимальных элементов получаем полностью редуцированную матрицу, где величины di и dj называются константами приведения.
Сумма констант приведения определяет нижнюю границу H: H = ∑di + ∑dj H = 13+24+18+11+16+0+12+0+0+27 = 121 Элементы матрицы dij соответствуют расстоянию от пункта i до пункта j. Поскольку в матрице n городов, то D является матрицей nxn с неотрицательными элементами dij ≥ 0 Каждый допустимый маршрут представляет собой цикл, по которому коммивояжер посещает город только один раз и возвращается в исходный город. Длина маршрута определяется выражением: F(Mk) = ∑dij Причем каждая строка и столбец входят в маршрут только один раз с элементом dij. Шаг №1. Определяем ребро ветвления и разобьем все множество маршрутов относительно этого ребра на два подмножества (i,j) и (i*,j*). С этой целью для всех клеток матрицы с нулевыми элементами заменяем поочередно нули на М(бесконечность) и определяем для них сумму образовавшихся констант приведения, они приведены в скобках.
d(1,2) = 0 + 12 = 12; d(1,4) = 0 + 0 = 0; d(2,3) = 12 + 2 = 14; d(3,4) = 14 + 0 = 14; d(4,1) = 0 + 6 = 6; d(4,5) = 0 + 6 = 6; d(5,4) = 6 + 0 = 6; Наибольшая сумма констант приведения равна (12 + 2) = 14 для ребра (2,3), следовательно, множество разбивается на два подмножества (2,3) и (2*,3*). Исключение ребра (2,3) проводим путем замены элемента d23 = 0 на M, после чего осуществляем очередное приведение матрицы расстояний для образовавшегося подмножества (2*,3*), в результате получим редуцированную матрицу.
Нижняя граница гамильтоновых циклов этого подмножества: H(2*,3*) = 112 + 12 = 124 Нижняя граница гамильтоновых циклов этого подмножества: H(2*,3*) = 121 + 14 = 135 Включение ребра (2,3) проводится путем исключения всех элементов 2-ой строки и 3-го столбца, в которой элемент d32 заменяем на М, для исключения образования негамильтонова цикла. В результате получим другую сокращенную матрицу (4 x 4), которая подлежит операции приведения. После операции приведения сокращенная матрица будет иметь вид:
Сумма констант приведения сокращенной матрицы: ∑di + ∑dj = 0 Нижняя граница подмножества (2,3) равна: H(2,3) = 121 + 0 = 121 ≤ 135 Поскольку нижняя граница этого подмножества (2,3) меньше, чем подмножества (2*,3*), то ребро (2,3) включаем в маршрут с новой границей H = 121 Шаг №2. Определяем ребро ветвления и разобьем все множество маршрутов относительно этого ребра на два подмножества (i,j) и (i*,j*). С этой целью для всех клеток матрицы с нулевыми элементами заменяем поочередно нули на М(бесконечность) и определяем для них сумму образовавшихся констант приведения, они приведены в скобках.
d(1,2) = 0 + 12 = 12; d(1,4) = 0 + 0 = 0; d(3,4) = 14 + 0 = 14; d(4,1) = 0 + 6 = 6; d(4,5) = 0 + 6 = 6; d(5,4) = 6 + 0 = 6; Наибольшая сумма констант приведения равна (14 + 0) = 14 для ребра (3,4), следовательно, множество разбивается на два подмножества (3,4) и (3*,4*). Исключение ребра (3,4) проводим путем замены элемента d34 = 0 на M, после чего осуществляем очередное приведение матрицы расстояний для образовавшегося подмножества (3*,4*), в результате получим редуцированную матрицу.
Нижняя граница гамильтоновых циклов этого подмножества: H(3*,4*) = 121 + 14 = 135 Включение ребра (3,4) проводится путем исключения всех элементов 3-ой строки и 4-го столбца, в которой элемент d43 заменяем на М, для исключения образования негамильтонова цикла. В результате получим другую сокращенную матрицу (3 x 3), которая подлежит операции приведения. После операции приведения сокращенная матрица будет иметь вид:
Сумма констант приведения сокращенной матрицы: ∑di + ∑dj = 6 Нижняя граница подмножества (3,4) равна: H(3,4) = 121 + 6 = 127 ≤ 135 Чтобы исключить подциклы, запретим следующие переходы: (4,2), Поскольку нижняя граница этого подмножества (3,4) меньше, чем подмножества (3*,4*), то ребро (3,4) включаем в маршрут с новой границей H = 127 Шаг №3. Определяем ребро ветвления и разобьем все множество маршрутов относительно этого ребра на два подмножества (i,j) и (i*,j*). С этой целью для всех клеток матрицы с нулевыми элементами заменяем поочередно нули на М(бесконечность) и определяем для них сумму образовавшихся констант приведения, они приведены в скобках.
d(1,2) = 6 + 29 = 35; d(4,1) = 0 + 0 = 0; d(4,5) = 0 + 6 = 6; d(5,1) = 29 + 0 = 29; Наибольшая сумма констант приведения равна (6 + 29) = 35 для ребра (1,2), следовательно, множество разбивается на два подмножества (1,2) и (1*,2*). Исключение ребра (1,2) проводим путем замены элемента d12 = 0 на M, после чего осуществляем очередное приведение матрицы расстояний для образовавшегося подмножества (1*,2*), в результате получим редуцированную матрицу.
Нижняя граница гамильтоновых циклов этого подмножества: H(1*,2*) = 127 + 35 = 162 Включение ребра (1,2) проводится путем исключения всех элементов 1-ой строки и 2-го столбца, в которой элемент d21 заменяем на М, для исключения образования негамильтонова цикла. В результате получим другую сокращенную матрицу (2 x 2), которая подлежит операции приведения. После операции приведения сокращенная матрица будет иметь вид:
Сумма констант приведения сокращенной матрицы: ∑di + ∑dj = 0 Нижняя граница подмножества (1,2) равна: H(1,2) = 127 + 0 = 127 ≤ 162 Поскольку нижняя граница этого подмножества (1,2) меньше, чем подмножества (1*,2*), то ребро (1,2) включаем в маршрут с новой границей H = 127 В соответствии с этой матрицей включаем в гамильтонов маршрут ребра (4,5) и (5,1). В результате по дереву ветвлений гамильтонов цикл образуют ребра: (2,3), (3,4), (4,5), (5,1), (1,2), Длина маршрута равна F(Mk) = 127 1 2 |
