2-Лабораторная_Метрология_2. Лабораторная работа 2 по дисциплине Метрология и радиоизмерения (Учебное пособие Метрология, автор Эрастов В. Е., 1999 г.)
 Скачать 1.42 Mb.
|
|
Министерство образования Российской Федерации Томский межвузовский центр дистанционного образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) ЛАБОРАТОРНАЯ РАБОТА № 2 по дисциплине «Метрология и радиоизмерения» (Учебное пособие «Метрология», автор Эрастов В.Е., 1999 г.) Тема работы: Изучение особенностей использования СИ с различными способами нормирования пределов допускаемой основной погрешности. Выполнил: студент ТМЦДО Содержание 1 Цель работы ………………………..…………………………………3 2 Программа работы ……………………………………………………3 1 Цель работы: Изучение особенностей использования СИ с различными способами нормирования пределов допускаемой основной погрешности. 2 Программа работы 2.1. Расшифруйте условное обозначение класса точности СИ 1.0. Изменяя значение измеряемой ФВ от значения 0,1  до (где предел измерения или конечное значение шкалы), постройте для этого СИ графики следующих зависимостей: абсолютной погрешности  ; относительной погрешности  ; точности СИ  .Анализируя графики, сформулируйте выводы по следующим вопросам: 1) Как изменяется точность СИ этого вида в зависимости от значения измеряемой ФВ? 2) Учитывая, что лабораторные приборы для измерения электрических величин выполняются, как правило, многопредельными, сформулируйте правило, как следует выбирать предел измерения у приборов этого вида, чтобы точность полученных результатов была максимально возможной. Примечание к п. 2.1. Расшифровать условное обозначение класса точности, значит указать: какой вид погрешности для СИ является преобладающим; какая у прибора шкала; что за величина, числовое значение которой указывается на шкале в качестве класса точности; что является нормирующим значением при нормировке предела допускаемой основной погрешности. Ответ. Для класса точности СИ 1.0 преобладает аддитивная составляющая погрешности, шкала прибора линейная. Условное обозначение класса точности представляет собой предел допускаемой основной приведенной погрешности, выраженное в процентах (например, 1,0 %). Нормирующее значение выражено в единицах измеряемой ФВ. Нормирующее значение принимают равным: - конечному значению шкалы прибора  , если нулевая отметка находится на краю или вне шкалы;- сумме конечных значений шкалы прибора (без учета знаков), если нулевая отметка находится внутри шкалы; - номинальному значению измеряемой величины, если таковое установлено. Для приборов со шкалой, градуированной в единицах ФВ, длякоторой принята шкала с условным нулем, нормирующее значение принимается равным разности конечного и начального значения шкалы. Для построения графиков зависимостей условно зададимся пределом измерения =100 (построение выполнялось при помощи программы Mathcad 7,0).Сами графики приведены на рисунках 2.1-2.3. Р 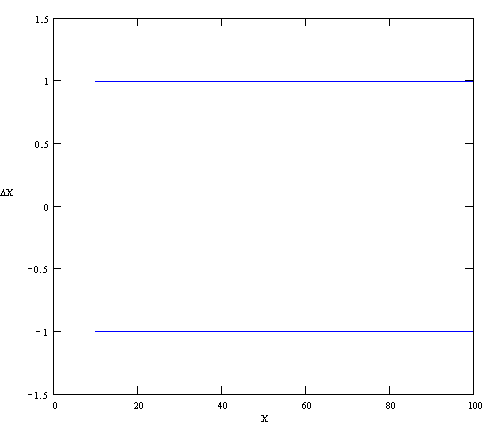 исунок 2.1 График зависимости абсолютной погрешности Р 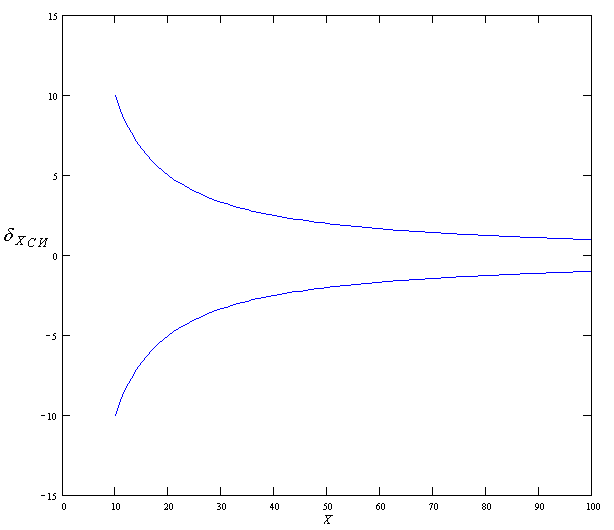 исунок 2.2 График зависимости относительной погрешности Р 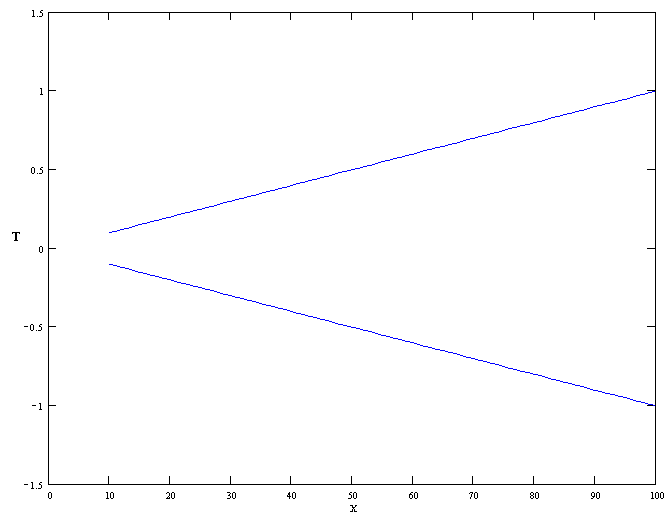 исунок 2.3 График зависимости точности Анализируя графики, можно сделать вывод: 1) точность СИ этого вида увеличивается при увеличении значения измеряемой ФВ. 2) выбирать предел измерения у приборов этого вида следует как можно ближе к измеряемому значению, чтобы точность полученных результатов была максимально возможной.  2.2. Расшифруйте условное обозначение класса точности 1,0 . Выполните все задания п. 2.1 для СИ этого вида. О твет.Для класса точности 1,0 преобладает мультипликативная погрешность. Условное обозначение класса точности представляет предел допускаемой основной относительной погрешности, выраженное в процентах (например, 1,0 %). Г 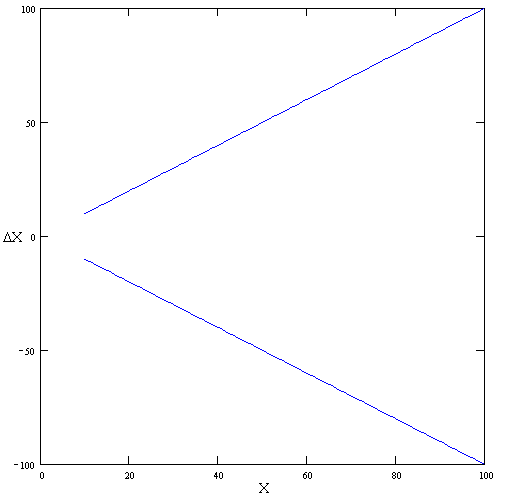 рафики приведены на рисунках 2.4-2.6. Рисунок 2.4 График зависимости абсолютной погрешности Р 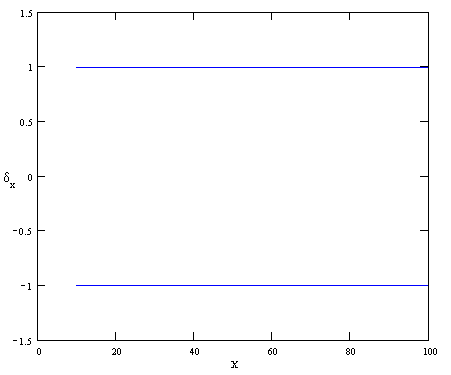 исунок 2.5 График зависимости относительной погрешности 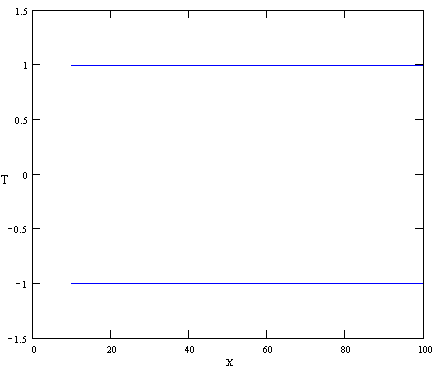 Рисунок 2.6 График зависимости точности Анализируя графики, можно сделать вывод: 1) точность СИ этого вида не изменяется при изменении значения измеряемой ФВ. 2) выбирать предел измерения у приборов этого вида можно практически любой. 2.3. Расшифруйте условное обозначение класса точности  . Выполните все задания п. 2.1 для СИ этого вида.Ответ. Для класса точности СИ 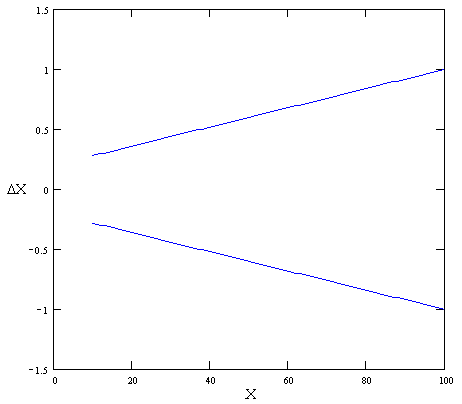имеет место и аддитивная, и мультипликативная составляющая погрешности. Условное обозначение класса точности представляет собой вид дроби, в числителе которой приведенная погрешность в начале шкалы, а в знаменателе - в конце шкалы, выраженные в процентах. Нормирующей величиной является конечное з начение шкалы прибора. Графики приведены на рисунках 2.7-2.9. Рисунок 2.7 График зависимости абсолютной погрешности Р 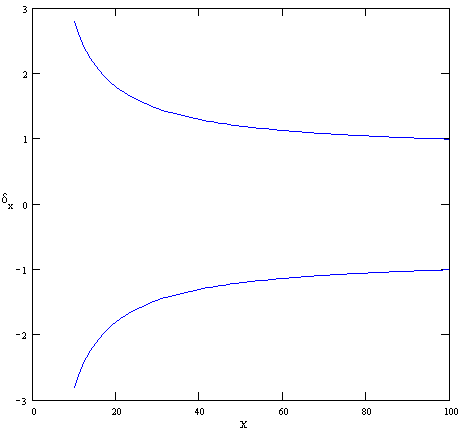 исунок 2.8 График зависимости относительной погрешности Р 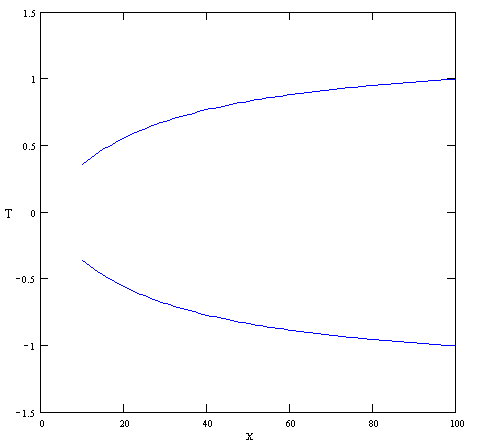 исунок 2.9 График зависимости точности Анализируя графики, можно сделать вывод: 1) точность СИ этого вида увеличивается при увеличении значения измеряемой ФВ. 2) выбирать предел измерения у приборов этого вида следует как можно ближе к измеряемому значению, чтобы точность полученных результатов была максимально возможной. 2  .4. Расшифруйте условное обозначение класса точности 1,0.Ответ. Д ля класса точности СИ 1.0 преобладает аддитивная составляющая погрешности, шкала прибора имеет резко нелинейную шкалу. Условное обозначение класса точности представляет собой предел допускаемой основной приведенной погрешности, выраженное в процентах (например, 1,0 %). Нормирующее значение принято равным длине шкалыДля того чтобы выяснить все особенности использования СИ этого вида, необходимо рассмотреть конкретное СИ. Наиболее характерным прибором, относящимся к СИ этого вида, является омметр. Омметры непосредственной оценки строятся на базе микроамперметров магнитоэлектрической системы по последовательной и параллельной схемам (см. рис. 2.10 и рис. 2.11). Для любой из схем величина измеренного сопротивления  подключается к входным зажимам омметра и преобразуется измерительнойцепью прибора в изменение тока, протекающего через измерительный прибор (микроамперметр). Связь между величиной сопротивления 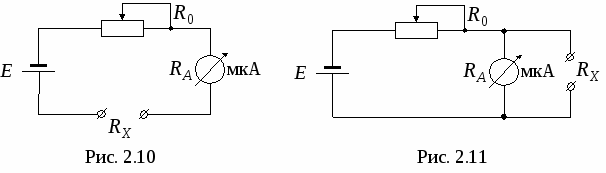 и величиной тока, протекающего через микроамперметр однозначная, то есть шкала микроамперметра может быть отградуирована в значениях измеряемого сопротивления. Причем переградуировать шкалу микроамперметра можно расчетным путем. Пусть омметры строятся на базе микроамперметра с пределом измерения  мкА, класса 1.0, имеющего шкалу прямолинейной формы со световым указателем, число делений шкалы  , а геометрическая длина ее  мм.Для микроамперметра класса 1,0 с мкА абсолютная погрешность, как следует из п. 2.1, в любой точке шкалы постоянна и равна: кл. точн. (мкА) или 1 дел. шкалы (т. к. шкала равномерная и ), или 1 мм шкалы (т. к. шкала имеет мм и разделена на 100 одинаковых делений).Следовательно, в рассматриваемом случае можно говорить, что абсолютная погрешность прибора равна 1 мм шкалы в любой точке (помня о том, что вся шкала имеет длину 100 мм и отклонение указателя на всю шкалу соответствует току в 100 мкА). 2.4.1. Для омметра по последовательной схеме (см. рис. 2.10) переградуируйте шкалу микроамперметра расчетным путем, если известно, что  В, внутреннее сопротивление источника  ,  Ом, а  выбирается из тех условий, что при  (входные зажимы омметра закорочены) ток через микроамперметр должен соответствовать мкА.Обратите внимание на то, что нулевая отметка шкалы у такого омметра находится справа (на отметке, соответствующей току через прибор в 100 мкА). Для того, чтобы переградуировать шкалу расчетным путем, проделайте следующее: 1) Получите в общем виде уравнение шкалы омметра n[дел.]  , где n деления шкалы микроамперметра.Ответ. Приняв длину шкалы за 100 мм и сопоставив ее с током, протекающим через микроамперметр, можно получить уравнение шкалы по закону Ома: n=  ,где U – напряжение источника питания, Rобщ=R0+RA+RX – общее сопротивление всей цепи. R0 можно найти закоротив RX :  Ом.2) Оцените диапазон значений измеряемого сопротивления для данной схемы омметра, для чего воспользовавшись уравнением шкалы, полученным в п.1, определите величину для отклонения указателя на одно деление и на 99 делений шкалы микроамперметра.Ответ. Воспользовавшись уравнением шкалы, получим формулу для расчета RX:  .Тогда, для отклонения указателя на одно деление:  Ом, или 2,97 МОм.Для отклонения указателя на 99 делений шкалы микроамперметра:  Ом.3) Составьте градуировочную таблицу, выбрав в диапазоне измеряемых значений ряд точек, охватывающих всю шкалу (удобных, на ваш взгляд, для получения рабочей шкалы омметра) и рассчитав по уравнению шкалы количество делений, на которое отклонится световой указатель микроамперметра при измерении соответствующего сопротивления.Ответ. Таблица 2.1 Данные для градуировки шкалы омметра.
4) В масштабе 1:1 изобразите шкалу омметра в таком виде: 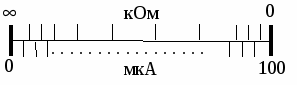 Для полученного омметра абсолютная погрешность в любой точке шкалы остается также постоянной и равной 1 мм шкалы, то есть погрешность аддитивная. Класс точности таким приборам присваивается по величине приведенной погрешности, выраженной в процентах. Что же следует использовать в качестве нормирующей величины, если у омметра нет определенного конечного значения измеряемой величины (  не может быть нормирующей величиной), а абсолютную погрешность удобно выражать в долях длины шкалы?Очевидно, в качестве нормирующей величины следует выбрать геометрическую длину шкалы в мм. Следовательно, для полученного вами омметра  и 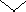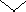класс точности его 1,0 . Символ внизу числового значения класса точности указывает на то, что шкала у приборарезко нелинейная и нормировка предела допускаемой основной погрешности ведется относительно геометрической длины шкалы.Ответ. 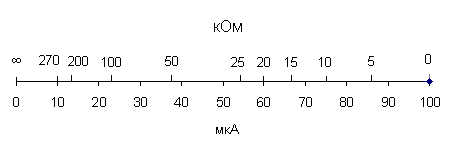 Рисунок 2.12 Шкала омметра 5) Выбрав ряд характерных точек на шкале омметра (не менее 10 в пределах всей шкалы), подсчитайте для каждой точкирасчетные значения абсолютной и относительной погрешностей и точности прибора и постройте графики:  ;  ;  .Для определения абсолютной погрешности в единицах измеряемой величины (в омах) в некоторой точке шкалы, соответствующей измеряемому сопротивлению  , необходимо по градуировочной таблице (или по построенной шкале омметра) найти число делений  , соответствующих этому сопротивлению, затем рассчитать (используя уравнение шкалы) величину сопротивления для точки  (что соответствует верхней границе интервала неопределенности для , т. е.  ) и для точки  (что соответствует нижней границе интервала неопределенности для , т. е.  ). В большинстве случаев  , т. е. границы интервала неопределенности для измеряемого сопротивления в единицах измеряемой величины получаются несимметричными (влияние резкой нелинейности шкалы). Для построения графиков используйте большее по модулю значение погрешности.Сравните полученные графики с графиками, полученными в п. 2.1 для СИ, у которого также преобладает аддитивная погрешность, но шкала прибора линейная. Ответ. Данные расчетов для выбранных точек сведены в таблицу 2.2, а графики приведены на рисунках 2.13 - 2.15 соответственно. Таблица 2.2 Данные расчета погрешности и точности
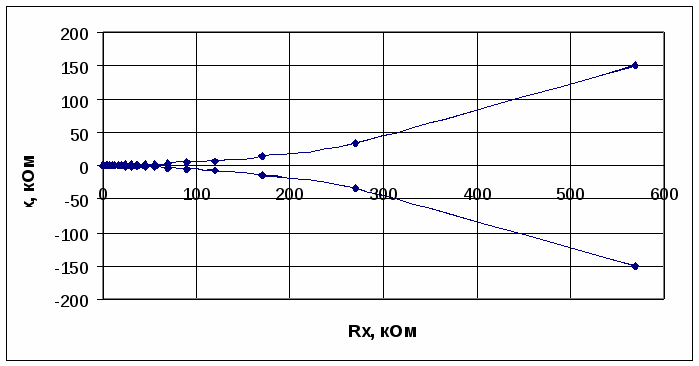 Рисунок 2.13 График зависимости абсолютной погрешности 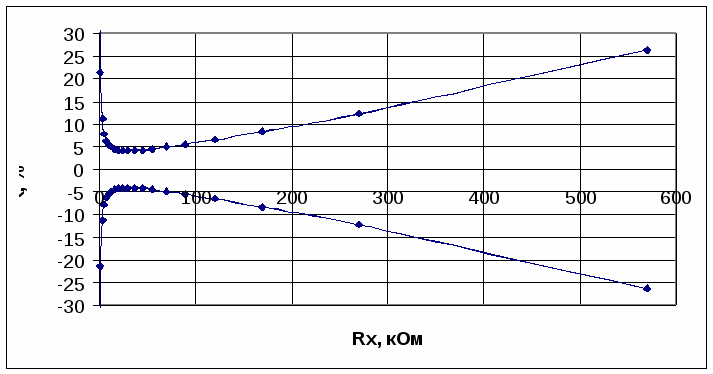 Р 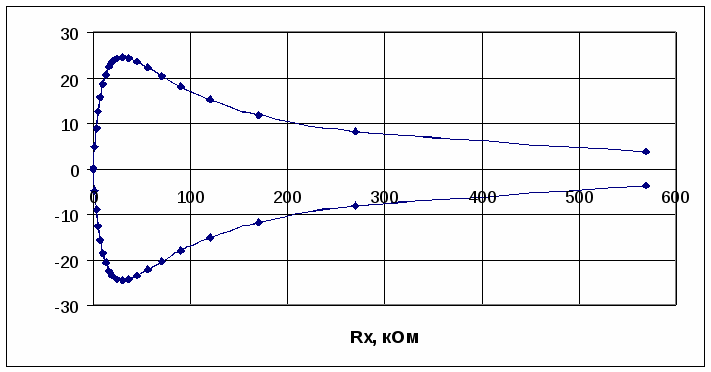 исунок 2.14 График зависимости относительной погрешности Рисунок 2.15 График зависимости точности Сравнивая эти графики с графиками, полученными в п. 2.1 для СИ, у которого также преобладает аддитивная погрешность, но шкала прибора линейная можно отметить: 1) абсолютная погрешность в первом случае не меняется с изменением измеряемой величины, во втором же случае с увеличением сопротивления абсолютная погрешность также увеличивается, 2) относительная погрешность в первом случае уменьшается с увеличением измеряемой величины, во втором же случае с увеличением сопротивления относительная погрешность в начале диапазона резко уменьшается до определенного значения, затем происходит ее увеличение, 3) точность, как обратная функция от относительной погрешности, ведет себя соответственно. 2.4.2. Для омметра по параллельной схеме (см. рис. 2.11) переградуируйте шкалу микроамперметра расчетным путем при тех же условиях, что и в п. 2.4.1. Ответ. Приняв длину шкалы за 100 мм и сопоставив ее с током, протекающим через микроамперметр, можно получить уравнение шкалы по закону Ома: n= 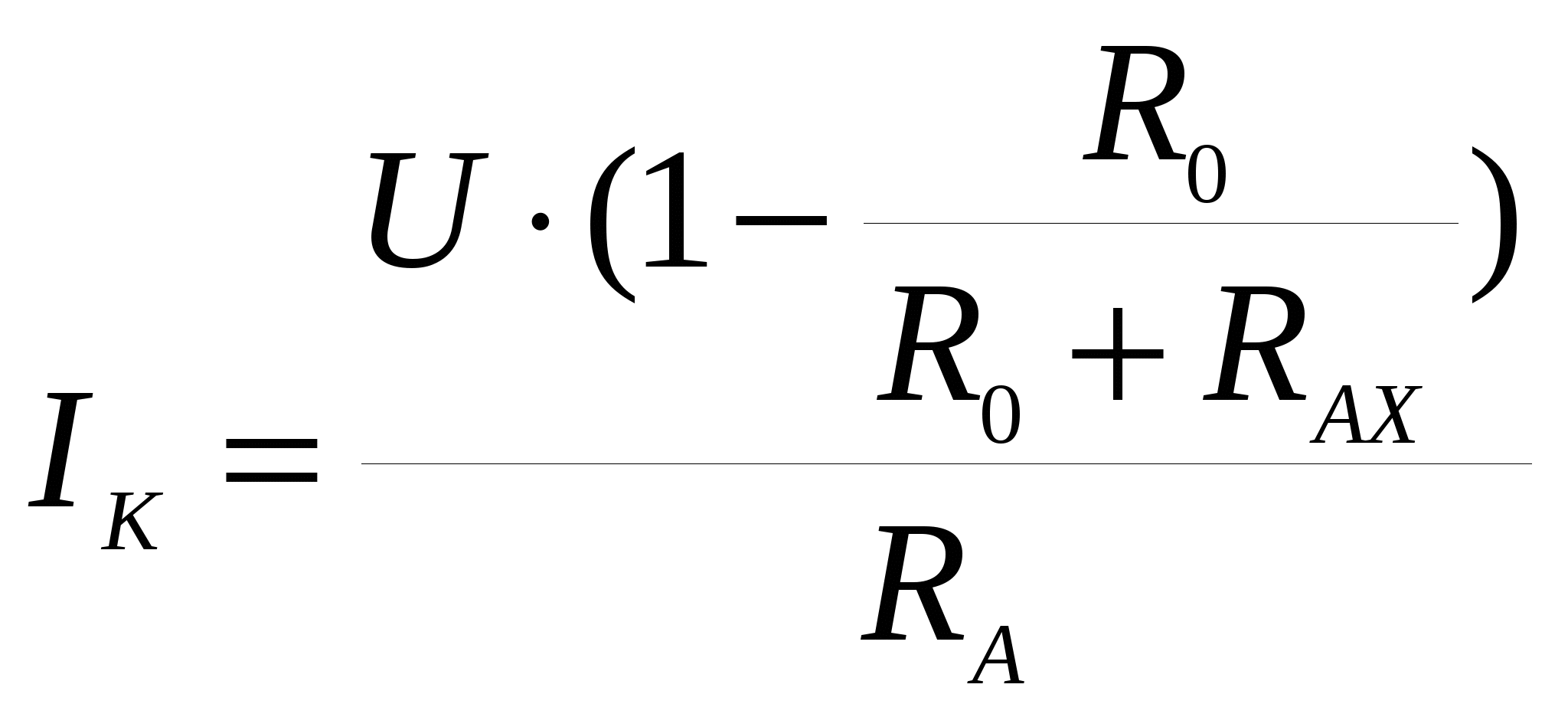 ,где U – напряжение источника питания,  –сопротивление параллельного соединения амперметра и измеряемого сопротивления. R0 можно найти оборвав RX : Ом или 29 кОм.Таблица 2.3 Данные для градуировки шкалы омметра.
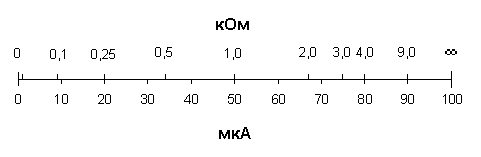 Рисунок 2.16 Шкала омметра Данные расчетов сведены в таблицу 2.4, а графики приведены на рисунках 2.17 - 2.19 соответственно. Таблица 2.4 Данные расчета погрешности и точности
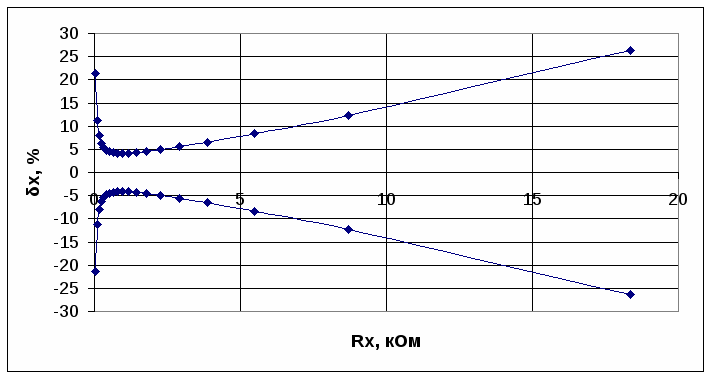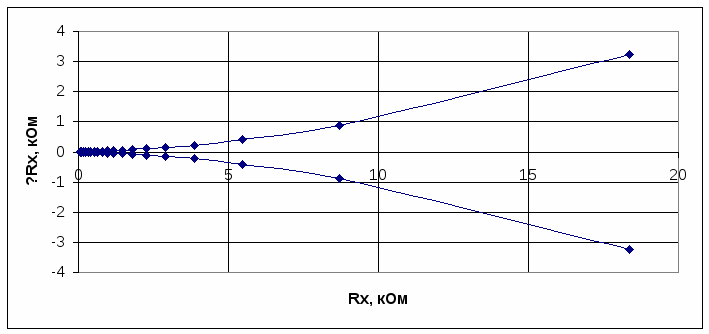  Рисунок 2.17 График зависимости абсолютной погрешности Рисунок 2.18 График зависимости относительной погрешности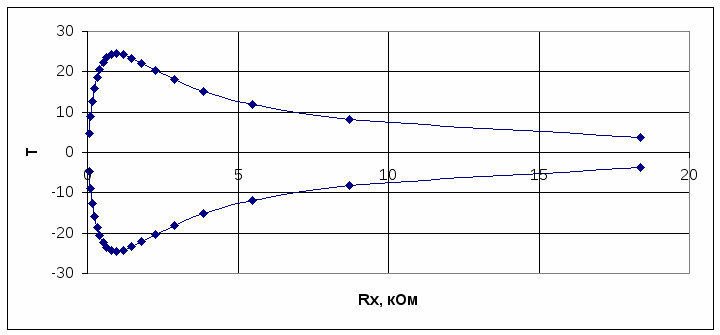 Рисунок 2.19 График зависимости точности Сравнив результаты, полученные в п.п. 2.4.1 и 2.4.2, можно отметить, что: 1) характер зависимостей погрешностей и точности для омметра по параллельной схеме совпадает с теми зависимостями, которые получены для последовательной схемы омметра в п. 2.4.1. 2) разница между омметрами, построенными по последовательной и параллельной схемам состоит в том, что ток через амперметр в последовательной схеме с увеличением измеряемого сопротивления уменьшается. Шкала градуирована в Ом от до 0. При параллельной схеме ток увеличивается при увеличении сопротивления. Шкала градуирована в Ом от 0 до . 3) последовательная схема омметра применяется для измерения больших сопротивлений (до 106 – 107 Ом), параллельная схема применяется для измерения небольших сопротивлений (до 103 Ом). 2 .4.3. Опишите порядок действий при определении абсолютной погрешности результата измерения в единицах измеряемой величины (в Ом) любым из двух омметров при реальном использовании прибора, когда уравнение шкалы неизвестно, а имеется только шкала реального омметра и известны: отсчет по шкале для измеряемого сопротивления; класс точности омметра и длина его шкалы. Приведите конкретный пример с использованием одной из полученных вами шкал, задав отсчет по шкале для самостоятельно и считая, что класс точности омметра 2.0, а геометрическая длина шкалы та же 100 мм.Ответ. Д ля класса точности СИ 2.0 преобладает аддитивная составляющая погрешности, шкала прибора имеет резко нелинейную шкалу. Условное обозначение класса точности представляет собой предел допускаемой основной приведенной погрешности, выраженное в процентах (2,0 %). Нормирующее значение принято равным длине шкалы.Возьмем для примера омметр, построенный по последовательной схеме, и определим абсолютную погрешность результата измерения в единицах измеряемой величины (в Ом), задав величину измеряемого сопротивления равной 20 кОм. По известной формуле  ,где  - абсолютную погрешность результата измерения в единицах шкалы; - класс точности омметра (предел допускаемой погрешности); L – длина шкалы, определим абсолютную погрешность результата измерения в единицах шкалы  мм .Теперь, по имеющейся шкале найдем абсолютную погрешность результата измерения для 20 кОм:  1,7 кОм.Увеличенный участок шкалы приведен на рисунке 2.20. 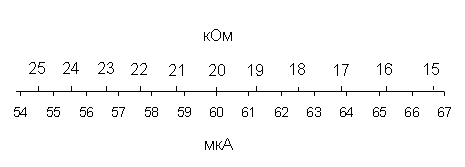 Рисунок 2.20 Увеличенный участок шкалы |