лаба2. Лабораторная работа 2 по дисциплине Нейронечёткие нейронные сети Выполнил студент группы бис21 Альбаили К. С
 Скачать 50.36 Kb. Скачать 50.36 Kb.
|
|
Министерство образования и науки Российской Федерации ФГБОУ ВО «ТГТУ» Институт автоматики и информационных технологий кафедра «Информационные системы и защита информации» Лабораторная работа №2 по дисциплине: «Нейронечёткие нейронные сети» Выполнил: студент группы БИС-21 Альбаили К.С. Проверил: Нурутдинов Г.Н. Тамбов 2019 г. Цель: в пакете MATLAB создать и использовать нейронную сеть для прогнозирования значений процесса. Постановка задачи: имеется сигнал (функция времени), описываемый соотношением x(t)=2*cos(pi*t), который подвергается дискретизации с интервалом 0,025 с. Построим линейную НС, позволяющую прогнозировать будущее значение подобного сигнала по 6 предыдущим . Основная часть. Зададим диапазон времени от 0 до 5 секунд. >> t=0:0.025:5; >> x=2*cos(pi*t); Определяем длину диапазона. >> Q=length(x); Создадим нулевую матрицу P, размером 5 на Q. >> P= zeros(5,Q); >> P(1,2:Q) = x(1,1:(Q-1)); >> P(2,3:Q) = x(1,1:(Q-2)); >> P(3,4:Q) = x(1,1:(Q-3)); >> P(4,5:Q) = x(1,1:(Q-4)); >> P(5,6:Q) = x(1,1:(Q-5)); Создание новой НС с именем s >> s = newlind(P,x); Расчет прогнозируемых значений >> y = sim(s,P); Создание графиков исходного сигнала прогноза >> plot(t,y,t,x,'*') >> xlabel('Время'); >> ylabel('Прогноз - Сигнал +'); >> title ('Выход сети и действительные значения'); 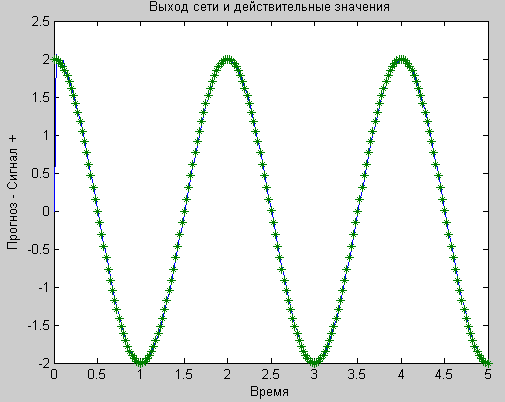 Рисунок 1 – График на основе прогнозируемых значений Расчет и создание графика ошибки прогноза >> e = x-y; >> plot (t,e) >> hold on >> plot([min(t) max(t)], [0 0], ':r') >> hold off >> xlabel('Время'); >> ylabel('Ошибка'); >> title('Сигнал ошибки'); 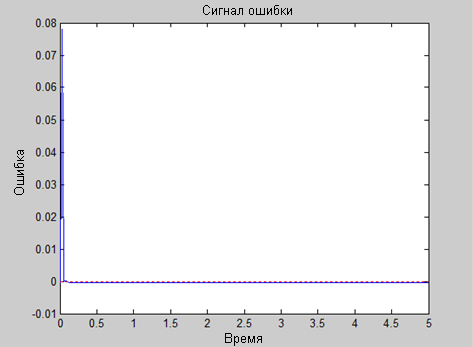 Рисунок 2 – График ошибок Вывод: в данной лабораторной работе, я научился создавать и использовать нейронную сеть для прогнозирования значений процесса, с помощью встроенного пакета нейронных сетей MATLAB. На основе полученных данных с нейронной сети, построили график прогнозируемых значений в соответствии с заданными интервалами. Так же научился строить график ошибок на основании которого, можно сделать вывод, что нейронная сеть максимально точно прогнозирует значения. |
