2 лр. Лабораторная работа 2 по дисциплине Организация эвм и вс по теме Оценка производительности процессора Группа абс023 Студенты Кисель А. В
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Лабораторная работа №2 по дисциплине «Организация ЭВМ и ВС» по теме «Оценка производительности процессора» Группа: АБс-023 Студенты: Кисель А. В. Преподаватель: Перышкова Е.Н. НОВОСИБИРСК 2022 Цель работы: Реализовать программу для оценки производительности процессора (benchmark). Задачи: 1. Написать программу(ы) (benchmark) на языке С/С++/C# для оценки производительности процессора. В качестве набора типовых задач использовать либо минимум 3 функции выполняющих математические вычисления, либо одну функцию по работе с матрицами и векторами данных с несколькими типами данных. Обеспечить возможность в качестве аргумента при вызове программы указать общее число испытаний для каждой типовой задачи (минимум 10). Входные данные для типовой задачи сгенерировать случайным образом. 2. С помощью системного таймера (библиотека time.h, функции clock() или gettimeofday()) или с помощью процессорного регистра счетчика TSC реализовать оценку в секундах среднего времени испытания каждой типовой задачи. Оценить точность и погрешность (абсолютную и относительную) измерения времени (рассчитать дисперсию и среднеквадратическое отклонение). 3. Результаты испытаний в самой программе (или с помощью скрипта) сохранить в файл в формате CSV со следующей структурой: [PModel;Task;OpType;Opt;InsCount;Timer;Time;LNum;AvTime;AbsErr;RelErr;TaskPerf], где PModel – Processor Model, модель процессора, на котором проводятся испытания; Task – название выбранной типовой задачи (например, sin, log, saxpy, dgemv, sgemm и др.); OpType – Operand Type, тип операндов, используемых при вычислениях типовой задачи; Opt – Optimisations, используемы ключи оптимизации (None, O1, O2 и др.); InsCount – Instruction Count, оценка числа инструкций при выполнении типовой задачи; Timer – название функции обращения к таймеру (для измерения времени); Time – время выполнения отдельного испытания; LNum – Launch Numer, номер испытания типовой задачи. AvTime –Average Time, среднее время выполнения типовой задачи из всех испытаний[секунды]; AbsError – Absolute Error, абсолютная погрешность измерения времени в секундах; RelError – Relative Error, относительная погрешность измерения времени в %; TaskPerf – Task Performance, производительность (быстродействие) процессора при выполнении типовой задачи. 3. * Оценить среднее время испытания каждой типовой задачи с разным типом входных данных (целочисленные, с одинарной и двойной точностью). 3. ** Оценить среднее время испытания каждой типовой задачи с оптимизирующими преобразования исходного кода компилятором (ключи –O1, O2, O3 и др.). 3. *** Оценить и постараться минимизировать накладные расходы (время на вызов функций, влияние загрузки системы и т.п.) при испытании, то есть добиться максимальной точности измерений. 4. Построить сводную диаграмму производительности в зависимости от задач и выбранных исходных параметров испытаний. Оценить среднее быстродействие (производительность) для равновероятного использования типовых задач. Ход работы Работа выполнена на виртуальном компьютере под управлением операционной системы Linux Debian 10 на языке программирования С++. Создаём файл с расширением .cpp с исходным кодом представленном в приложении. Далее компилируем программу при помощи команды g++ –o Source –O0 Source.cpp и запускаем программу ./Source (рисунок 1). 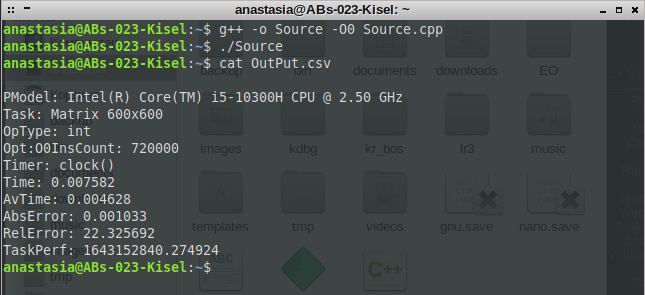 Рис. 1 – Компилирование программы и запуск программы При помощи команды cat просмотрим содержимое файла OutPut.csv (рисунок 2).  Рис. 2 – Результат работы программы для исходных данных типа int без оптимизации Результат работы программы для исходных данных типа int с ключом оптимизации О1 (рисунок 3). 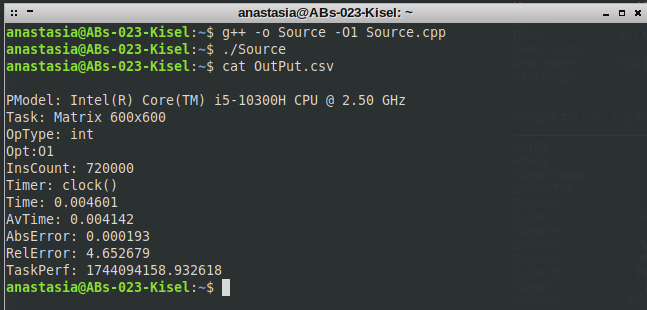 Рис. 3 – Результат работы программы для исходных данных типа int с ключом оптимизации О1 Результат работы программы для исходных данных типа int с ключом оптимизации О2 (рисунок 4). 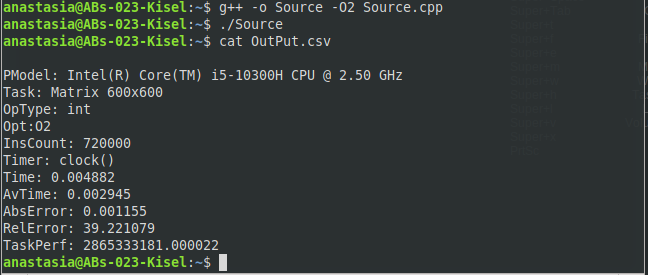 Рис. 4 – Результат работы программы для исходных данных типа int с ключом оптимизации О2 Результат работы программы для исходных данных типа int с ключом оптимизации О3 (рисунок 5 – 6). 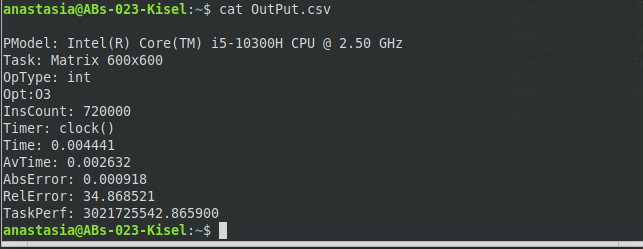 Рис. 5 – 6 – Результат работы программы для исходных данных типа int с ключом оптимизации О3 Результат работы программы для исходных данных типа float без оптимизации (рисунок 7). 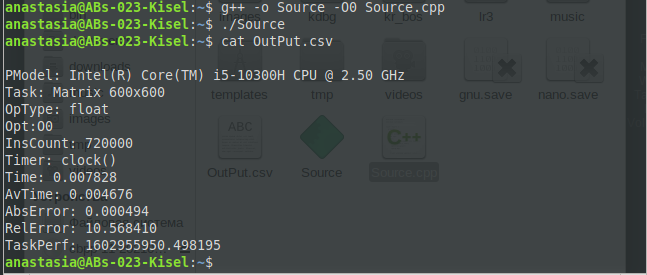 Рис. 7 – Результат работы программы для исходных данных типа float без оптимизации Результат работы программы для исходных данных типа float с ключом оптимизации О1 (рисунок 8). 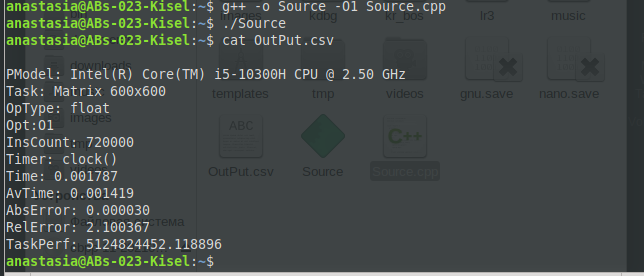 Рис. 8 – Результат работы программы для исходных данных типа float с ключом оптимизации О1 Результат работы программы для исходных данных типа float с ключом оптимизации О2 (рисунок 9). 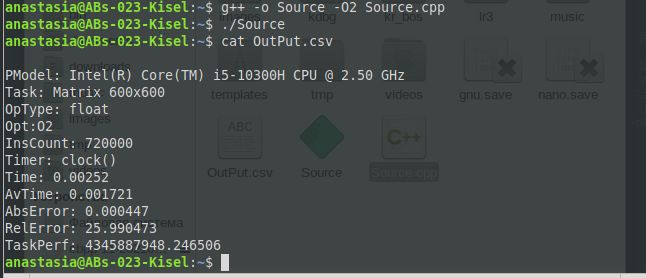 Рис. 9 – Результат работы программы для исходных данных типа float с ключом оптимизации О2 Результат работы программы для исходных данных типа float с ключом оптимизации О3 (рисунок 10). 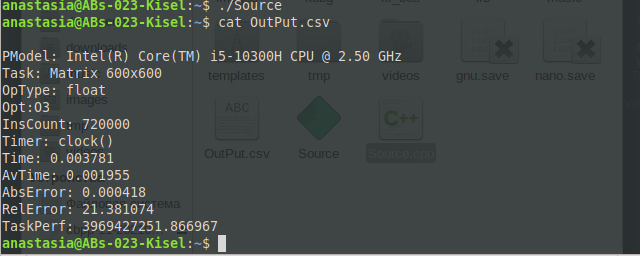 Рис. 10 – Результат работы программы для исходных данных типа float с ключом оптимизации О3 Результат работы программы для исходных данных типа double без оптимизации (рисунок 11) 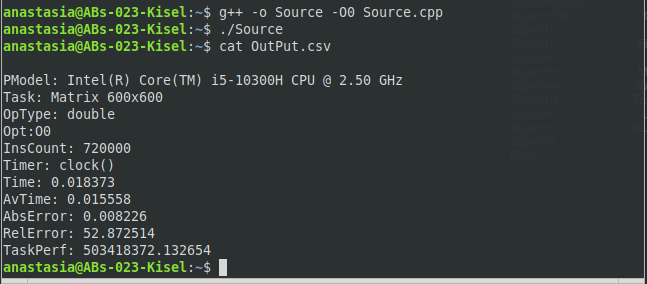 Рис. 11 – Результат работы программы для исходных данных типа double без оптимизации . Результат работы программы для исходных данных типа double с ключом оптимизации О1 (рисунок 12) 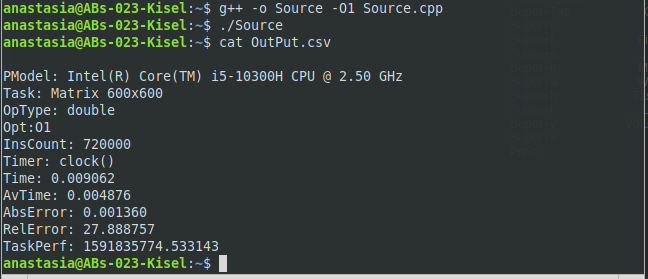 Рис. 12 – Результат работы программы для исходных данных типа double с ключом оптимизации О1 Результат работы программы для исходных данных типа double с ключом оптимизации О2 (рисунок 13). 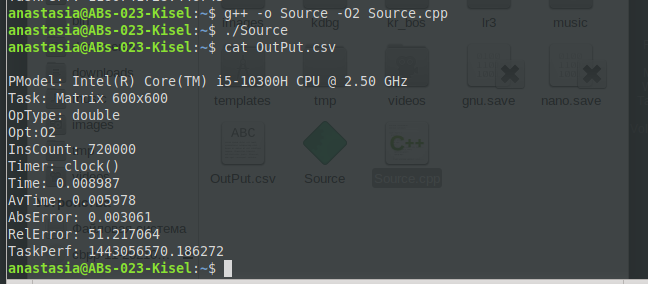 Рис. 13 – Результат работы программы для исходных данных типа double с ключом оптимизации О2 Результат работы программы для исходных данных типа double с ключом оптимизации О3 (рисунок 14) 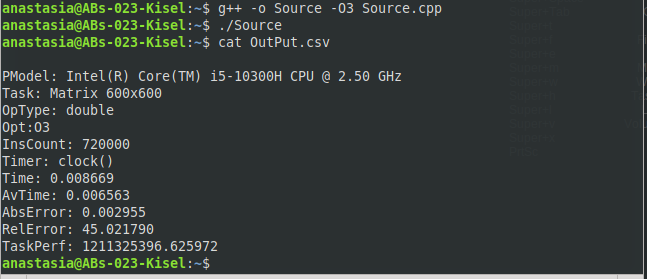 Рис. 14 – Результат работы программы для исходных данных типа double с ключом оптимизации О3 Сводная диаграмма производительности в зависимости выбранных исходных параметров испытаний и ключей оптимизации (рисунок 15). 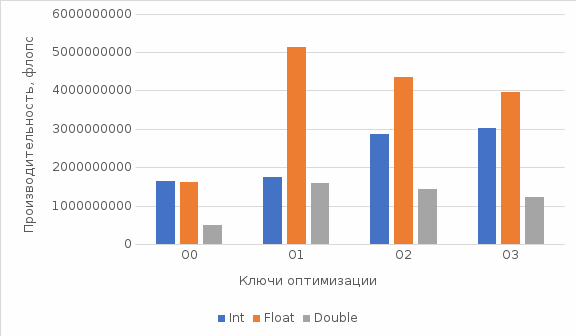 Рис. 15 – Зависимость производительности процессора от исходных данных и ключей оптимизации Вывод: В ходе выполнения лабораторной работы была произведена оценка производительности процессора. Для оценки производительности использовалась задача на заполнение массива и прибавление к каждому элементу единицы. Результаты испытаний показали, что при исходных данных типа Float производительность самая высокая, а при исходных данных типа Double – самая низкая. На измерения производительности могут повлиять разные факторы, как сама программа, так и внешние факторы, при которых они постоянно меняется. Приблизительную производительность процессора с разными типами данных мы можем увидеть на графике. Также результаты зависели от типа оптимизации исходного кода. Так, например, по графику можно заметить, что производительность процессора была самой минимальной, когда оптимизация кода не использовалась. Из результатов также можно заметить, что оптимизация кода с ключом О3 для типов float и double оказалась менее эффективна, чем оптимизация кода с ключом О2, т.к. оптимизация с ключом О3 использует агрессивные методы, которые замедляют работу приложения. Приложение: #include #include #include #include #include #include #include |
