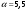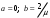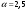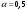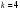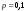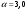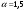Применение уравнений Поллачека-Хинчина. Лабораторная работа 2 Применение формулы Полячека Хинчина Вариант 14 Содержание Задание 3 Выполнение работы 4

• Название: Лабораторная работа 2 Применение формулы Полячека Хинчина Вариант 14 Содержание Задание 3 Выполнение работы 4
• Анкор: Применение уравнений Поллачека-Хинчина
• Дата: 18.08.2022
• Размер: 0.81 Mb.
• Имя файла: Lab2.docx
• Тип: Лабораторная работа; #648045

Лабораторная работа №2

Применение формулы Полячека – Хинчина

Вариант 14

Содержание

1.Задание 3

2.Выполнение работы 4

2.1 Расчёт нормированной дисперсии для каждой СМО 4

2.2 Функции для расчёта вероятностно-временных характеристик СМО. 5

2.3 Скриншоты вызова функций с подставленными значениями аргументов. 6

2.3 Графики зависимостей вероятно-временных характеристик СМО от входной нагрузки 10

2.4 Выводы по проделанной работе 11

3.Список литературы 11

1. Задание

В данной лабораторной работе предполагается сравнить вероятностно-временные характеристики систем массового обслуживания типа M/M/1, M/D/1, полученные с помощью формул Полячека-Хинчинас характеристиками СМО, заданного по варианту типа (табл. 2).

Используя данные из табл. 2, задать параметры исследуемых систем массового обслуживания. Вычислить значения нормированной дисперсии исследуемых СМО . Для вычисления математического ожидания и дисперсии воспользоваться любым справочником по теории вероятностей и математической статистике, например, [5] (или см. ПРИЛОЖЕНИЕ 1).

Получить искомые характеристики:

• 
  среднее количество заявок в СМО ;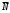
  
• 
  среднее количество заявок в очереди СМО ;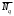
  
• 
  среднее время пребывания заявки в СМО ;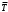
  
• 
  среднее время ожидания заявкой обслуживания .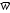
  

Примечание 5: При этом диапазон изменения интенсивности входящего в СМО потока заявок  задать, начиная с 0, и таким образом, чтобы сохранить эргодичность системы .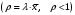

Построить семейство зависимостей описанных выше характеристик от входной нагрузки для различных СМО.

Объяснить полученные результаты.

Индивидуальное задание.

Вариант 14.

Таблица 2. Варианты заданий

µ, с-1		5	1	15	4.5	8
Дополнительные параметры распределения	Распределение времени обслуживания
	Гамма	16	38	12	8	32
	Равномерное	22	3	31	34	6
	Логнормальное	44	49	40	2	18
	Вейбулла	35	17	50	21	41
	Эрланга	9	29	23	46	15
	Гиперэкспоненциальное 2-го порядка	13	7	1	11	27
–	Рэлея	28	33	26	19	43
–	Максвелла	4	47	37	5	36
	Парето	24	45	14	25	10
	Обратное гауссовское	39	20	42	30	48

μ=15 – интенсивность входного потока

Обслуживание- распределение Парето, α=3.0;

2. Выполнение работы

Используем формулу Поллачека-Хинчина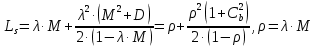

<1

Где Ls- среднее число клиентов в системе

В этой формуле 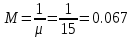c- среднее время обработки заявки, одинаково для обеих СМО, D- дисперсия времени обработки, различаетсядля двух типов СМО, 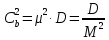- нормированная дисперсия

2.1 Расчёт нормированной дисперсии для каждой СМО

1) M/M/1

Экспоненциальный закон обслуживания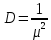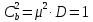





2) M/D/1

Постоянное время обслуживания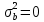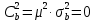





3) M/G/1

Время обслуживания распределено по закону Парето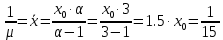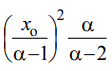





Отсюда .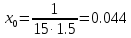

Дисперс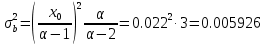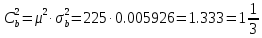ия

- нормированная дисперсия

2.2 Функции для расчёта вероятностно-временных характеристик СМО.

Общие формулы стационарных СМО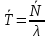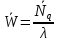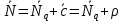







Поэтому получаем расчетные формулы для характеристик СМО:\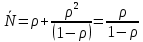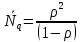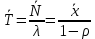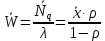

1. 
   M/M/1
   

2. 
   M/D/1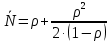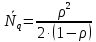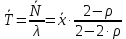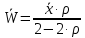
   

3. 
   M/G/1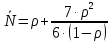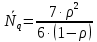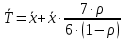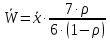
   

2.3 Скриншоты вызова функций с подставленными значениями аргументов.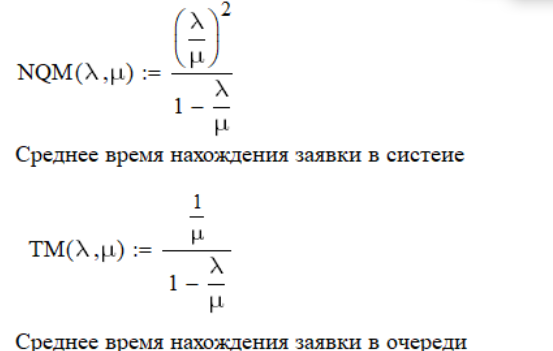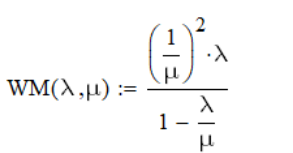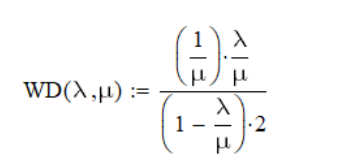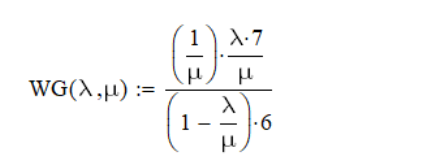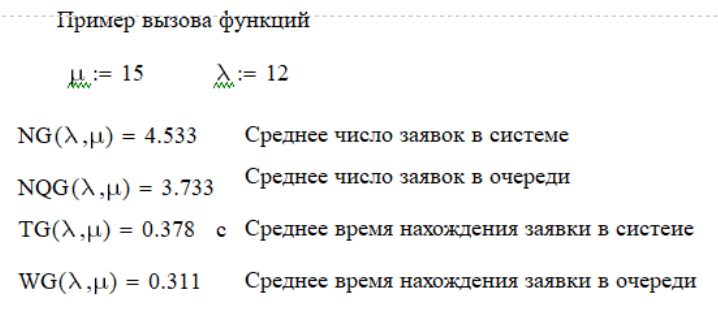

2.3 Графики зависимостей вероятно-временных характеристик СМО от входной нагрузки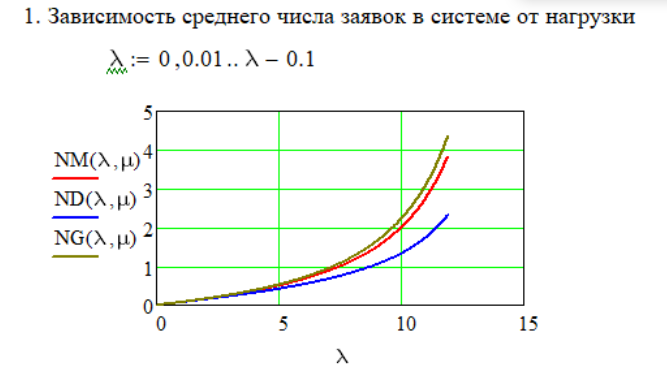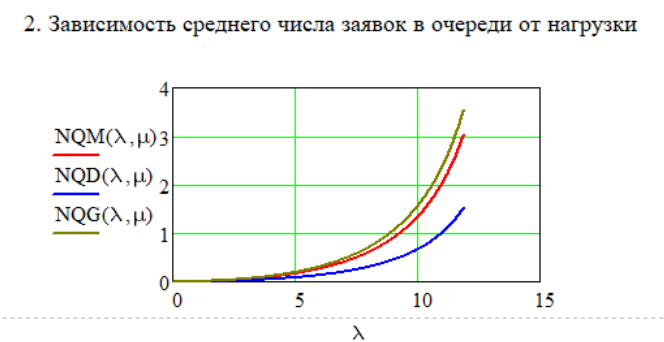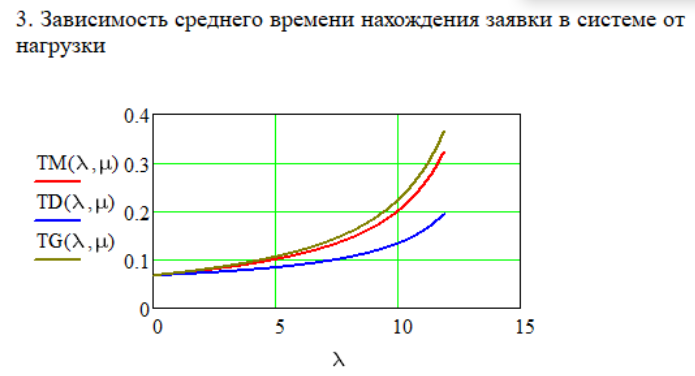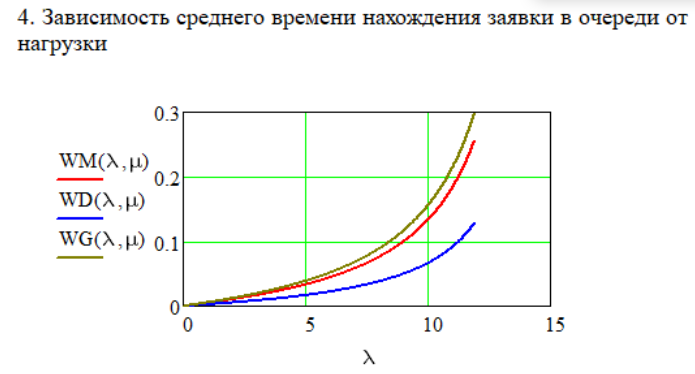

4. Выводы по проделанной работе

На основе формулы Полачека-Хинчина произведен сравнительный анализ временно-вероятностных характеристик СМО типа М/D/1, M/M/1, M/G/1 с распределением Парето времени обслуживания заявки . Все данные СМО характеризуются одинаковой средней производительностью μ, но различной дисперсией времени обработки, та что 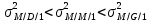. В ходе выполнения лабораторной работы были построены графики характеристик СМО в зависимости от нагрузки и установлено, что для СМО с большей дисперсией времени обработки соответственно больше такие характеристики как средний размер очереди и время ожидания обслуживания.

3. Список литературы

1. 
   Клейнрок Л. Теория массового обслуживания. – М.: Машиностроение, 1979. – 432 с.
   
2. 
   Башарин, Г.П. Лекции по математической теории телетрафика [Электронный ресурс] : учебное пособие / М. : Российский университет дружбы народов, 2009. — 146 c.— Режим доступа:http://www.iprbookshop.ru/11564.htmlпо паролю.
   
3. 
   Вентцель Е.С. Теория вероятностей : учебник / М.: КНОРУС, 2010. – 664 с.
   
4. 
   Иверсен В.Б. Разработка телетрафика и планирование сетей. Учеб. пособие. М.: Нац. Открытый Ун-т "ИНТУИТ": Бином. Лаборатория знаний, 2011.  526 с.
   
5. 
   Вадзинский P.H. Справочникповероятностнымраспределениям. – CП6.: Наука, 2001. – 295 с.
   
6. 
   Вишневский В.М. Теоретические основы проектирования компьютерных сетей // Москва: Техносфера, 2003. – 512 с.
   
7. 
   Кокорева, Е. В. Анализ сетей массового обслуживания [Электронный ресурс] : учебно-методическое пособие / Новосибирск : Сибирский государственный университет телекоммуникаций и информатики, 2015. — 39 c. — Режим доступа: http://www.iprbookshop.ru/55468.html по паролю.
   
8. 
   Башарин Г.П., Толмачев А.Л. Теория сетей массового обслуживания и ее приложения к анализу информационно-вычислительных систем [Электронный ресурс] // Итоги науки и техники : Сер. Теор. вероятн. Мат. стат. Теор. кибернет., 21, ВИНИТИ, М., 1983, С 3–119 – Режим доступа:http://www.mathnet.ru/links/4d33dbf1daca533be0933bb49245aa72/intv56.pdf