Решение систем линейных алгебраических уравнений методом простых итераций. Лабораторная работа 2. Лабораторная работа 2 Решение систем линейных алгебраических уравнений методом простых итераций
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Лабораторная работа №2 Решение систем линейных алгебраических уравнений методом простых итераций Вариант 25 Метод простых итераций используется для решения разряженных систем большой размерности, матрица которой должна быть близкой к диагональной. Основная формула метода 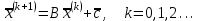 (Л7.1) (Л7.1)Если система линейных уравнений задана в традиционной форме 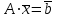 , ее сначала нужно привести к форме (Л7.1) методом Якоби. , ее сначала нужно привести к форме (Л7.1) методом Якоби.Задание № 1 Методом простых итераций с точностью 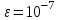 решить систему линейных алгебраических уравнений, заданную в форме решить систему линейных алгебраических уравнений, заданную в форме 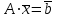 . . Н  Система линейных уравнений задана в традиционной форме 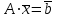 , ее сначала нужно привести к форме , ее сначала нужно привести к форме 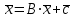 ( формула задается как ( формула задается как 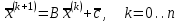 ) методом Якоби. ) методом Якоби.Находим c по формуле:    Для проверки решим эту же систему 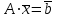 встроенной программой lsolve встроенной программой lsolve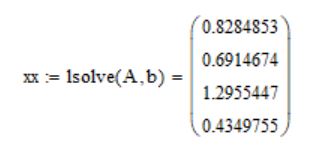 Возьмем в качестве начального приближения вектор 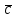 и узнаем сколько итераций потребуется для достижения заданной точности и узнаем сколько итераций потребуется для достижения заданной точности 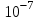 . . После приведения системы уравнений из вида 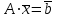 , к виду , к виду 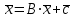 и вычисления k сам процесс последовательных приближений можно записать в векторно-матричной форме всего лишь одной строкой программы. и вычисления k сам процесс последовательных приближений можно записать в векторно-матричной форме всего лишь одной строкой программы. Вектор невязки:  Задание №2 С помощью метода прогонки найти решение системы, когда n =50. Применяя средства пакета MathCad и рекуррентные формулы решить систему линейных алгебраических уравнений с трехдиагональной основной матрицей. Найти вектор-невязки. N=25  Решение Метод прогонки является прямым и включает прямой и обратный ход. В течении прямого хода отыскиваются вспомогательные переменные (прогоночные коэффициенты). Обратный ход помогает найти значения неизвестных. 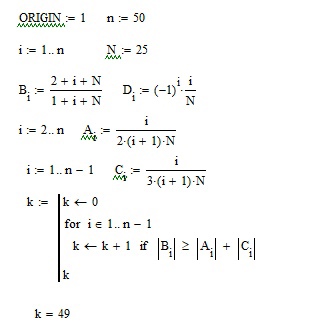 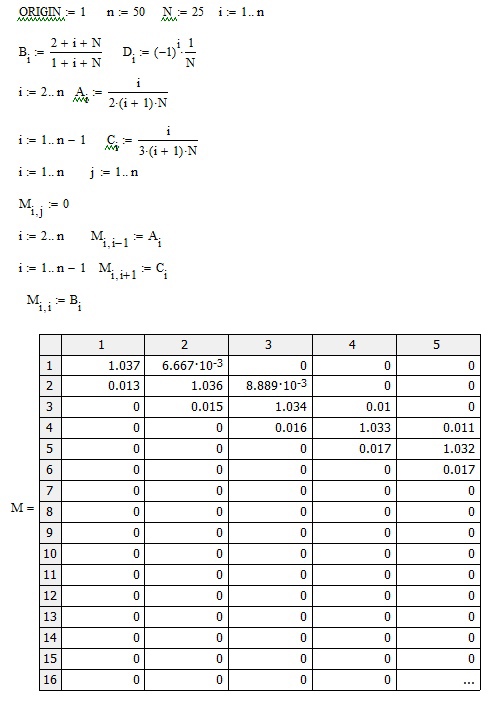 Трехдиагональная матрица М: верхняя диагональ - значения 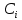 , средняя - значения , средняя - значения 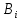 и нижняя диагональ - значения и нижняя диагональ - значения 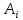 . .   Найдем вектор-столбец невязки:  |
