Уравнивание спутниковых измерений различными способами. вторая работа. Лабораторная работа 2 ст гр. 15Гео Гатченко П. Д. Проверил Дегтярев А. М. Новополоцк 2018
 Скачать 56.67 Kb. Скачать 56.67 Kb.
|
|
Министерство образования Республики Беларусь УО « Полоцкий государственный университет» Кафедра геодезии и Гис Лабораторная работа №2 Выполнила: ст.гр. 15-Гео Гатченко П.Д. Проверил: Дегтярев А.М. Новополоцк 2018 1. Уравнивание свободных спутниковых сетей на основе косвенной линейной формы параметрическим способом. Выбор оптимальной фиксации. Составляем новую матрицу весов Р2, в которой диагональные элементы изначальная матрица весов Р и Р1,где P1: 1000000 0 0 0 0 0 0 1000000 0 0 0 0 0 0 1000000 0 0 0 0 0 0 1000000 0 0 0 0 0 0 1000000 0 0 0 0 0 0 1000000 Получаем матрицу системы нормальных уравнение по формуле: 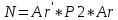 Получаем матрицу 12*12. Ранг матрицы коэффициентов нормальных уравнений N равен равен числу определяемых параметров . rank(N)=9 Число необходимых исходных элементов зависит от размерности задачи и типа измеренных величин. Это число часто называют дефектом N, который равен d =m-rank(N) d=12-9=3 из нее получаем матрицу Q. 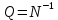 Получилась матрица 12*12 Columns 1 through 8 1.1033 0.1966 -0.0790 0.3896 0.1057 0.1346 0.0000 -0.0000 0.1966 0.8577 -0.0174 0.1003 0.2017 0.0729 0.0000 0.0000 -0.0790 -0.0174 0.9483 0.1273 0.0769 0.3125 -0.0000 -0.0000 0.3896 0.1003 0.1273 1.1124 0.1616 0.0364 0.0000 -0.0000 0.1057 0.2017 0.0769 0.1616 0.8689 0.1037 -0.0000 0.0000 0.1346 0.0729 0.3125 0.0364 0.1037 0.9426 0.0000 -0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 Columns 9 through 12 -0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 Проверка. Мы получили такие же элементы как матрица Q из прямого способа. Q = 1.1033 0.1966 -0.0790 0.3896 0.1057 0.1346 0.1966 0.8577 -0.0174 0.1003 0.2017 0.0729 -0.0790 -0.0174 0.9483 0.1273 0.0769 0.3125 0.3896 0.1003 0.1273 1.1124 0.1616 0.0364 0.1057 0.2017 0.0769 0.1616 0.8689 0.1037 0.1346 0.0729 0.3125 0.0364 0.1037 0.9426 Второй способ фиксации. Надо найти матрицу 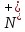 . .Первым шагом находим матрицуNпо формуле: 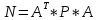 , где матрица А состоит из матрицы плана А и матрицы В, которую мы состояли по исходным пунктам. , где матрица А состоит из матрицы плана А и матрицы В, которую мы состояли по исходным пунктам.Columns 1 through 8 1.1177 -0.1860 0.2084 -0.3899 -0.0151 -0.1976 -0.3875 0.0699 -0.1860 1.2797 0.0514 -0.0151 -0.2692 -0.0592 0.0699 -0.3386 0.2084 0.0514 1.2469 -0.1976 -0.0592 -0.4330 0.0877 0.0067 -0.3899 -0.0151 -0.1976 1.0772 -0.1435 0.0966 -0.2866 0.1425 -0.0151 -0.2692 -0.0592 -0.1435 1.2580 -0.0903 0.1425 -0.5703 -0.1976 -0.0592 -0.4330 0.0966 -0.0903 1.2434 -0.0175 0.2425 -0.3875 0.0699 0.0877 -0.2866 0.1425 -0.0175 0.6741 -0.2123 0.0699 -0.3386 0.0067 0.1425 -0.5703 0.2425 -0.2123 0.9089 0.0877 0.0067 -0.4192 -0.0175 0.2425 -0.4230 -0.0702 -0.2493 -0.3403 0.1313 -0.0985 -0.4007 0.0161 0.1185 0 0 0.1313 -0.6720 0.0011 0.0161 -0.4185 -0.0930 0 0 -0.0985 0.0011 -0.3947 0.1185 -0.0930 -0.3874 0 0 Columns 9 through 12 0.0877 -0.3403 0.1313 -0.0985 0.0067 0.1313 -0.6720 0.0011 -0.4192 -0.0985 0.0011 -0.3947 -0.0175 -0.4007 0.0161 0.1185 0.2425 0.0161 -0.4185 -0.0930 -0.4230 0.1185 -0.0930 -0.3874 -0.0702 0 0 0 -0.2493 0 0 0 0.8422 0 0 0 0 0.7410 -0.1474 -0.0200 0 -0.1474 1.0904 0.0920 0 -0.0200 0.0920 0.7821 Матрица содержит ранговое и дефектное пространство. Ранговая часть – 9*12, дефектная 3*12. 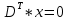 Из этого: 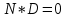 Здесь спрятан базис ноль пространства. 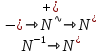 Когда выполняются все 4 условия, то можно получить 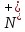 (псевдоподобнаяматрица Мура-Пенроуза). Она дает однозначное решение: (псевдоподобнаяматрица Мура-Пенроуза). Она дает однозначное решение: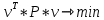 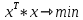 Cоставляем блочную матрицу N,состоящую из блоков : 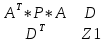 Где Dсостоит из D1 и D2: D1=[Z1 Z1 E1 Z1]T D2=[Z1 Z1Z1 E1]T  Z  1= 0 0 0 0 0 0 1= 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 N= Columns 1 through 8 1.1177 -0.1860 0.2084 -0.3899 -0.0151 -0.1976 -0.3875 0.0699 -0.1860 1.2797 0.0514 -0.0151 -0.2692 -0.0592 0.0699 -0.3386 0.2084 0.0514 1.2469 -0.1976 -0.0592 -0.4330 0.0877 0.0067 -0.3899 -0.0151 -0.1976 1.0772 -0.1435 0.0966 -0.2866 0.1425 -0.0151 -0.2692 -0.0592 -0.1435 1.2580 -0.0903 0.1425 -0.5703 -0.1976 -0.0592 -0.4330 0.0966 -0.0903 1.2434 -0.0175 0.2425 -0.3875 0.0699 0.0877 -0.2866 0.1425 -0.0175 0.6741 -0.2123 0.0699 -0.3386 0.0067 0.1425 -0.5703 0.2425 -0.2123 0.9089 0.0877 0.0067 -0.4192 -0.0175 0.2425 -0.4230 -0.0702 -0.2493 -0.3403 0.1313 -0.0985 -0.4007 0.0161 0.1185 0 0 0.1313 -0.6720 0.0011 0.0161 -0.4185 -0.0930 0 0 -0.0985 0.0011 -0.3947 0.1185 -0.0930 -0.3874 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 9 through 16 0.0877 -0.3403 0.1313 -0.0985 0 0 0 0 0.0067 0.1313 -0.6720 0.0011 0 0 0 0 -0.4192 -0.0985 0.0011 -0.3947 0 0 0 0 -0.0175 -0.4007 0.0161 0.1185 0 0 0 0 0.2425 0.0161 -0.4185 -0.0930 0 0 0 0 -0.4230 0.1185 -0.0930 -0.3874 0 0 0 0 -0.0702 0 0 0 1.0000 0 0 0 -0.2493 0 0 0 0 1.0000 0 0 0.8422 0 0 0 0 0 1.0000 0 0 0.7410 -0.1474 -0.0200 0 0 0 1.0000 0 -0.1474 1.0904 0.0920 0 0 0 0 0 -0.0200 0.0920 0.7821 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 Columns 17 through 18 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1.0000 0 0 1.0000 0 0 0 0 0 0 0 0 0 0 0 0 Из нее получаем матрицу Q. Она должна получится как Q в прошлом способе. Columns 1 through 8 1.1033 0.1966 -0.0790 0.3896 0.1057 0.1346 0 0 0.1966 0.8577 -0.0174 0.1003 0.2017 0.0729 0 0 -0.0790 -0.0174 0.9483 0.1273 0.0769 0.3125 0 0 0.3896 0.1003 0.1273 1.1124 0.1616 0.0364 0 0 0.1057 0.2017 0.0769 0.1616 0.8689 0.1037 0 0 0.1346 0.0729 0.3125 0.0364 0.1037 0.9426 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.5197 0.0191 -0.0815 0.4292 -0.0555 0.0318 1.0000 0 -0.0378 0.3599 -0.0569 -0.0692 0.5078 -0.1615 0 1.0000 -0.0931 -0.0467 0.5203 0.0141 -0.1424 0.4930 0 0 0.4803 -0.0191 0.0815 0.5708 0.0555 -0.0318 0 0 0.0378 0.6401 0.0569 0.0692 0.4922 0.1615 0 0 0.0931 0.0467 0.4797 -0.0141 0.1424 0.5070 0 0 Columns 9 through 16 0 0 0 0 0.5197 -0.0378 -0.0931 0.4803 0 0 0 0 0.0191 0.3599 -0.0467 -0.0191 0 0 0 0 -0.0815 -0.0569 0.5203 0.0815 0 0 0 0 0.4292 -0.0692 0.0141 0.5708 0 0 0 0 -0.0555 0.5078 -0.1424 0.0555 0 0 0 0 0.0318 -0.1615 0.4930 -0.0318 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -0.3354 0.0825 0.0247 0.3354 0 0 0 0 0.0825 -0.4454 0.0337 -0.0825 1.0000 0 0 0 0.0247 0.0337 -0.3723 -0.0247 0 1.0000 0 0 0.3354 -0.0825 -0.0247 -0.3354 0 0 1.0000 0 -0.0825 0.4454 -0.0337 0.0825 0 0 0 1.0000 -0.0247 -0.0337 0.3723 0.0247 Columns 17 through 18 0.0378 0.0931 0.6401 0.0467 0.0569 0.4797 0.0692 -0.0141 0.4922 0.1424 0.1615 0.5070 0 0 0 0 0 0 0 0 1.0000 0 0 1.0000 -0.0825 -0.0247 0.4454 -0.0337 -0.0337 0.3723 0.0825 0.0247 -0.4454 0.0337 0.0337 -0.3723 Ранг матрицы 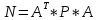 равен 9. Дефект 12-3=3. равен 9. Дефект 12-3=3.Вырезаем из этой матрицы следующие элементы: 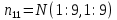 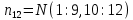 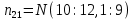 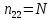 Находим Dпо формуле: 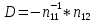 Составляем матрицу Dd = 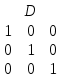 Далее составляем блочную матриц nсостоящую из блоков: 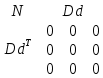 Находим обратну матрицу q= 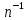 и вырезаем из нее следующие элементы (1:12,1:12). Получаем матрицу 12*12. и вырезаем из нее следующие элементы (1:12,1:12). Получаем матрицу 12*12.Псведоподобная матрица 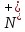 находится по формуле: находится по формуле: 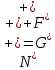 = =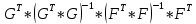 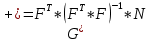 F вырезаем из N – (1:12,1:9) Получаем матрицу 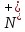 Columns 1 through 8 1.1177 -0.1860 0.2084 -0.3899 -0.0151 -0.1976 -0.3875 0.0699 -0.1860 1.2797 0.0514 -0.0151 -0.2692 -0.0592 0.0699 -0.3386 0.2084 0.0514 1.2469 -0.1976 -0.0592 -0.4330 0.0877 0.0067 -0.3899 -0.0151 -0.1976 1.0772 -0.1435 0.0966 -0.2866 0.1425 -0.0151 -0.2692 -0.0592 -0.1435 1.2580 -0.0903 0.1425 -0.5703 -0.1976 -0.0592 -0.4330 0.0966 -0.0903 1.2434 -0.0175 0.2425 -0.3875 0.0699 0.0877 -0.2866 0.1425 -0.0175 0.6741 -0.2123 0.0699 -0.3386 0.0067 0.1425 -0.5703 0.2425 -0.2123 0.9089 0.0877 0.0067 -0.4192 -0.0175 0.2425 -0.4230 -0.0702 -0.2493 -0.3403 0.1313 -0.0985 -0.4007 0.0161 0.1185 0 0 0.1313 -0.6720 0.0011 0.0161 -0.4185 -0.0930 0 0 -0.0985 0.0011 -0.3947 0.1185 -0.0930 -0.3874 0 0 1.0000 0.0000 -0.0000 1.0000 0.0000 0.0000 1.0000 0.0000 0.0000 1.0000 0 0.0000 1.0000 0.0000 0.0000 1.0000 -0.0000 0.0000 1.0000 -0.0000 0.0000 1.0000 -0.0000 -0.0000 Columns 9 through 15 0.0877 -0.3403 0.1313 -0.0985 1.0000 0.0000 -0.0000 0.0067 0.1313 -0.6720 0.0011 0.0000 1.0000 0.0000 -0.4192 -0.0985 0.0011 -0.3947 -0.0000 0 1.0000 -0.0175 -0.4007 0.0161 0.1185 1.0000 0.0000 -0.0000 0.2425 0.0161 -0.4185 -0.0930 0.0000 1.0000 0.0000 -0.4230 0.1185 -0.0930 -0.3874 0.0000 0.0000 1.0000 -0.0702 0 0 0 1.0000 0.0000 -0.0000 -0.2493 0 0 0 0.0000 1.0000 -0.0000 0.8422 0 0 0 0.0000 0.0000 1.0000 0 0.7410 -0.1474 -0.0200 1.0000 0 0 0 -0.1474 1.0904 0.0920 0 1.0000 0 0 -0.0200 0.0920 0.7821 0 0 1.0000 0.0000 1.0000 0 0 0 0 0 0.0000 0 1.0000 0 0 0 0 1.0000 0 0 1.0000 0 0 0 Использование сингулярного разложения. Приводим матрицу Nк диагональному виду: 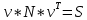 v -собственный вектор S – собственные значения. Использовав следующие свойства: 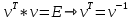 , мы получаем , мы получаем 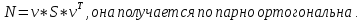 Длина каждого вектор равна 1. Ортономированные базисы спрятаны в 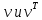 . .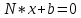 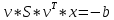 В матрице Sстолько диагональных нулей, сколько равен дефект. Если дефекта нет, то 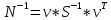 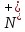 можно получить заменив можно получить заменив 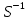 на на 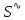 . .Находим базис рангового пространства N. Columns 1 through 8 1.1177 -0.1860 0.2084 -0.3899 -0.0151 -0.1976 -0.3875 0.0699 -0.1860 1.2797 0.0514 -0.0151 -0.2692 -0.0592 0.0699 -0.3386 0.2084 0.0514 1.2469 -0.1976 -0.0592 -0.4330 0.0877 0.0067 -0.3899 -0.0151 -0.1976 1.0772 -0.1435 0.0966 -0.2866 0.1425 -0.0151 -0.2692 -0.0592 -0.1435 1.2580 -0.0903 0.1425 -0.5703 -0.1976 -0.0592 -0.4330 0.0966 -0.0903 1.2434 -0.0175 0.2425 -0.3875 0.0699 0.0877 -0.2866 0.1425 -0.0175 0.6741 -0.2123 0.0699 -0.3386 0.0067 0.1425 -0.5703 0.2425 -0.2123 0.9089 0.0877 0.0067 -0.4192 -0.0175 0.2425 -0.4230 -0.0702 -0.2493 -0.3403 0.1313 -0.0985 -0.4007 0.0161 0.1185 0.0000 0.0000 0.1313 -0.6720 0.0011 0.0161 -0.4185 -0.0930 -0.0000 0.0000 -0.0985 0.0011 -0.3947 0.1185 -0.0930 -0.3874 -0.0000 -0.0000 Columns 9 through 12 0.0877 -0.3403 0.1313 -0.0985 0.0067 0.1313 -0.6720 0.0011 -0.4192 -0.0985 0.0011 -0.3947 -0.0175 -0.4007 0.0161 0.1185 0.2425 0.0161 -0.4185 -0.0930 -0.4230 0.1185 -0.0930 -0.3874 -0.0702 0.0000 -0.0000 -0.0000 -0.2493 0.0000 0.0000 -0.0000 0.8422 0.0000 -0.0000 -0.0000 0.0000 0.7410 -0.1474 -0.0200 -0.0000 -0.1474 1.0904 0.0920 -0.0000 -0.0200 0.0920 0.7821 Потом получаем S по формуле: 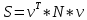 Берем диагональные элементы из S и вырезаем из них элементы (1:9). 2.2306 2.0603 1.8163 1.5692 1.2812 1.2358 0.8406 0.7057 0.5220 Получаем матрицу S1.  Далее находим N1 по формуле: 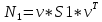 Columns 1 through 8 0.5610 0.0868 -0.0998 -0.1818 0.0125 0.0997 -0.1515 -0.0623 0.0868 0.4872 -0.0329 0.0039 -0.2067 0.0562 -0.0332 -0.2588 -0.0998 -0.0329 0.4905 0.1032 0.0372 -0.1644 -0.1089 -0.0235 -0.1818 0.0039 0.1032 0.5678 0.0623 -0.0295 -0.2926 -0.0967 0.0125 -0.2067 0.0372 0.0623 0.5002 0.0206 -0.1107 -0.1243 0.0997 0.0562 -0.1644 -0.0295 0.0206 0.5005 0.0009 -0.1534 -0.1515 -0.0332 -0.1089 -0.2926 -0.1107 0.0009 1.0401 0.2609 -0.0623 -0.2588 -0.0235 -0.0967 -0.1243 -0.1534 0.2609 0.8336 -0.0971 -0.0208 -0.1493 -0.0037 -0.1595 -0.1900 0.1520 0.2221 -0.2277 -0.0576 0.1055 -0.0933 0.0359 -0.0711 -0.5960 -0.1018 -0.0369 -0.0216 0.0192 0.0305 -0.1691 0.0766 -0.1170 -0.4505 0.0971 -0.0026 -0.1768 -0.0700 0.1017 -0.1462 -0.0439 -0.0451 Columns 9 through 12 -0.0971 -0.2277 -0.0369 0.0971 -0.0208 -0.0576 -0.0216 -0.0026 -0.1493 0.1055 0.0192 -0.1768 -0.0037 -0.0933 0.0305 -0.0700 -0.1595 0.0359 -0.1691 0.1017 -0.1900 -0.0711 0.0766 -0.1462 0.1520 -0.5960 -0.1170 -0.0439 0.2221 -0.1018 -0.4505 -0.0451 0.8553 -0.0511 -0.0417 -0.5161 -0.0511 0.9170 0.1235 0.0168 -0.0417 0.1235 0.6413 -0.0540 -0.5161 0.0168 -0.0540 0.8391 b находим по формуле: 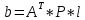 lиз косвенного способа. b= 0.0009 -0.0052 0.0006 0.0002 -0.0043 0.0070 0.0009 0.0042 -0.0034 -0.0019 0.0053 -0.0042  -0.0004 0.0022 -0.0000 0.0005 0.0024 -0.0043 -0.0027 -0.0018 0.0005 0.0025 -0.0028 0.0037 Находим приближенные значения  . .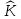 = = 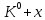 Где 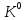 координаты всех пунктов. координаты всех пунктов.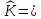 1178261.8278 -4365847.1341 -3537042.6485 1178805.8165 -4365241.5712 -3537065.2559 1179149.6105 -4366386.5338 -3537010.2819 1177393.8825 -4365567.0106 -3537040.0854 Далее находим поправки v. 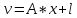 v= -0.0023 -0.0040 0.0006 -0.0010 -0.0021 0.0052 -0.0020 0.0052 -0.0080 0.0040 0.0034 0.0007 -0.0033 -0.0028 0.0068 Получаем приближенные значения  . .758,8929 -442,7465 -2,0233 539,5442 608,8871 -1,2691 1407,4913 328,7820 -15,8387 219,3487 -1051,6336 -0,7542 867,9471 -280,1051 -14,5696 Теперь по  Выполняем сначала в ручную, а потом по формуле Выполняем сначала в ручную, а потом по формуле 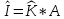 758,8929 -442,7465 -2,0233 539,5442 608,8871 -1,2691 1407,4913 328,7820 -15,8387 219,3487 -1051,6336 -0,7542 867,9471 -280,1051 -14,5696 Все вычисления выполнены правильно. В итоге мы получили конечный результат вычисления и приступаем к оценке точности. 2. Оценка точности уравнивания несвободных и свободных спутниковых сетей параметрическим способом. Результаты уравнивания характеризуются двумя сторонами: количество и качество. Есть волнаfи ее характеристика σf(mf) –точечная оченка. a≤Хист ≤ b – интервальная оценка. Говорят, что Хист находится в интервале от а до bс вероятностью Р. Сплошная оценка – оценка всех величин в сети. Локальная оценка – оценка элемента сети. Глобальная оценка – оценка всего построения сети. Относительная ошибка - погрешность одного пункта относительного другого, если они оба определяемые. Абсолютная ошибка – относительно всех исходных. Точечная абсолютная оценка. Находим оценку для 2 пунктов: 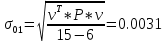 Находим оценку для 4 пунктов: 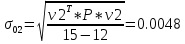 Находи след ковариационной матриц K(обобщенную абсолютную погрешность сети), где K вычисляется по формуле: 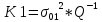 Ее след равен 5.4293*10-5 Находим определитель этой же матрицы (Обобщенную относительную погрешность сети). Определитель равен 3.3890*10-31, т.е. равен 0. Находим след ковариационной матрицы 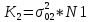 След равен 0.0002 Определитель равен 0. Находим погрешности в пункты k1и k2. k1равен корню квадратному из диагональных элементов матрицы K1. k2равен корню квадратному из диагональных элементов матрицы К2. k1 0.0032 0.0028 0.0030 0.0032 0.0028 0.0030 k2 0.0036 0.0034 0.0034 0.0036 0.0034 0.0034 0.0049 0.0044 0.0045 0.0046 0.0039 0.0044 Sp1= 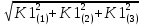 = 0.0052 = 0.0052Sp2= 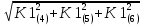 = 0.0052 = 0.0052Sp3= 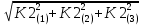 = 0.0060 = 0.0060Sp4= 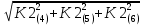 = 0.0060 = 0.0060Sp5= 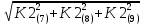 = 0.0080 = 0.0080Sp6= 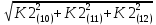 = 0.0075 = 0.0075Относительная оценка. Создаем матрицу F1 состоящая из –E и E, где E = 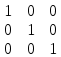 . .Дальше находим матрицу K по формуле: 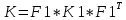 1.0e-04 * 0.1337 0.0142 -0.0283 0.0142 0.1231 -0.0059 -0.0283 -0.0059 0.1178 И выбираем из нее диагональные элементы. 1.0e-04 * 0.1337 0.1231 0.1178 Находим sp1= 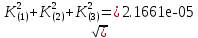 Далее находим матрицу k3 путем вырезания из матрицы K2 элементы (1:6,1:6). Находим матрицу K3 по формуле: 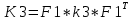 1.0e-04 * 0.3482 0.0310 -0.0775 0.0310 0.3268 -0.0247 -0.0775 -0.0247 0.3079 И выбираем из нее диагональные элементы. 1.0e-04 * 0.3482 0.3268 0.3079 Находим sp2= 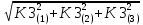 = 5.6822e-05 = 5.6822e-053.Эллипсоид погрешностей. Способы получения и использования. Основа квадратичной формы – матрицы 3*3. Собственные значения связаны с собственными векторами. Начинаем с нахождения собственных значений. Создаем матрицу К4, вырезая из матрицы К1 элементы (1:3,1:3), и матрицу К5, вырезая из матрицы К1 элементы (4:6,4:6). K4= 1.0e-04 * 0.1027 0.0183 -0.0074 0.0183 0.0798 -0.0016 -0.0074 -0.0016 0.0883 K5= 1.0e-04 * 0.1035 0.0150 0.0034 0.0150 0.0809 0.0097 0.0034 0.0097 0.0877 Находим вектор v1: -0.8497 0.1708 -0.4988 -0.4568 0.2339 0.8583 0.2633 0.9571 -0.1207 Получаем s1 по формуле: 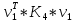 1.0e-04 * 0.1148 -0.0000 -0.0000 0 0.0866 0.0000 -0.0000 -0.0000 0.0694 Находим значения большой, средней и малой оси по формуле: 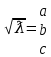 Где a,b,c – оси ƛ равняется квадратному корню из диагональных элементов s1. Взяв квадратный корень из ƛ получаем значения осей: a= 0.0034 b= 0.0029 c= 0.0026 Находим значение этих осей по 2 способу. Det(K-ƛE)=0 Det(K-ƛE)*v=0, где ƛ собственные значения (оси), v- собственные вектора (ориентировка). В матрице К4 от диагональных элементов отнимаем ƛ, берем определитель и приравниваем к нулю. Получаем: 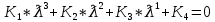 (1) (1)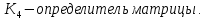 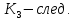 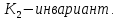 По формуле K5=poly(K4) мы получим значения всех 4 коэффициентов. Решаем кубическое уравнение (1) и получаем значение осей: ƛ=roots(K5) Берем квадратный корень из ƛ и получаем значения осей. a=0.0034 b=0.0029 c=0.0026 Координаты осей сошлись с первым способом. Для 2 пункта. Аналогично создаем вектор v2 из K5 и по формуле 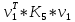 получаем s2. получаем s2.v2 = -0.8323 0.4357 0.3427 -0.4728 -0.2355 -0.8491 -0.2892 -0.8688 0.4020 s2 = 1.0e-04 * 0.1133 0 0 -0.0000 0.0887 -0.0000 -0.0000 0.0000 0.0702 Находим ƛ и следом значения осей. a=0.0034 b=0.0030 c=0.0027 Находим значения осей для этого пункта 2 способ. К6=poly(K5) ƛ=roots(K6) a=0.0034 b=0.0030 c=0.0027 Значения осей в 2 способах сошлись. Находим значения для 3 пункта. Из матрицы k3 вырезаем элементы (1:3,1:3) и получаем матрицу k. Находим значения v3 и s3. v3 = -0.7573 0.0359 0.6521 -0.4351 -0.7723 -0.4629 0.4870 -0.6343 0.6005 s3 = 1.0e-04 * 0.1575 0 0.0000 0 0.1064 -0.0000 0 0.0000 0.0951 Находим ƛ и значения осей. a=0.0040 b=0.0033 c=0.0031 2 способ для этого пункта. k1 = poly(k) ƛ=roots(k1) a=0.0040 b=0.0033 c=0.0031 Находим значения осей для 4 пункта. Из матрицы k3 вырезаем элементы (4:6,4:6)и получаем матрицу k2. Находим значения v4и s4. v4 = -0.8665 0.1368 0.4800 -0.4768 -0.5114 -0.7150 0.1477 -0.8484 0.5083 s4 = 1.0e-04 * 0.1416 -0.0000 -0.0000 -0.0000 0.1208 0.0000 -0.0000 0.0000 0.1035 Находим ƛ и значения осей. a=0.0038 b=0.0035 c=0.0032 2 способ для этого пункта. k5 = poly(k2) ƛ=roots(k5) a=0.0038 b=0.0035 c=0.0032 Представление. Находим для v1углы Эйлера v1_1 = 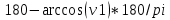 31.82 99.84 60.08 62.82 103.53 149.12 105.26 163.16 83.07 Далее берем косинусы значений большой оси и переводим: 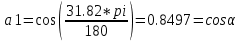 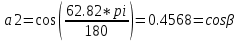 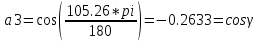 Находим длину: 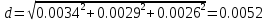 Где 0,0056 0,0049 0,0046 значения осей для 1 пункта. Находи погрешности пункта по осям эллипсоида: 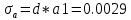 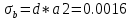 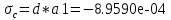 Аналогично для v2 находим углы Эйлера, берм косинусу значения большой оси, находим длину и погрешности пункта по осям эллипсоида: v2_2 = 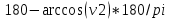 33.66 115.83 110.04 61.78 76.38 31.88 73.19 29.68 113.70 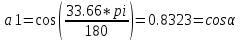 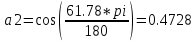 =cosβ =cosβ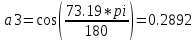 =cosγ =cosγ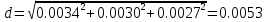 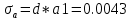 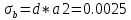 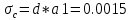 Для v3: V3_3= 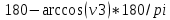 40.77 92.06 130.70 64.21 39.44 62.43 119.14 50.63 126.90 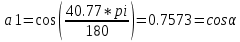 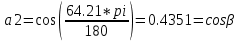 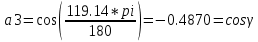 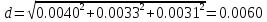 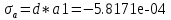 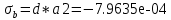 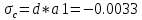 Находим ориентировку большой оси эллипсоида в нормальном (сферическом представлении) s, φ, ƛ. S1=d1=0.0052 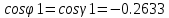 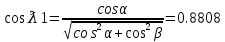 Отсюда ƛ1=arccos(0.8808)=28.26° Обратная задача V1*S2*V1т=K1 K1=1.0353e-05 V2*S2*V2т=K2 K2= 8.0868e-06 Получаем такие же значения как в матрице K5 по диагонали. K5= 1.0e-04 * 0.1035 0.0150 0.0034 0.0150 0.0809 0.0097 0.0034 0.0097 0.0877 |
