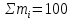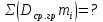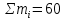|
|
лаб.раб.. Лаб Раб ТМ №2. Лабораторная работа 2 Статистический метод исследования точности обработки на настроенном станке Цель работы
ЛАБОРАТОРНАЯ РАБОТА № 2
Статистический метод исследования точности обработки
на настроенном станке
Цель работы:
-
Произвести математическую обработку результатов измерения партии деталей для определения меры рассеяния размеров партии деталей.
-
Построить кривые фактического и нормального распределения размеров.
Применяемое оборудование, приспособления и инструменты:
-
рабочий чертеж (или эскиз) детали;
-
образцы деталей, предварительно обработанных (не менее 50 шт.) или данные об их замерах по диаметру;
-
измерительный инструмент – микрометр 0 – 25 (цена деления 0,01 мм) со стойкой;
-
справочники и справочные пособия.
Порядок выполнения работы:
-
Обмер деталей партии по рассматриваемому параметру и внесение
результатов в графы 1, 2 и 3 таблицы 1 (или использование готовых данных из этих граф).
-
Расчет данных и заполнение граф 4 – 8 таблицы 1.
-
Расчет меры рассеивания и установление возможности брака.
-
Определение среднего арифметического значения размера.
-
Определение среднего квадратичного отклонения – величины погрешности.
-
Построение графиков фактического и нормального распределения.
-
Расчет процента брака исправимого и неисправимого, а также процента выхода годных деталей.
-
Выводы о качестве наладки станка и рекомендации по ее улучшению.
Содержание отчета:
-
Наименование работы;
-
Цель работы;
-
Исходные данные (согласно варианта).Данные об измерительных средствах (наименование, тип, цена деления);
-
Эскиз детали;
-
Составление таблицы интервалов, частости, квадратичных отклонений;
-
Построение кривых фактического и нормального распределения с расчетами;
-
Выводы и предложения.
Пример выполнения лабораторной работы
(вариант №1, первая размерная группа)
-
Исходные данные
Вариант № 1
В порядке анализа точности обработки деталей по наружной цилиндрической поверхностиØ12-0,07 на станке обработана партия деталей (рис. 1) в количестве 100 штук и произведены замеры исследуемого размера. Детали партии обработаны при одной настройке станка без смены и переналадки инструмента. Контролируемый размер измеряли микрометром и результаты измерений распределили по размерным группам с интервалом в 0,01 мм. Таких групп получилось 11.
Эти исходные данные внесены в графы 1,2,3 таблицы 1.
Таблица 1 – Результаты обмера и расчета
Исходные данные
|
Расчетные данные
|
Номер размерной группы
|
Интервалы размеров в группе
D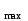 , D , D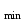 , мм , мм
|
Число деталей в группе
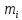 , шт. , шт.
|
Средний размер группы
(в интервале)
Dср.гр , мм
|
Произведение данных по графам 3 и 4
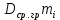 , мм , мм
|
Отклонение среднего размера группы от среднего арифметического
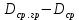 , мм , мм
|
Квадратичное отклонение среднего размера группы от среднего арифметического
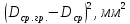
|
Произведение квадратичного отклонения на числодеталей
в размерной группе
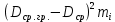 , мм2 , мм2
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
1
|
11,91-11,92
|
1
|
11,915
|
11,915
|
-0,0506
|
25,6036 10-4 10-4
|
25,6036 10-4 10-4
|
2
|
11,92-11,93
|
2
|
|
|
|
|
|
3
|
11,93-11,94
|
8
|
|
|
|
|
|
4
|
11,94-11,95
|
13
|
|
|
|
|
|
5
|
11,95-11,96
|
15
|
|
|
|
|
|
6
|
11,96-11,97
|
17
|
|
|
|
|
|
7
|
11,97-11,98
|
19
|
|
|
|
|
|
8
|
11,98-11,99
|
14
|
|
|
|
|
|
9
|
11,99-12,00
|
8
|
|
|
|
|
|
10
|
12,00-12,01
|
2
|
|
|
|
|
|
11
|
12,01-12,02
|
1
|
|
|
|
|
|
|
|
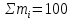
|
|
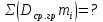
|
|
|
Итого: ?
|
Вариант № 2
В порядке анализа точности обработки деталей по наружной цилиндрической поверхностиØ15 -0,12 на станке обработана партия деталей (рис. 1) в количестве 60 штук и произведены замеры исследуемого размера. Детали партии обработаны при одной настройке станка без смены и переналадки инструмента. Контролируемый размер измеряли микрометром и результаты измерений распределили по размерным группам с интервалом в 0,02 мм. Таких групп получилось 10.
Эти исходные данные внесены в графы 1,2,3 таблицы 2.
Таблица 2 – Результаты обмера и расчета
Исходные данные
|
Расчетные данные
|
Номер размерной группы
|
Интервалы размеров в группе
D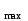 , D , D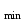 , мм , мм
|
Число деталей в группе
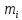 , шт. , шт.
|
Средний размер группы
(в интервале)
Dср.гр , мм
|
Произведение данных по графам 3 и 4
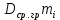 , мм , мм
|
Отклонение среднего размера группы от среднего арифметического
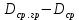 , мм , мм
|
Квадратичное отклонение среднего размера группы от среднего арифметического
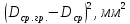
|
Произведение квадратичного отклонения на числодеталей
в размерной группе
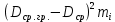 , мм2 , мм2
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
1
|
14,84 – 14,86
|
3
|
|
|
|
|
|
2
|
14,86 – 14,88
|
4
|
|
|
|
|
|
3
|
14,88 – 14,90
|
6
|
|
|
|
|
|
4
|
14,90 – 14,92
|
13
|
|
|
|
|
|
5
|
14,92 – 14,94
|
11
|
|
|
|
|
|
6
|
14,94 – 14,96
|
10
|
|
|
|
|
|
7
|
14,96 – 14,98
|
5
|
|
|
|
|
|
8
|
14,98 – 15,00
|
4
|
|
|
|
|
|
9
|
15,00 – 15,02
|
2
|
|
|
|
|
|
10
|
15,02 – 15,04
|
2
|
|
|
|
|
|
|
|
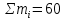
|
|
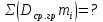
|
|
|
Итого: ?
|
Рисунок 1 Эскиз детали
-
Математическая обработка
-
Определяем меру рассеивания Мр , мм по формуле:
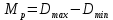
где М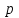 - мера рассеивания, мм; - мера рассеивания, мм;
D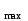 - наибольший размер детали из контролируемой партии, мм; - наибольший размер детали из контролируемой партии, мм;
D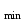 - наименьший размер детали из контролируемой партии, мм. - наименьший размер детали из контролируемой партии, мм.
Мр = 12,02 – 11,91 = 0,11
Так как мера рассеивания превышает допуск размера, следовательно при
обработке имеет место брак.
-
Определяем среднее арифметическое значение размера каждой размерной группы Dср.гр, мм:
Dср.гр = 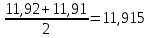
Результаты расчета вносим в графу 4 таблицы 1.
-
Определяем средний арифметический размер всех деталей партии Dср, мм по формуле:
Dср = 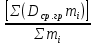 , ,
где mi - количество деталей в размерной группе, шт;
Σmi - количество деталей в контрольной партии, шт.
Числителем этой дроби является сумма данных графы 5 таблицы 1, а знаменателем – сумма данных графы 3 этой же таблицы.
В данном примере: Dср = 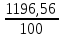 = 11,9656 мм. = 11,9656 мм.
-
Определяем среднее квадратичное отклонение σ, мм2:
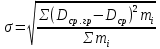 , ,
где числителем дроби под корнем является сумма данных приведенных в графе 8 таблицы 1.
Для группы 1 получены следующие данные:
- в графе 6: 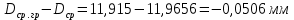 ; ;
- в графе 7: 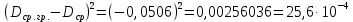
- в графе 8: 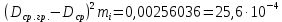
Аналогично выполняется расчет для всех размерных групп
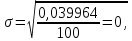 01999899 01999899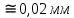
Принимаем σ = 0,02 мм
-
|
|
|
 Скачать 83.84 Kb.
Скачать 83.84 Kb.
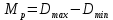
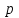 - мера рассеивания, мм;
- мера рассеивания, мм;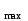 - наибольший размер детали из контролируемой партии, мм;
- наибольший размер детали из контролируемой партии, мм;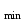 - наименьший размер детали из контролируемой партии, мм.
- наименьший размер детали из контролируемой партии, мм.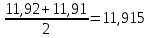
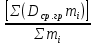 ,
,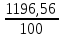 = 11,9656 мм.
= 11,9656 мм.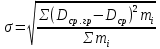 ,
,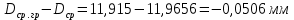 ;
;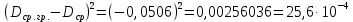
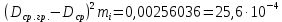
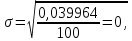 01999899
01999899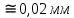

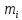 , шт.
, шт.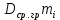 , мм
, мм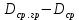 , мм
, мм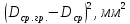
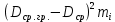 , мм2
, мм2 10-4
10-4