Лаба по оту. Лаб.р-та №2 2020 дист.об.. Лабораторная работа 2. Устойчивость линейных систем со сосредоточенными и постоянными параметрами

• Название: Лабораторная работа 2. Устойчивость линейных систем со сосредоточенными и постоянными параметрами
• Анкор: Лаба по оту
• Дата: 19.03.2022
• Размер: 217.5 Kb.
• Имя файла: Лаб.р-та №2 2020 дист.об..doc
• Тип: Лабораторная работа; #403781

Лабораторная работа №2.

Устойчивость линейных систем со сосредоточенными и постоянными параметрами.

Цель работы: изучить методы исследования устойчивости линейных систем со сосредоточенным и постоянными параметрами.

Постановка задачи.

Задана структурная схемы исследуемой системы вида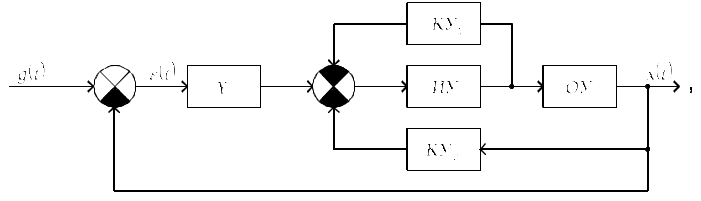

где У – усилительное звено с передаточной функцией ;

ИУ – исполнительное устройство с передаточной функций ;

ОУ – объект управления с передаточной функцией или



КУ₁ – первое корректирующее устройство с передаточной функцией ;

КУ₂ – второе корректирующее устройство с передаточной функцией и параметры передаточных функций ИУ и ОУ.
Требуется:

С помощью заданного критерия устойчивости (Гурвица, Рауса, Михайлова, Найквиста по АФЧХ, Найквиста по ЛАЧХ и ЛФЧХ) определить, при каких значениях К_у система при К₁ =К₂ =0 находится на апериодической и колебательной границах устойчивости, т.е. К_уа и К_ук соответственно.

Порядок выполнения работы.

1. 
   Определить с помощью заданного преподавателем критерия устойчивости все возможные критические значения коэффициента передачи усилителя К_уа и К_ук, при которых нескорректированная система замкнутого типа оказывается на границе апериодической и колебательной устойчивости соответственно. Каждый студент производит расчёт по заданному ему критерию для двух вариантов ОУ:
   

1-ый вариант ;

2-ой вариант

2. 
   Записать передаточные функции замкнутой системы при:
   

К_у=0,9К_ук;

К_у=К_ук;

К_у=1,1К_ук,
построить переходные процессы h(t) и вычислить полюса λ_i с помощью программы pp.exe в среде ДОС, « ТАУ++» или программы в среде Matlab.

3. 
   Построить АФЧХ, ЛАЧХ и ЛФЧХ для разомкнутой СУ при различных значениях Ку (см. п.2 ) для двух вариантов передаточных функций ОУ с помощью программы chast.exe в среде ДОС, «ТАУ++» или программы в среде Matlab.
   

Содержание отчёта.

1. 
   Название работы.
   
2. 
   Цель работы.
   
3. 
   Постановка задачи.
   
4. 
   Схема системы и данные задания.
   
5. 
   Расчётная часть по вычислению критических параметров системы (К_уа и К_ук) с использованием заданного критерия устойчивости с комментариями двух вариантов ОУ.
   
6. 
   Вывод передаточных функций замкнутой системы для двух вариантов ОУ и различных значениях К_у. Распечатки графиков переходных процессов h(t) и полюсов λ_i для различных значений К_у, при которых исследуемая система имеет различные передаточные функции.
   
7. 
   Передаточные функции разомкнутой системы и распечатки графиков АФЧХ,ЛАЧХ и ЛФЧХ при различных значениях Ку..
   
8. 
   Выводы по работе.
   

Вопросы для самопроверки.

1. 
   Что такое устойчивость линейных стационарных систем?
   
2. 
   Как определяется устойчивость линейных стационарных систем?
   
3. 
   Как определяется устойчивость системы по критерию Гурвица?
   
4. 
   Как определяется устойчивость системы по критерию Рауса?
   
5. 
   Как определяется устойчивость системы по критерию Михайлова?
   
6. 
   Как определяется устойчивость системы с помощью следствия из критерия Михайлова?
   
7. 
   Как определяется устойчивость замкнутой системы по критерию Найквиста с помощью АФЧХ?
   
8. 
   Как определяется устойчивость замкнутой системы по критерию Найквиста с помощью ЛАЧХ и ЛФЧХ?
   
9. 
   Как определить запасы устойчивости системы на амплитуде и фазе с помощью критерия Найквиста?
   
10. 
    Как определяются критические параметры системы с помощью известных критериев устойчивости?
    
11. 
    Как определяется устойчивость исследуемой системы по достаточным условиям устойчивости Соколова-Липатова?
    
12. 
    Граница устойчивости.
    
13. 
    Апериодическая граница устойчивости.
    
14. 
    Колебательная граница устойчивости.
    
15. 
    Как должны располагаться полюса передаточной функции СУ, находящейся на апериодической границе устойчивости?
    
16. 
    Как должны располагаться полюса передаточной функции СУ, находящейся на колебательной границе устойчивости?
    

Технические и другие средства обучения.

1. 
   Компьютер (ПЭВМ).
   
2. 
   Программа chast.exe и pp.exe в среде ДОС или программы в среде Matlab.
   
3. 
   Плакаты.
   
4. 
   Описания лабораторных работ.
   

Структурная схема системы управления
У ИУ ОУ
g(t) ε(t) x(t)

─