Ит. Лабораторные. Лабораторная работа 2 Задание 1
 Скачать 249.5 Kb. Скачать 249.5 Kb.
|
|
Лабораторная работа № 1 Основы работы с MATHCAD Задание 1 Задание 2  Задание 3 Задание 4 Задание 5   Задание 6 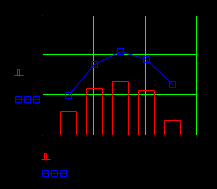 X-Y Plot Задание 7 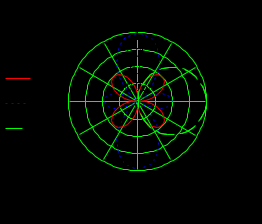 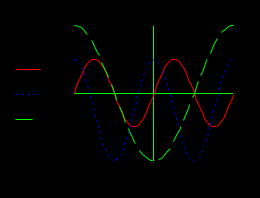 Задание 8   Surface Plot Surface Plot Contour Plot 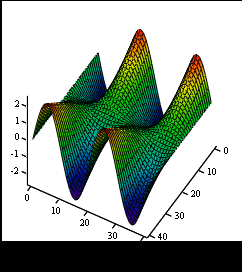 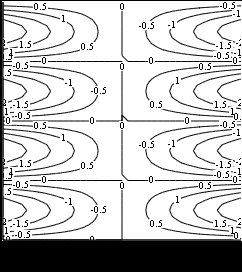 Задание 9 Лабораторная работа №2 Задание 1. Локализовать корни уравнения и вычислить значение одного корня методом Ньютона с точностью Е = 10-4. 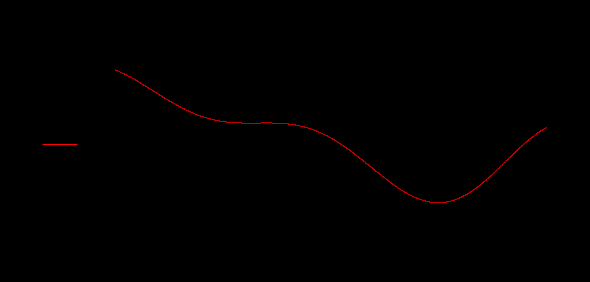 Начальные значения    Решение уравнений 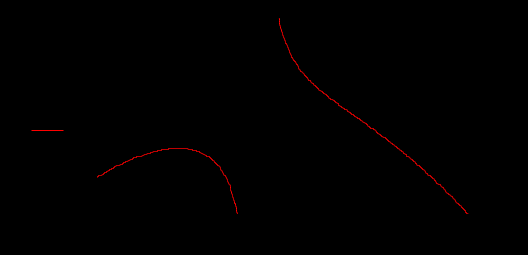 Начальные значения   Задание 2. Локализовать корни уравнения и вычислить значение одного корня методом бисекций с точностью Е = 10-4. Задание 3. Локализовать корни уравнения и вычислить значение одного корня методом итераций с точностью Е = 10-4 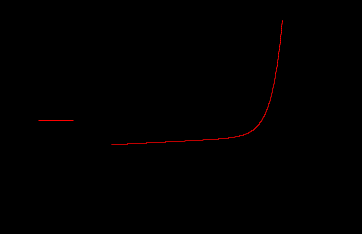 Будем искать корень уравнения, нахдящийся на отрезке локализации [0, 5] Приведем уравнение к виду х=xf(x), где итерационная функция (x)=xf(x), итерационный параметр  График производной f1(x) Максимальное и минимальное значения производной на концах отрезка 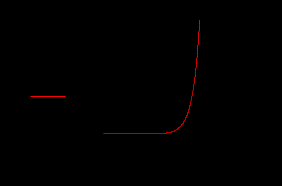   Лабораторная работа №3. Интегрирование функций. Задание 1. Составить программу для вычисления интеграла методом прямоугольников с точностью e = 10-4. Границы интегрирования А=1 - верхняя, В=2 - нижняя, число отрезков деления N=13. Исходные данные:  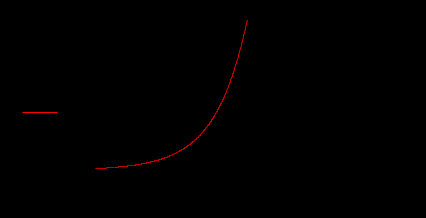  Задание №2 Составить программу для вычисления интегорала методом Симпсона с точностью = 10-4. Границы интегрирования А=2,2 - верхняя, В=2,8 - нижняя, число отрезков деления N=12.  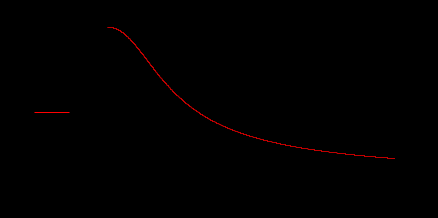  Задание 3. Составить программу для вычисления интегорала методом трапеций с точностью = 10-4. Границы интегрирования А=0,4 - верхняя, В=0,7 - нижняя, число отрезков деления N=11.  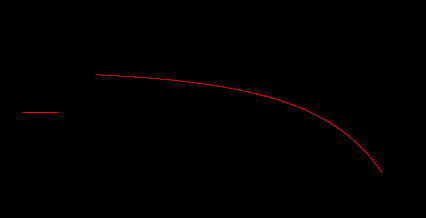  Лабораторная работа №4 Аппроксимация функций. Задание. По табличным данным построить график и определить вид эмпирической зависимости функции. Аппроксимировать функцию методом наименьших квадратов, найти числовые значения параметров. разработать программу для вычисления параметров функции. Исходные данные:   Решение задачи: Функция mnk, строящая многочлен степени m по методу наименьших квадратов, возвращает вектор a коэффициентов многочлена: Функция mnk, строящая многочлен степени m по методу наименьших квадратов, возвращает вектор a коэффициентов многочлена:  - формирование вектора правой части и матрицы нормальной системы Ga=b метода наименьших квадратов (базисные функции - 1, x, , - встроенная функция MATHCAD, решает систему линейных алгебраических уравнений Ga=b Входные параметры: x, y - векторы исходных данных; n+1 - размерность x,y. m+1 - количество возвращаемых коэффициентов Вычисление коэффициентов многочленов степени 0,1,2 по методу наименьших квадратов:   Функция P возвращает значение многочлена степени m в точке t; многочлен задается с помощью вектора коэффициентов a:  Графики многочленов степени 0,1,2 и точечный график исходной функции: 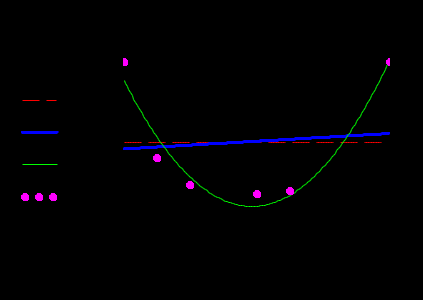 Вывод: функция имеет степенную зависимость. |
