Лабораторная работа по ОТС номер 22. Лабораторная работа 22 "Прохождение периодических сигналов через нелинейную цепь." Выполнил студент группы брт1801 Везарко Д. А
 Скачать 174.51 Kb. Скачать 174.51 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ (МТУСИ) Лабораторная работа №22 “Прохождение периодических сигналов через нелинейную цепь.” Выполнил студент группы БРТ1801: Везарко Д.А. Бригада №2 Москва 2020 Цель работы: Исследование формы и спектра тока на выходе резистивного нелинейного элемента при гармоническом входном напряжении. Схема эксперимента  2. ДОМАШНЕЕ ЗАДАНИЕ. Вариант № 2. Исходные данные: ВАХ нелинейного элемента
ВАХ диода 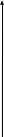 I,мА I,мА  5 5  4 4 3 3 2 2 1 1           0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 5 E, В Найдем параметры аппроксимирующей прямой: 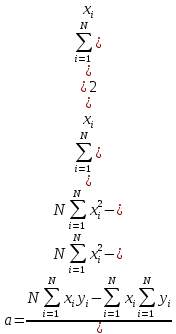 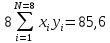 ; ; 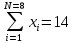 ; ; 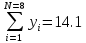 ; ;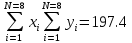 ; ; 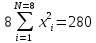 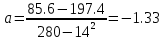 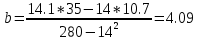 y=-1,33x+4,09 - аппроксимирующая прямая. U0= b/a = 4,09/1,33 3,075 В - напряжение отсечки S = a - 1,33 мА/В - крутизна аппроксимирующей прямой. Аппроксимирующая ВАХ имеет вид: 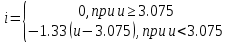 Амплитуда входного сигнала: Um=U0/2=1,53 В; Расчет значений напряжений смещения и амплитуд гармоник. Уравнение для угла отсечки имеет вид: 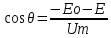 Из этого соотношения выразим напряжение смещения : E = U0 + Um cosθ ; E = 3,075 + 1,53 cosθ ; Амплитуды гармоник рассчитываем по формуле: Ik=|SUmγk(θ)| 2,03|γk(θ)|
График зависимости амплитуд гармоник токов Ik от напряжения смещения E:  I,мА I,мА 2 2      1,5 1,5 1 1  0,5 0,5                1 2 3 4 5 E, В Расчет амплитуд гармоник методом пяти ординат. По заданной ВАХ определяем токи для пяти значений напряжения смещения: Е, Е+ Um , Е- Um , Е+ Um/2, Е- Um/2. Напряжение Е выбираем в пределах от 1,55 В до 4,65 В (6 разных значений). Для каждого значения смещения определяем амплитуды гармоник. Пусть E=2 B, Um=1,53 В. Е=2 В, i0=1.4 мА ; Е=3.53 В, imax=0 мА ; Е=0.47 В, imin=3.46 мА ; Е=2.765 В, i1=0.4 мА ; Е=1.235 В, i2=2.44 мА. I0= (imax + imin +2i1 +2i2 )/6, I0=1.5 мА; I1=(imax - imin + i1 -i2 )/3, |I1|=1.8 мА; I2=(imax + imin -2i0 )/4, |I2|=0.4 мА; I3=(imax - imin - 2i1 +2i2 )/6, |I3|=0.1 мА; Пусть E=3 B, Um=1,53 В. Е=3 В, i0=0.99 мА ; Е=4.53В, imax=0 мА ; Е=1.47 В, imin=2.13 мА ; Е=3.765 В, i1=0 мА ; Е=2.235В, i2=1.1 мА. I0= (imax + imin +2i1 +2i2 )/6, I0=0.72 мА; I1=(imax - imin + i1 -i2 )/3, |I1|=1.07 мА; I2=(imax + imin -2i0 )/4, |I2|=0.5 мА; I3=(imax - imin - 2i1 +2i2 )/6, |I3|=0.01 мА; Пусть E=4 B, Um=1,53 В. Е=4 В, i0=0мА ; Е=5.53В, imax=0 мА ; Е=2.47 В, imin=0.8 мА ; Е=4.765В, i1=0 мА ; Е=3.235В, i2=0 мА. I0= (imax + imin +2i1 +2i2 )/6, I0=0.13 мА; I1=(imax - imin + i1 -i2 )/3, |I1|=0.27 мА; I2=(imax + imin -2i0 )/4, |I2|=0.2 мА; I3=(imax - imin - 2i1 +2i2 )/6, |I3|=0.13 мА;  I,мА I,мА     2 2     1,5 1,5     1 1 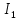           0,5 0,5 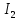             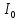 1 2 3 4 E, В  |
