“ Цифровая модуляция BPSK в системах мобильной связи при наличии помех и замираний в канале связи. Лабораторная 3. Лабораторная работа 3 " Цифровая модуляция bpsk в системах мобильной связи при наличии помех и замираний в канале связи "
 Скачать 1.37 Mb. Скачать 1.37 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ БАЛТИЙСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ им. И. КАНТА Институт физико-математических наук и информационных технологий Лабораторная работа №3 “ Цифровая модуляция BPSK в системах мобильной связи при наличии помех и замираний в канале связи ” Выполнили: Студенты 1 курса магистратуры Направления «ИКТиСС» профиль подготовки «МСиСС» Гладких Дмитрий Сергеевич Бахтияров Андрей Наилевич Проверил: Молчанов Сергей Васильевич Калининград 2020 Цель работы: изучение имитационной модели системы цифровой связи, анализ ее помехоустойчивости; приобретение навыков создания подсистем и их маскирования . Задание на лабораторную работу : 1. Создать с использованием среды MATLAB имитационные модели. 2. Построить графические зависимости для BER исследуемых моделей и проанализировать их. 3. С использованием программ Matlab (приложение 1, 2) выполнить расчеты по своему варианту для релеевского канала. 1. Исследование помехоустойчивость модуляции BPSK при оптимальном линейном сложении сигналов и оптимальном автовыборе. 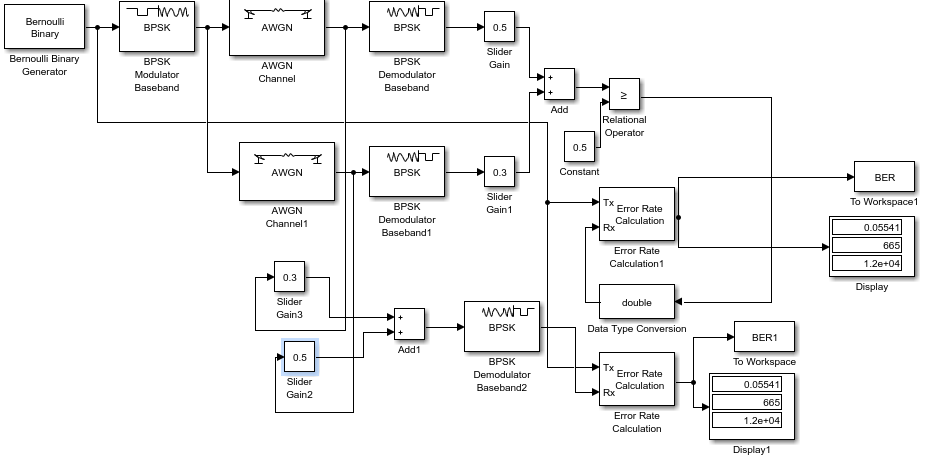  Таблица 1 Рис.1 - Имитационная модель оптимального линейного сложения сигналов и оптимального автовыбора.
 Таблица 2
 Таблица 4
 Рис.2- отношение Error Rate = f(SNR) при Eb/No=1 на первой ветви 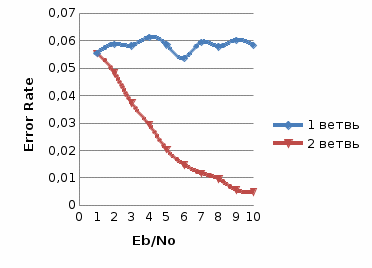  Рис.3- отношение Error Rate = f(SNR) при Eb/No=3 на первой ветви 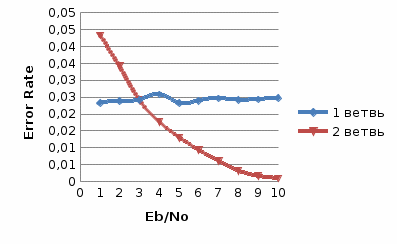  Рис.4- отношение Error Rate = f(SNR) при Eb/No=6 на первой ветви 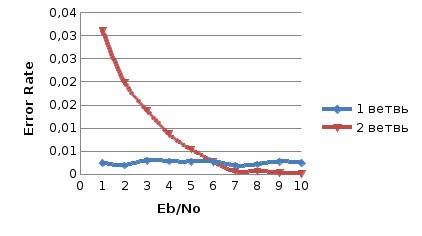  Рис.5- отношение Error Rate = f(SNR) при Eb/No=9 на первой ветви 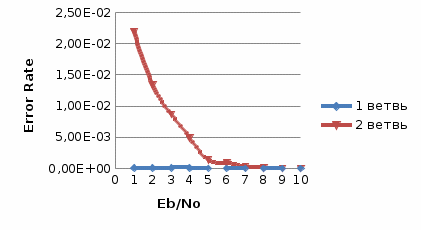 Выводы: Характеристики помехоустойчивости по сравнению с оптимальным сложением несколько меньше, так как помехи, содержащиеся в одних ветвях разнесения, суммируются с сигналами ветвей, которые помех практически не содержали. Сложение сигналов до демодуляции даёт меньший коэффициент помех - это обусловлено в основном пороговыми явлениями при демодуляции, когда при уменьшении входного ОСШ ниже некоторого порога после демодуляции выходное ОСШ начинает снижаться существенно быстрее, чем на входе демодулятора. При этом, поскольку во время додетекторного сложения ОСШ повышается, то пороговые явления наступают позднее, в чем и проявляется выигрыш. 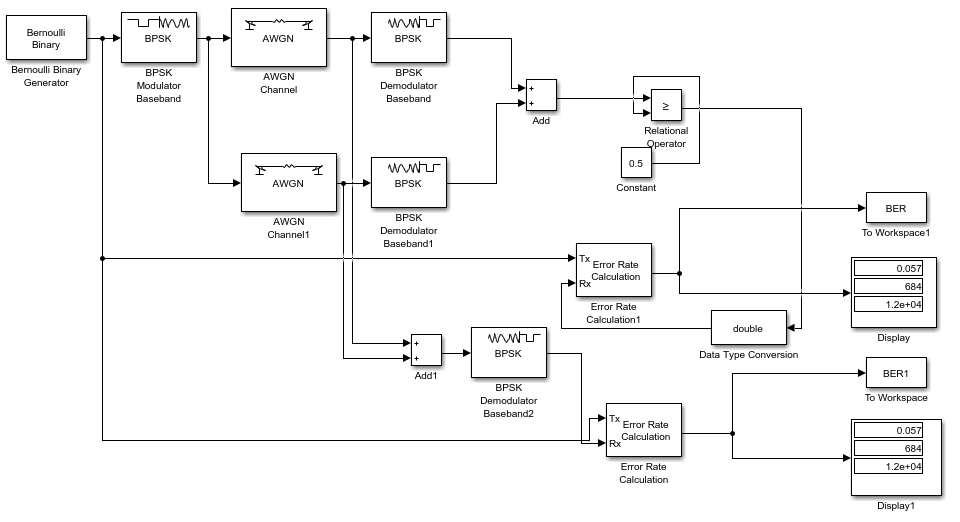  Таблица 5 Рис. 6. Имитационная модель линейного сложения сигналов
 Таблица 6
 Таблица 7
 Таблица 8  Рис.7- отношение Error Rate = f(SNR) при Eb/No=1 на первой ветви 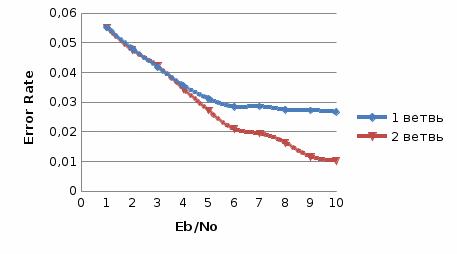  Рис.8- отношение Error Rate = f(SNR) при Eb/No=3 на первой ветви 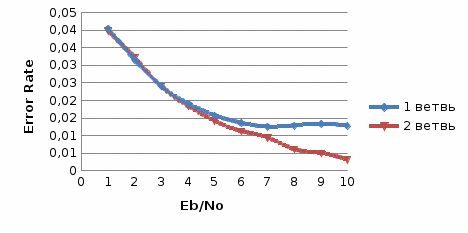  Рис.9- отношение Error Rate = f(SNR) при Eb/No=6 на первой ветви 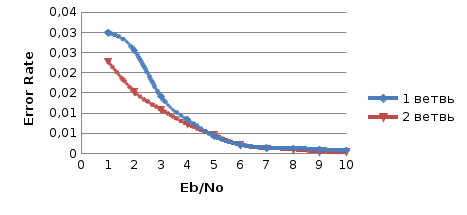 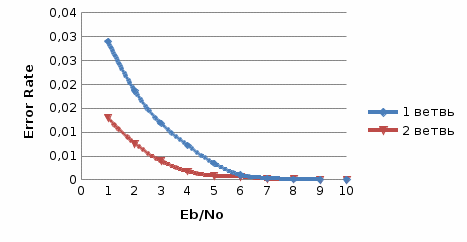  Рис.10- отношение Error Rate = f(SNR) при Eb/No=9 на первой ветви Выводы: наименьший выигрыш дает линейное сложение; единственным плюсом этого метода является простота реализации, не требующая анализа ветвей разнесения. 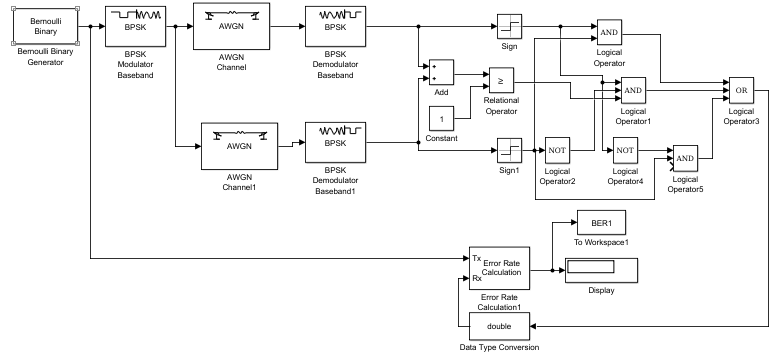 Рис.11. Имитационная модель комбинированной обработки цифровых сигналов при пространственном разнесении
 Таблица 9  Таблица 10
 Таблица 11
 Таблица 12
 Рис.12- отношение Error Rate = f(SNR) при Eb/No=1 на первой ветви 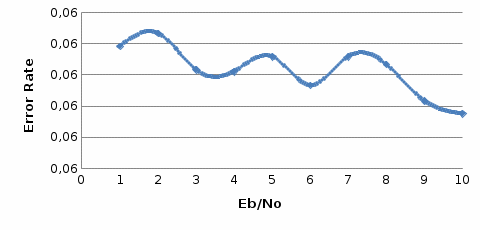  Рис.13- отношение Error Rate = f(SNR) при Eb/No=3 на первой ветви 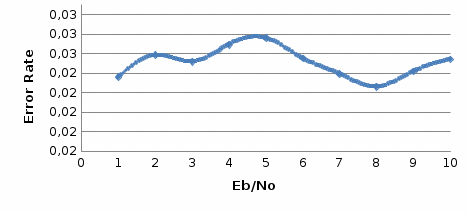  Рис.14- отношение Error Rate = f(SNR) при Eb/No=6 на первой ветви 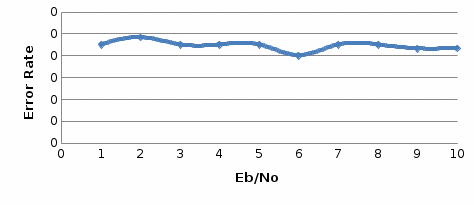 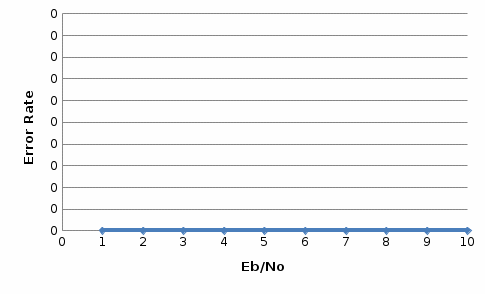  Рис.15- отношение Error Rate = f(SNR) при Eb/No=9 на первой ветви Выводы: применение комбинированного метода позволяет достигнуть похожих значений с оптимальным методом сложения, при этом используется более простая в реализации схема. Исследование помехоустойчивости модуляции BPSK 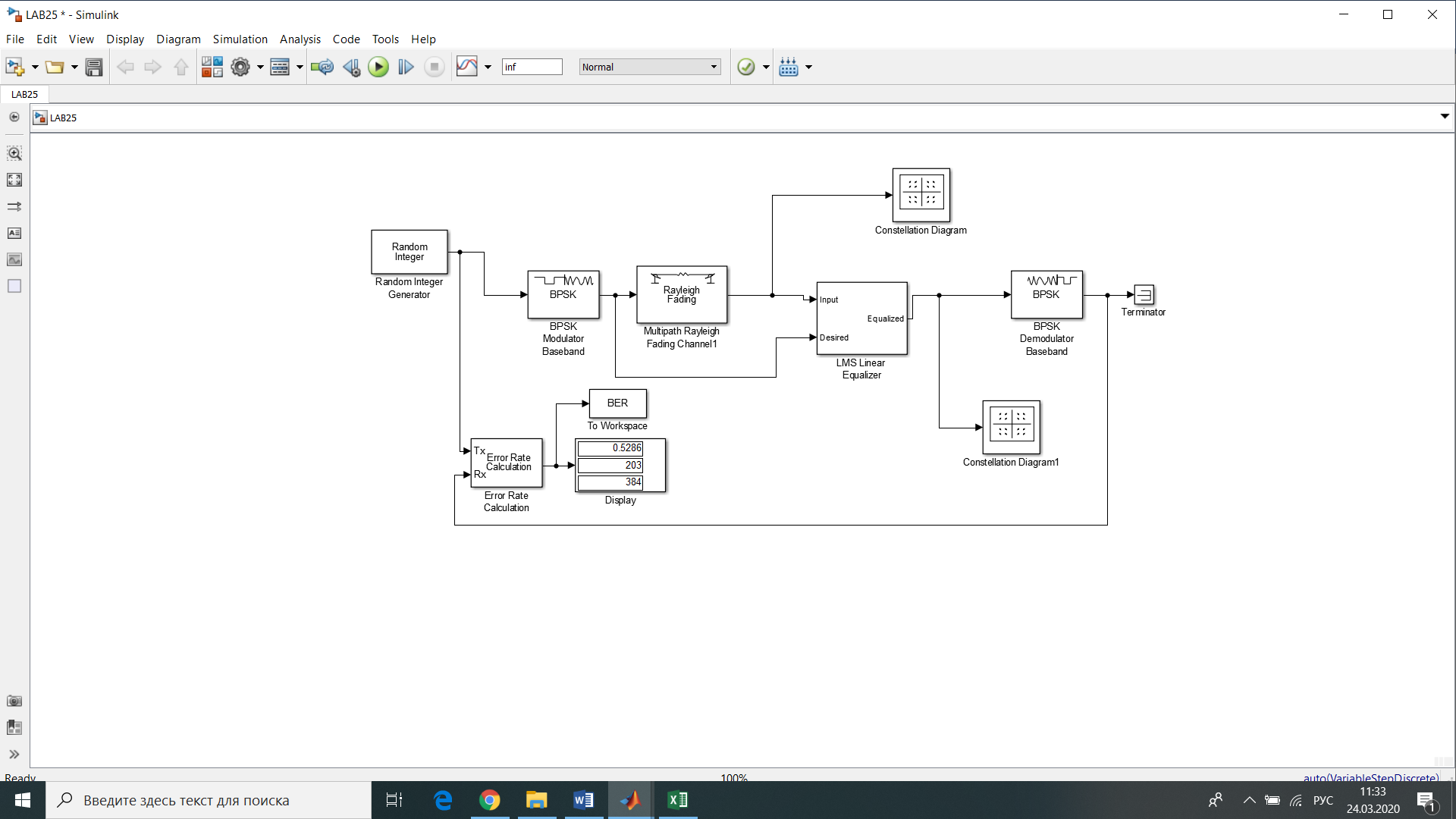 Рис. 16. Имитационная модель многолучевого канала. Рис. 17. Констелляционные диаграммы сигнала до (слева) и после (справа) эквалайзера импульсная характеристика сигнала на выходе демодулятора для разного числа лучей N. Число лучей – 1 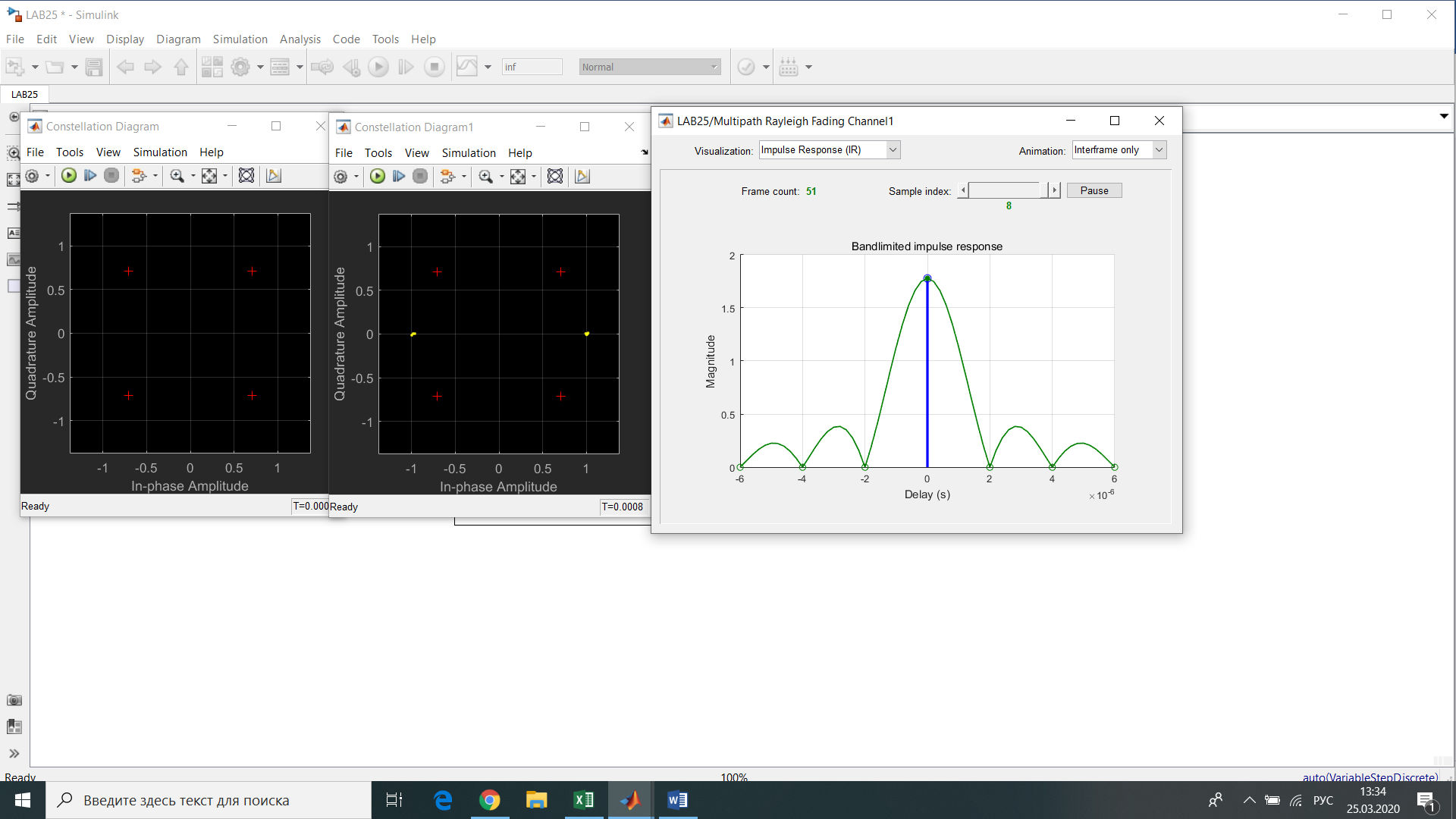 Число лучей – 2 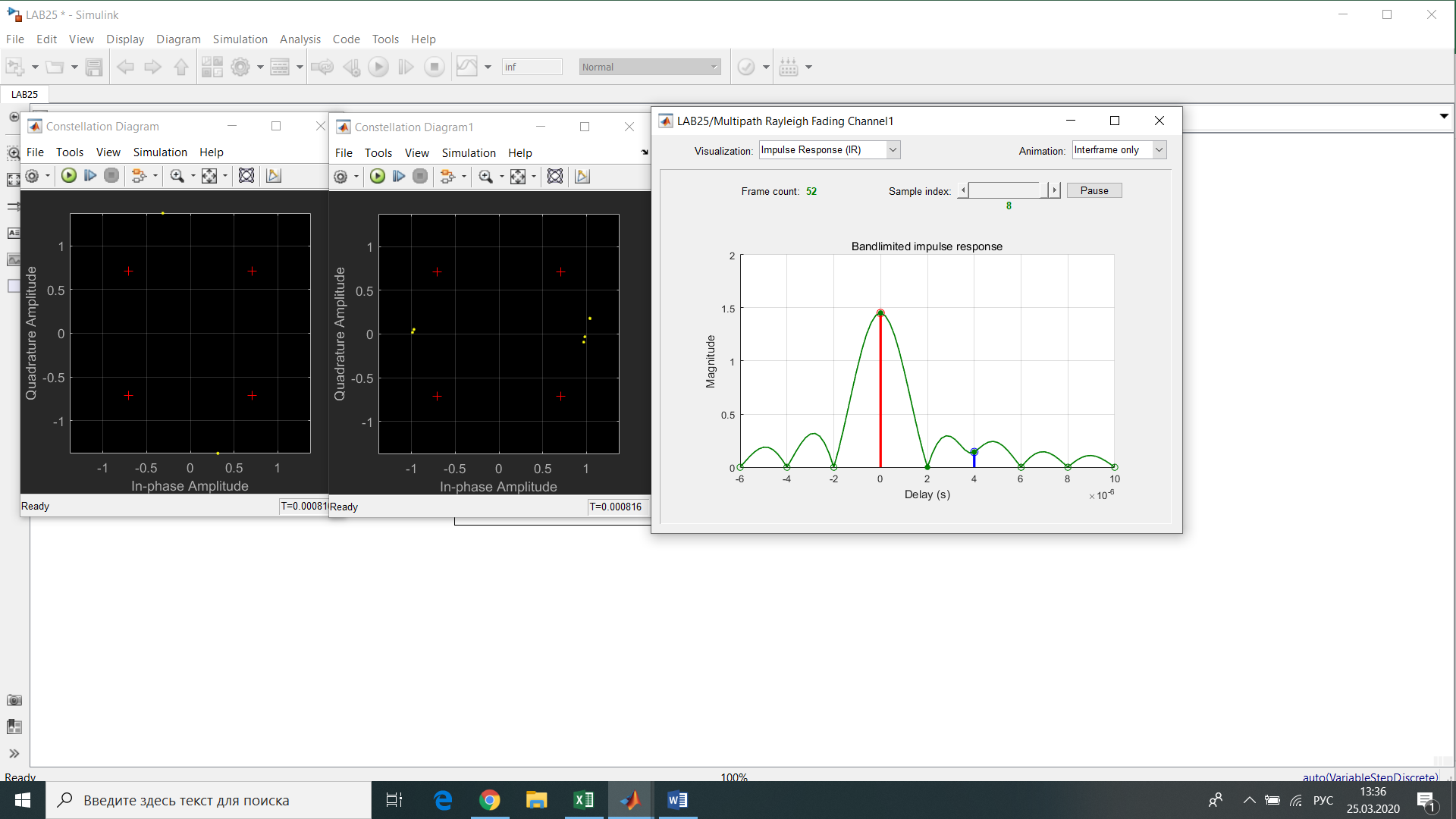 Число лучей – 3 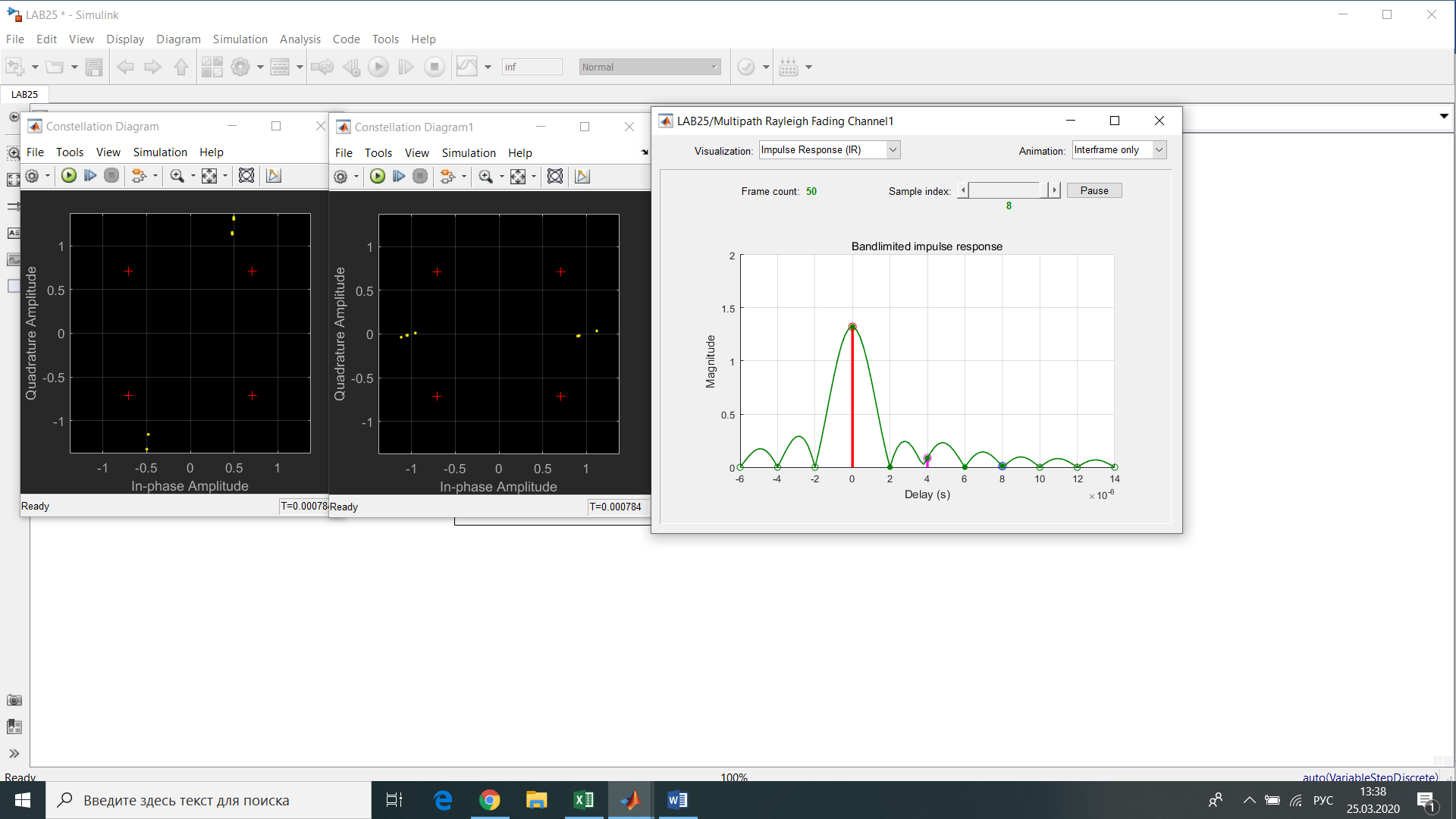 Число лучей – 4 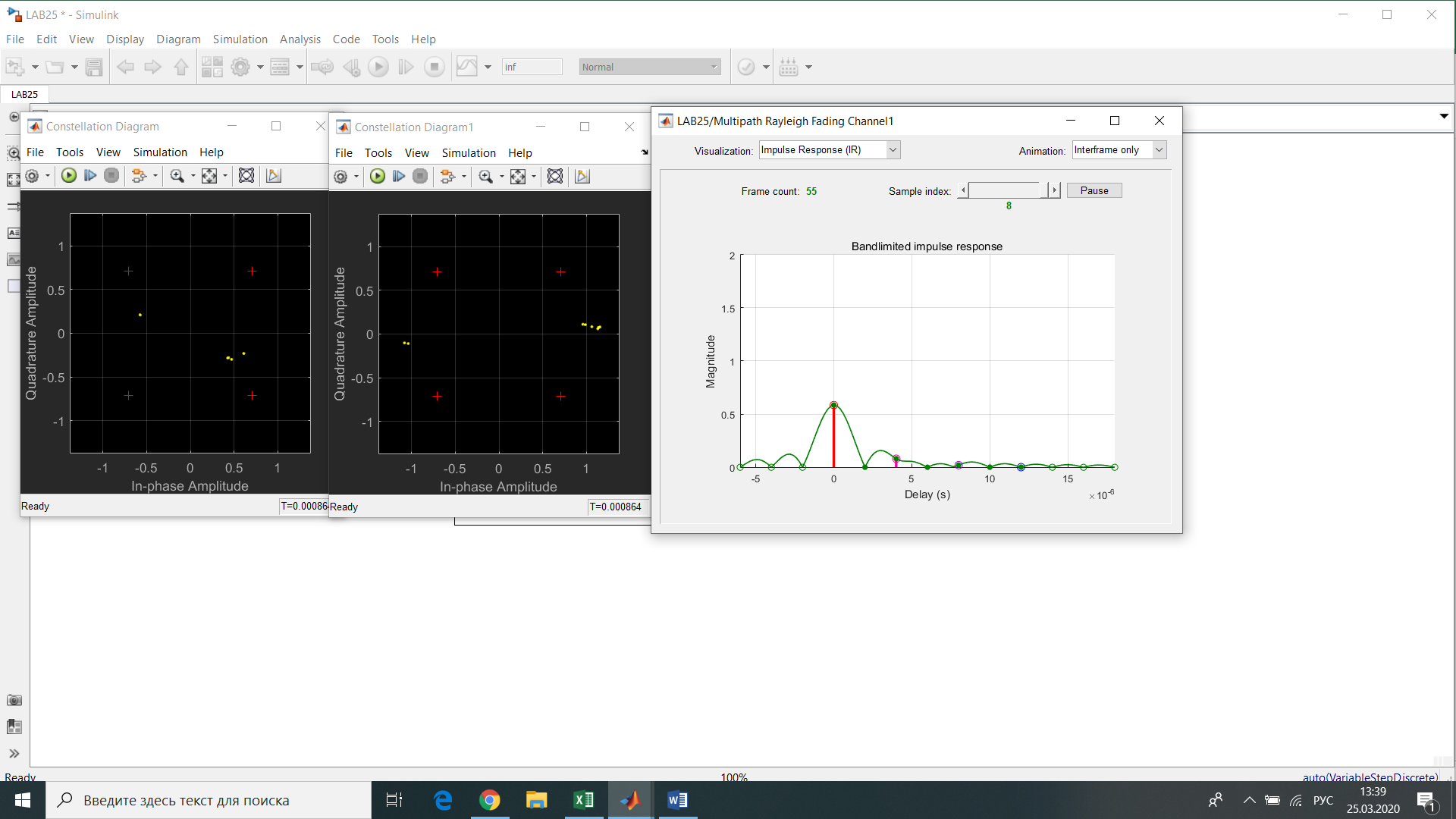 Число лучей – 5 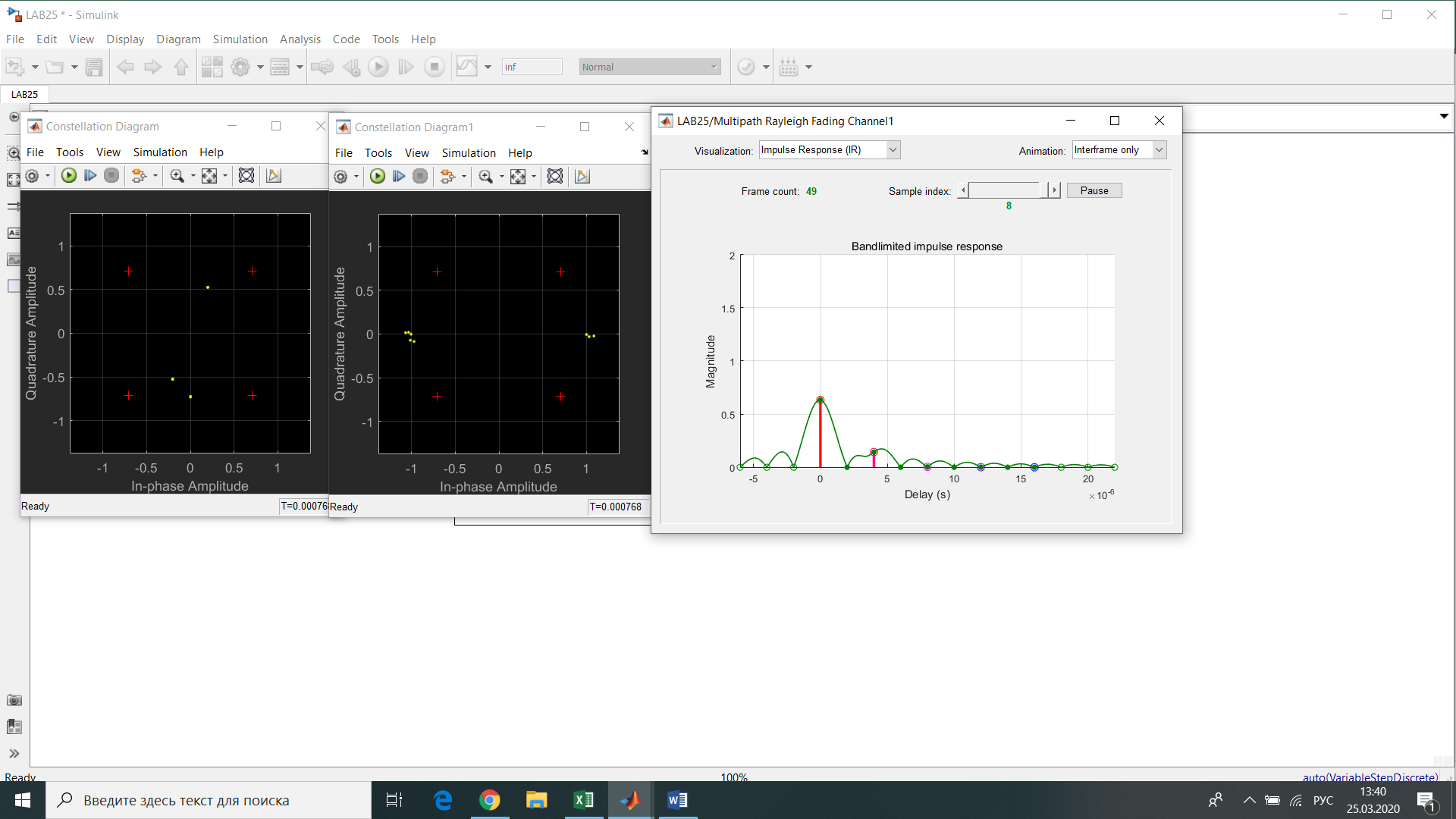 Число лучей – 6 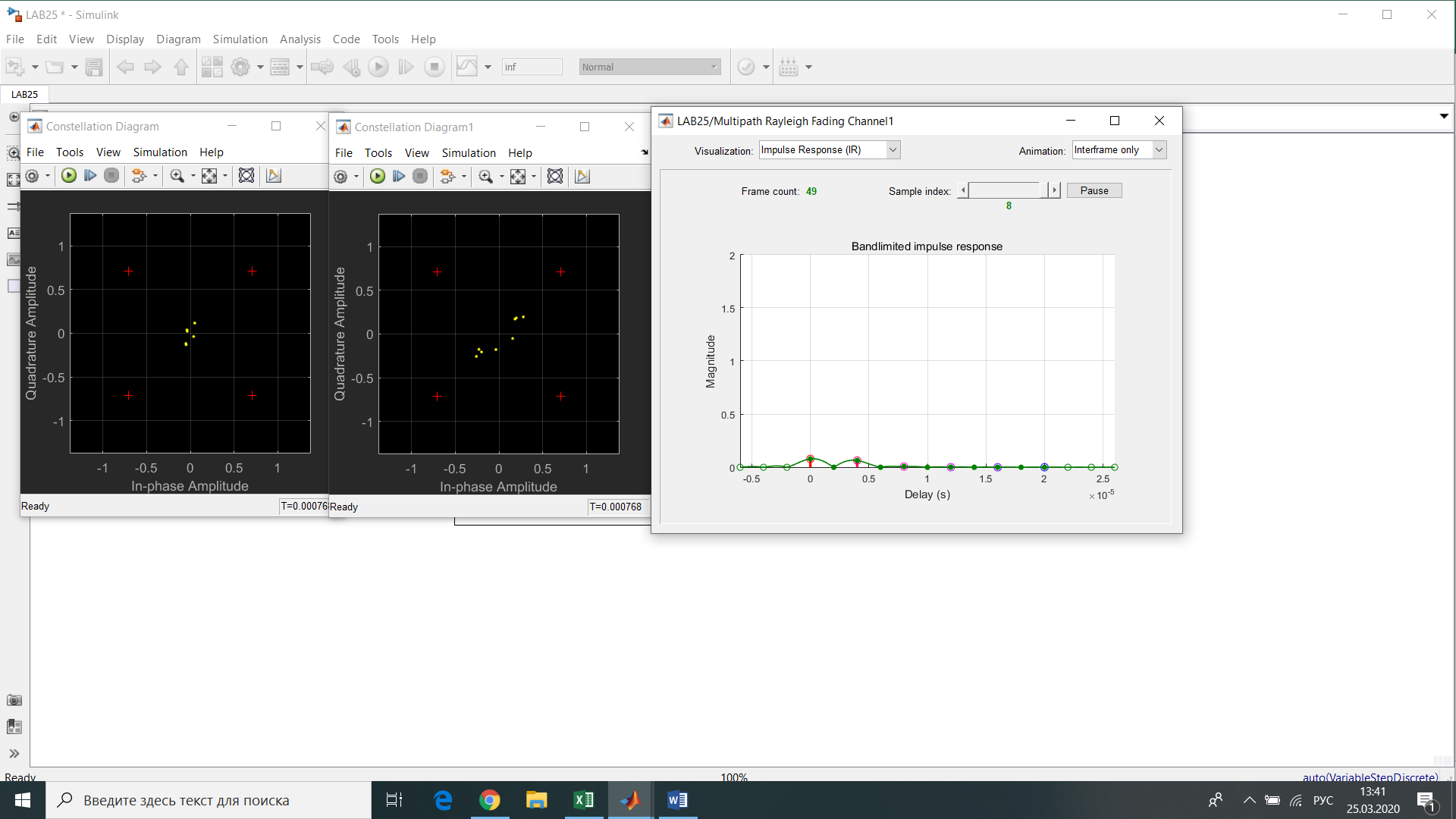 Таблица 13.
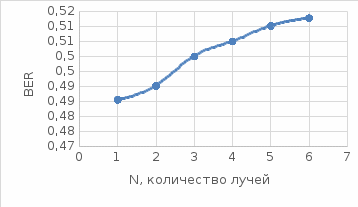 Рис. 18. График зависимости BER от количества лучей распространения сигнала N. Вывод: Из рисунков и графика видно, что качество детектируемого сигнала ухудшается с увеличением числа путей распространения сигнала. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
