Главная страница
Навигация по странице:

  • КРАТКАЯ ТЕОРИЯ

  • ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА

    		•

    Лабораторная работа эффект комптона. Лабораторная Эффект Комптона. Лабораторная работа 3 3 эффект комптона цель работы


    Скачать 135 Kb.
    НазваниеЛабораторная работа 3 3 эффект комптона цель работы
    АнкорЛабораторная работа эффект комптона
    Дата17.01.2021
    Размер135 Kb.
    Формат файлаdoc
    Имя файлаЛабораторная Эффект Комптона.doc
    ТипЛабораторная работа
    #168963

    ЛАБОРАТОРНАЯ РАБОТА № 3_3

    ЭФФЕКТ КОМПТОНА



    ЦЕЛЬ РАБОТЫ:

    1. Знакомство с моделями электромагнитного излучения и их использованием при анализе процесса рассеяния рентгеновского излучения на веществе.

    2. Экспериментальное подтверждение закономерностей эффекта Комптона.

    3. Экспериментальное определение комптоновской длины волны электрона.

    КРАТКАЯ ТЕОРИЯ:

    МОДЕЛИ электромагнитного излучения (ЭМИ):

    • луч – линия распространения ЭМИ (геометрическая оптика),

    • волна – гармоническая волна, имеющая амплитуду и определенную длину волны или частоту (волновая оптика),

    Характеристики всех моделей связаны друг с другом.
    ЭФФЕКТОМ КОМПТОНА называется появление рассеянного излучения с большей длиной волны при облучении вещества монохроматическим рентгеновским излучением.

    РЕНТГЕНОВСКИМ называется электромагнитное излучение, которое можно моделировать с помощью электромагнитной волны с длиной от 10–8 до 10–12 м или с помощью потока фотонов с энергией от 100 эВ до 106 эВ.

    Первая модель применяется для описания рентгеновского излучения, распространяющегося от источника до вещества. Оно представляется, как монохроматическая волна с длиной .

    В 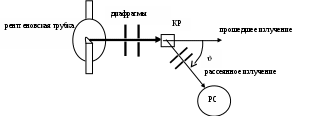олновая модель применяется и для описания рассеянного под углом  рентгеновского излучения, идущего от вещества (КР) до регистрирующего устройства (рентгеновского спектрометра РС).

    Рассмотрим процесс столкновения падающего рентгеновского фотона (энергия , импульс ) с покоящимся электроном вещества. Энергия электрона до столкновения равна его энергии покоя mc2, где m – масса покоя электрона. Импульс электрона равен 0.

    После столкновения электрон будет обладать импульсом и энергией, равной . Энергия фотона станет равной ′ , а импульс ′.

    Из закона сохранения импульса и энергии вытекают два равенства:
     + mc2 = ′ + и = + ′.

    Разделив первое равенство на второе, возведя в квадрат и проведя некоторые преобразования (см. учебник (3), с. 45), получим формулу Комптона:
     = ′ –  = C (1 – cos), где комптоновская длина волны C = . Для электрона C = 2,43 10–12 м.
    ИЗМЕРЕНИЯ

    1. Установим первое значение длины волны из табл. 2, соответствующее номеру вашей бригады.

    2. Установим первое значение регулятора угла приема рассеянного ЭМИ 60º1.

    3. По картине измеренных значений определите длину волны ′ рассеянного ЭМИ и запишите в первую строку таблицы 1.

    4. Изменяйте угол наблюдения с шагом 10º и записывайте измеренные значения ′ в соответствующие строки табл. 1.

    5. Заполнив все строки табл. 1, измените значение длины волны падающего ЭМИ в соответствии со следующим значением для вашей бригады из табл. 2. Повторите измерения длины волны рассеянного ЭМИ, заполняя сначала табл. 3, а затем и табл. 4 (аналогичные табл. 1).
    ТАБЛИЦА 1.Результаты измерений

    Длина волны  = 4 пм



    Номер

    измер.
    ,

    град
    ′,

    пм
    1– cos



    Длина волны

    падающего ЭМИ, пм

    1
    60
    4,12
    0,50



    4
    6
    9

    2
    70
    4,13
    0,66












    3
    80
    4,20
    0,83












    4
    90
    4,24
    1,00












    5
    100
    4,29
    1,17












    6
    110
    4,33
    1,34












    7
    120
    4,36
    1,50












    8
    130
    4,40
    1,64












    9
    140
    4,43
    1,77












    10
    150
    4,45
    1,87












    11
    160
    4,47
    1,94


















    ТАБЛИЦА 2.Результаты измерений

    Длина волны  = 6 пм



    Номер

    измер.
    ,

    град
    ′,

    пм
    1– cos






    1
    60
    6,12
    0,50












    2
    70
    6,16
    0,66












    3
    80
    6,20
    0,83












    4
    90
    6,24
    1,00












    5
    100
    6,29
    1,17












    6
    110
    6,33
    1,34












    7
    120
    6,36
    1,50












    8
    130
    6,40
    1,64












    9
    140
    6,43
    1,77












    10
    150
    6,45
    1,87












    11
    160
    6,47
    1,94


















    ТАБЛИЦА 3.Результаты измерений

    Длина волны  = 9 пм



    Номер

    измер.
    ,

    град
    ′,

    пм
    1– cos






    1
    60
    9,12
    0,50












    2
    70
    9,16
    0,66












    3
    80
    9,20
    0,83












    4
    90
    9,24
    1,00












    5
    100
    9,29
    1,17












    6
    110
    9,33
    1,34












    7
    120
    9,36
    1,50












    8
    130
    9,40
    1,64












    9
    140
    9,43
    1,77












    10
    150
    9,45
    1,87












    11
    160
    9,47
    1,94














    Табл. 2 и 3 аналогичны табл. 1.
    ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:

    1. Вычислим и запишем в табл. 1, 2 и 3 величины 1 – cos.

    2. Постройте график зависимости изменения длины волны ( = ′ – ) от разности (1 – cos ) для каждой серии измерений.


    Поскольку  = ′ –  есть одно и то же число для каждого измерения, то и график у них один.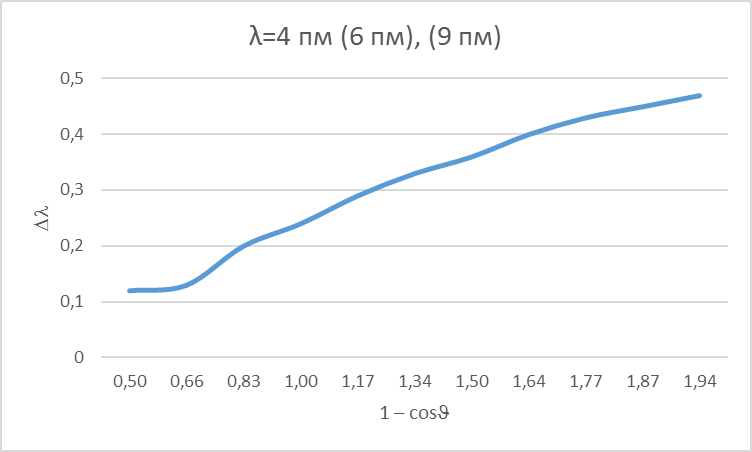



    1. Определим по наклону графика значение комптоновской длины волны электрона

    .




    1. Запишите ответ и проанализируйте ответ и графики.


    В результате измерений получили  = 2,43 10–12 м. Поскольку для электрона C = 2,43 10–12 м, то делаем вывод о правильности измерений.

    написать администратору сайта