какая то лаба. ЛБ3 Нургалиев Р.М. Лабораторная работа 3 (ат02) Решение систем линейных алгебраических уравнений методом прогонки студент Нургалиев Р. М
 Скачать 203.11 Kb. Скачать 203.11 Kb.
|
|
Лабораторная работа №3 (АТ-02) Решение систем линейных алгебраических уравнений методом прогонки Выполнил: студент Нургалиев Р.М. Преподаватель: Круглов В.Н. Введение В данной лабораторной работе требуется решить систему алгебраических уравнений методом прогонки. 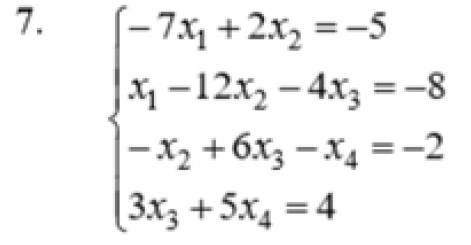 Рисунок 1. Пример Программа была написана на языке Python. В качестве IDE был использован Visual Studio Code Решение Прямой ход Прежде всего нам необходимо найти прогоночные коэффициенты. Они находятся по формулам 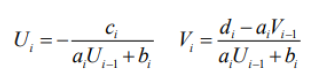 Рисунок 2.Формула коэффициентов Интерпретируем на язык программирования, получим функцию. 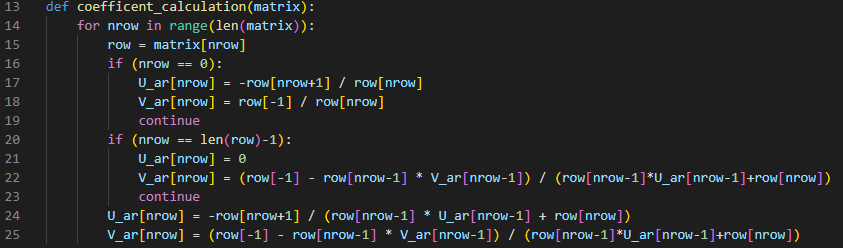 Рисунок 3. Находим коэффициенты прогонки Функция принимает на вход матрицу, в последней колонке свободные члены. 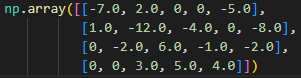 Рисунок 4. Исходная матрица Поскольку программа самостоятельно не может найти коэффициенты выходящие за границы массива, вносим 2 условия для первых двух и последних коэффициентов. Получаем коэффициенты(сверху Ui снизу Vi) [ 0.28571429 -0.34146341 0.14963504 -0.73409243] - Ui [ 0.71428571 0.74390244 -0.07664234 0.77628935] - Vi Обратный ход Теперь, зная коэффициенты мы можем найти все нужные x. Используем формулу 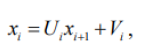 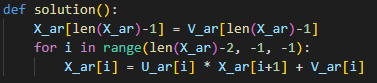 Рисунок 5. Формула нахождения x и ее интерпретация Получаем наши ответы [0.92297388 0.73040857 0.03951775 0.77628935] Вычисляем невязки В последнюю очередь необходимо найти невязки по формуле Рисунок 6. Формула нахождения невязок 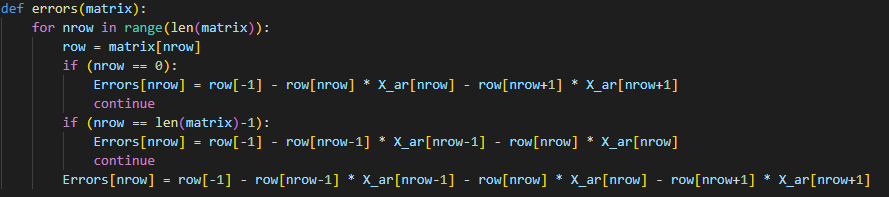 Рисунок 7. Функция нахождения невязок Получаем ответ: [-6.66133815e-16 8.32667268e-16 1.11022302e-16 0.00000000e+00] Принимаем значения в -16 степени как несущественные, следовательно равны нулю. Проверка Проверка была выполнена с помощью онлайн калькулятора (https://matrixcalc.org/ru/slu.html). Матрица была решена методом Гаусса и ответ не сайте совпадает с решением нашей программы. 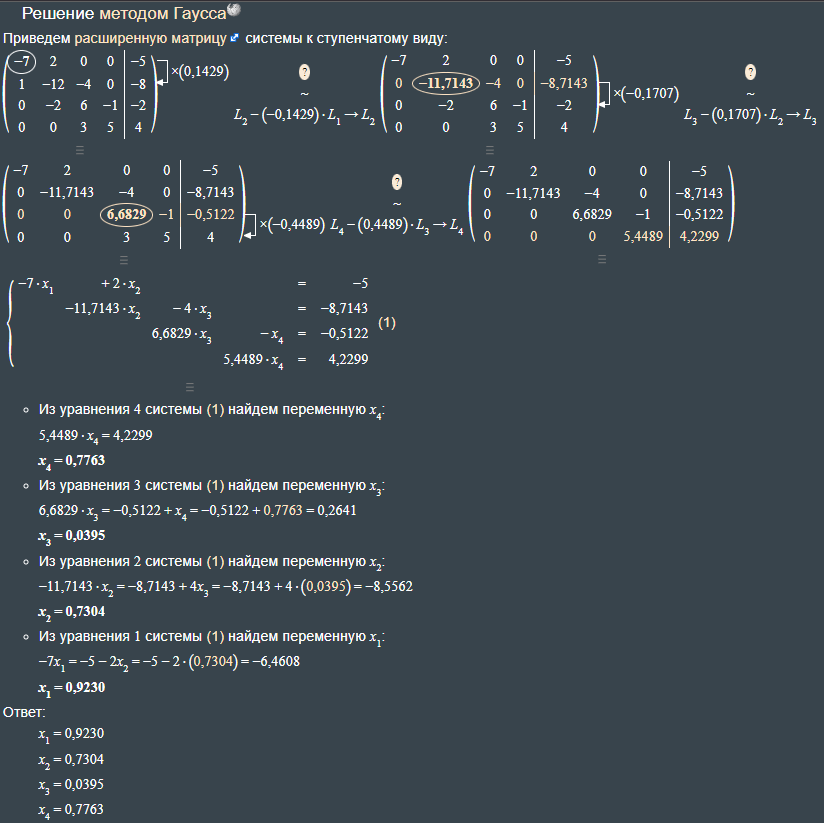 Вывод В ходе данной лабораторной работы, мы решили систему линейных уравнений методом прогонки и получили такие коэффициенты: [0.92297388 0.73040857 0.03951775 0.77628935] Проверили наше решение на онлайн ресурсе. Ответы совпали. |
