Отчет по лабораторной работе 3-4 экономика ХОДОС. Отчет по лабораторной 3-4, Колесникова А.К.. Лабораторная работа 3 моделирование равновесия потребителя в рамках ординалистского подхода в ms excel
 Скачать 136.35 Kb. Скачать 136.35 Kb.
|
|
Лабораторная работа 3-4. МОДЕЛИРОВАНИЕ РАВНОВЕСИЯ ПОТРЕБИТЕЛЯ В РАМКАХ ОРДИНАЛИСТСКОГО ПОДХОДА В MS EXCEL Цель работы: Изучить сущность кривых безразличия и линий бюджетного ограничения. Освоить построение кривых безразличия и линий бюджетного ограничения Microsoft Excel. Освоить построение кривой «доход-потребление» Microsoft Excel. Основные теоретические положения Кривая безразличия – линия, объединяющая ряд наборов, одинаково предпочтительных для потребителей. Бюджетное ограничение – ряд всех возможных наборов, доступных при данных ценах и доходах. Кривая «доход-потребление». Точки пересечения кривых безразличия с бюджетными ограничениями (Е1 , Е2 , …, Еn) показывают изменения положения равновесия потребителя при росте дохода или снижении цен. Соединив эти точки, получим кривую, названную Дж. Хиксом "доход — потребление". В экономической литературе она также получила название кривой уровня жизни. Кривая «доход-потребление» показывает, как при фиксированных ценах меняется потребление индивида по мере роста его бюджета. Если кривая "доход — потребление" выходит из начала координат под углом 45°, это значит, что с ростом дохода потребитель в одинаковой степени (пропорции) увеличивает потребление и блага X, и блага Y. Для большинства благ линия «доход - потребление» имеет положительный наклон (рис. а): с ростом дохода увеличивается потребление обоих благ (Х и У). Но по отношению к некоторым благам индивид имеет карту безразличия со сдвинутыми к одной из осей координат кривыми безразличия. В этом случае линия «доход - потребление» может иметь отрицательный наклон (рис. б): по мере роста дохода индивид сокращает потребление одного из благ. Такое благо условно называют «некачественным» (inferior good). 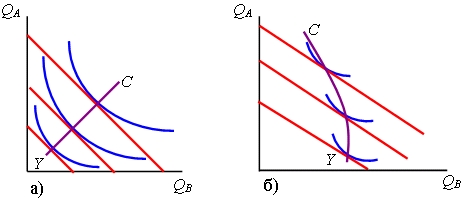 Практическая часть Доход потребителя составляет I руб. Он максимизирует полезность, покупая некоторые количества благ X и Y по рыночным ценам PX руб./шт. и PY руб./шт., соответственно. Функция полезности потребителя имеет вид TU (X,Y)=AXαYβ (функция Кобба-Дугласа). Значения параметров функции полезности Кобба-Дугласа TU (X,Y)=AXαYβ для двух товаров, доход, цены товаров X и Y. Численные значения параметров задачи:
Преобразование функции Кобба-Дугласа позволило нам определить: X = (α : (α+ β)) * (I: PX) Y = (β : (α+ β)) * (I: Pу) Для нашей задачи оптимальные количества благ X и Y равны: X =1,49 ед. Y = 5,16 ед. Полезность данного набора определим. Подставив данные в функцию полезности TU (X,Y) = 54,47 (ют.) TU (X,Y) = 9*1,490,4*5,161,0= 54,47 (ют.) Для решения задачи графическим способом необходимо построить карту кривых безразличия и бюджетное ограничение в одной системе координат. Для того чтобы построить кривую безразличия, соответствующую уровню полезности U0, надо выразить из функции полезности Y через X и TU и придать TU значение U0: TU (X,Y) = 9*X0,4*Y1,0 Y =U0/9*X0,4 Построим кривые безразличия, для которых значение общей полезности потребления двух благ равняется 54,47 Обозначим их как U1, U2, U3, U4 и U5. Для этого создадим таблицу в программе Ecxel и рассчитаем значения Y для разных значений полезности.
Используя функцию «Вставка» построим точечную диаграмму (карту кривых безразличия).   X Y 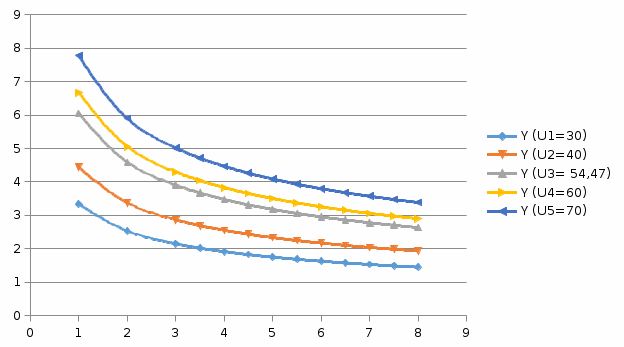 Рисунок 1 – График кривых безразличия Для построения бюджетного ограничения найдем две крайние точки: на оси Х – I/Px; на оси Y – I/Py
Используя функцию «Выбор источника данных» добавим расчетные данные для отображения бюджетной линии на карте кривых безразличия. 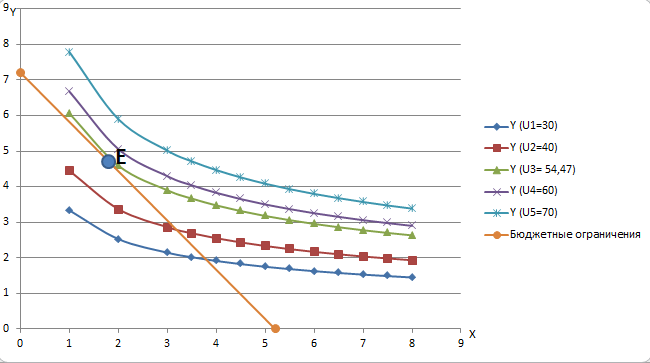 Рисунок 2 – Бюджетная линия на карте безразличия Точка касания E кривой безразличия с бюджетным ограничением представляет собой оптимальный потребительский набор, максимизирующий полезность потребителя. Построение кривой «доход-потребление» Кривая «доход-потребление» - кривая, показывающая товарные наборы, на которые предъявляется спрос при постоянных ценах на товары и различных уровнях дохода. Геометрически это линия, проходящая через оптимальные наборы благ при различных вариантах бюджетных ограничений. Рассчитаем оптимальные значения X и Y при разном доходе.
Используя функцию «Выбор источника данных» добавим расчетные данные для отображения линии «доход-потребление» на карте кривых безразличия. 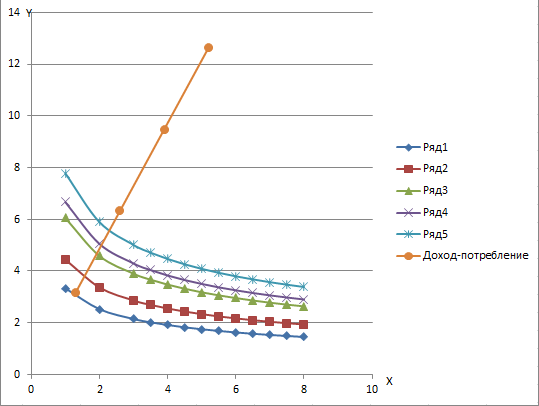 Рисунок 3 – График дохода и потребления Выводы по работе Мы определили набор благ, при котором потребитель максимизирует свою полезность. Рассчитанные данные: TU (X,Y) = 54,47 (ют.), X =1,49 ед. Y = 5,16 ед. Также по этим данным, которые предоставлены выше, можно увидеть как работает ординалистский подход, а точнее, что предпочтения индивидуума не могут измеряться количественно, а только сравниваться, то есть одна альтернатива хуже или лучше другой. |
