Лаба. Лабораторная работа 3 Нарушения допущений классической модели линейной регрессии Задания

• Название: Лабораторная работа 3 Нарушения допущений классической модели линейной регрессии Задания
• Дата: 04.05.2022
• Размер: 0.94 Mb.
• Имя файла: Laboratornaya_rabota_3.doc
• Тип: Лабораторная работа; #511166

8.4 Лабораторная работа № 3
Нарушения допущений классической модели линейной регрессии
Задания

1 Проведите графический анализ остатков. Проверьте остатки на гетероскедастичность с помощью:

- графического анализа,

- теста Голдфелда-Квандта,

- теста ранговой корреляции Спирмена,

- теста Уайта (White test).

2 Если будет обнаружена гетероскедастичность остатков, примените для исходных данных ОМНК, предполагая, что .

3 Проверить остатки на наличие автокорреляции первого порядка, используя метод рядов, критерий Дарбина – Уотсона и Q- статистику Льюинга – Бокса. Если гипотеза об отсутствии автокорреляции первого порядка не будет отвергнута, то применить ОМНК для оценивания параметров уравнения регрессии.
Реализация типовых заданий
1 Провести графический анализ остатков
В лабораторной работе № 1 выявили, что на чистый доход (y) предприятий оказывают влияния такие факторы, как использованный капитал (x₂) и численность служащих (x₃).

Для нахождения остатков можно воспользоваться инструментом анализа данных Регрессия. Порядок действий следующий:

а) в главном меню выберите Сервис/Анализ данных/Регрессия. Щелкните по кнопке ОК;

б) заполните диалоговое окно ввода данных и параметров ввода как показано на рисунке 8.8:

Входной интервал Y – диапазон, содержащий данные результативного признака;

Входной интервал Х – диапазон, содержащий данные всех пяти факторов;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист - можно задать произвольное имя нового листа;

Остаток - флажок, указывает вывод остатков 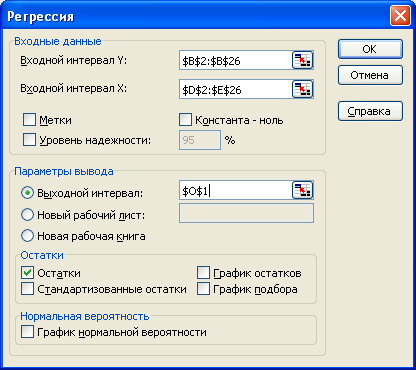и теоретические значения результативного признака.


Рисунок 8.8 – Регрессия с остатками
Результаты регрессионного и корреляционного анализа, а также вспомогательные характеристики представлены на рисунке 8.9.

Рисунок 8.4.2 – Вывод остатков

Проверим остатки полученного уравнения регрессии на гетероскедастичность.
Графический анализ остатков
Построим графики остатков для каждого уравнения (рисунок 8.10 и 8.11)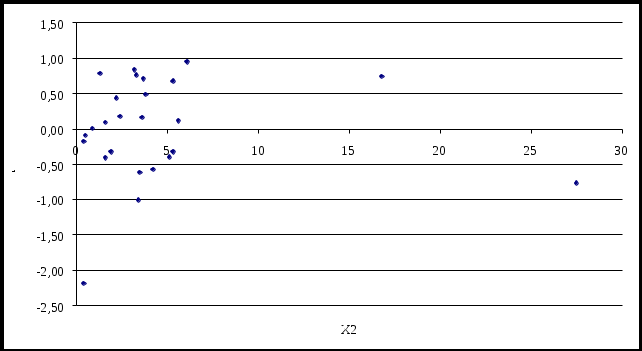



Рисунок 8.10 – График остатков для фактора х₂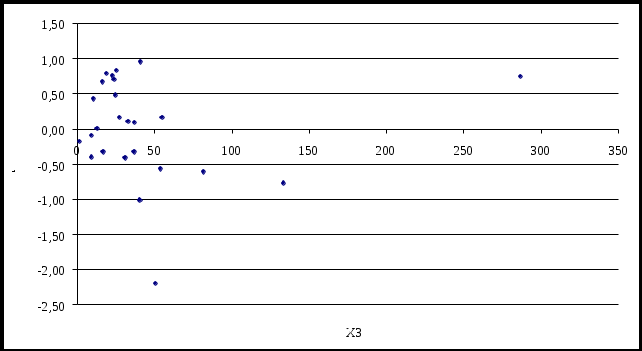



Рисунок 8.11 – График остатков для фактора х₃
Как видно на рисунке отклонения не лежат внутри полуполосы постоянной ширины, это говорит, о зависимости дисперсионных остатков от величины х₃ и о их непостоянстве, т.е. о наличии гетероскедастичности.
Тест Голфелда-Квандта
Выдвигаются гипотезы:

Н_о: - гомоскедастичность

Н₁: - гетероскедастичность

Порядок проведения теста следующий:

1 Все n наблюдений упорядочиваются по величине X₂ и X₃ (таблица 8.12 и 8.13).
Таблица 8.12 – Упорядоченные значения по фактору х₂

№ предприятия
1	2	3
1	2	0,4
2	0,7	0,4
3	2,2	0,5
4	2,4	0,9
5	3,3	1,3
6	2,9	1,6
7	2,3	1,6
8	2,5	1,9
9	2,9	2,2
10	2,9	2,4
11	3,6	3,2
12	3,5	3,3
13	2	3,4
14	3	3,5
15	3,4	3,6
16	3,5	3,7
17	3,3	3,8
18	2,7	4,2
19	2,3	5,1
20	3,5	5,3
21	2,5	5,3
22	3,2	5,6
23	4,2	6,1
24	8,5	16,8
25	5,7	27,5

2 Исключим С центральных наблюдений, разобьем совокупность на две части: а) со значениями x ниже центральных; б) со значениями x выше центральных.

Пусть С=5, это наблюдения с порядковыми номерами 11-15.

3 Оцениваются отдельные регрессии для первой подвыборки (10 первых наблюдений) и для третьей подвыборки (10 последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям X верно, то дисперсия регрессии по первой подвыборке (сумма квадратов отклонений ) будет существенно меньше дисперсии регрессии по третьей подвыборке (суммы квадратов отклонений ).
Таблица 8.13 – Упорядоченные значения по фактору х₃

№ предприятия
1	2	3
1	1,6	2
2	8,9	2,2
3	9,2	2,3
4	10,3	2,9
5	12,9	2,4
6	16,4	3,5
7	16,5	2,5
8	19,3	3,3
9	22,8	3,5
10	23,8	3,5
11	24,9	3,3
12	25,2	3,6
13	27,2	2,9
14	31,1	2,3
15	32,9	3,2
16	36,9	2,5
17	37,2	2,9
18	40,4	2
19	40,8	4,2
20	50,4	0,7
21	53,8	2,7
22	54,6	3,4
23	81,5	3
24	133,5	5,7
25	286,5	8,5

4 По каждой части находим уравнение регрессии (рисунок 8.12)



Рисунок 8.12 – Вывод итогов для подвыборок для фактора х₂
5 Для сравнения соответствующих дисперсий строится следующая F-статистика:

,

.

При сделанных предположениях относительно случайных отклонений построенная F-статистика имеет распределение Фишера с числами степеней свободы v₁=v₂=(n-C-2m)/2.

6 Если , то гипотеза об отсутствии гетероскедастичности отклоняется ( - выбранный уровень значимости).

По проведенным расчетам мы получили, что следовательно в ряду остатков обнаружена гетероскедастичность.

Аналогично проводится анализ для фактора х₃.
Тест ранговой корреляции Спирмена
Выдвигаются гипотезы:

Н_о: (отсутствие гетероскедастичности);

Н₁: (наличие гетероскедастичности).
Значения х_i и абсолютные величины u_i ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:

,

где d_i - разность между рангами х_i и u_i, i = 1, 2, ..., n;

n - число наблюдений.

Рассчитаем теоретические значения 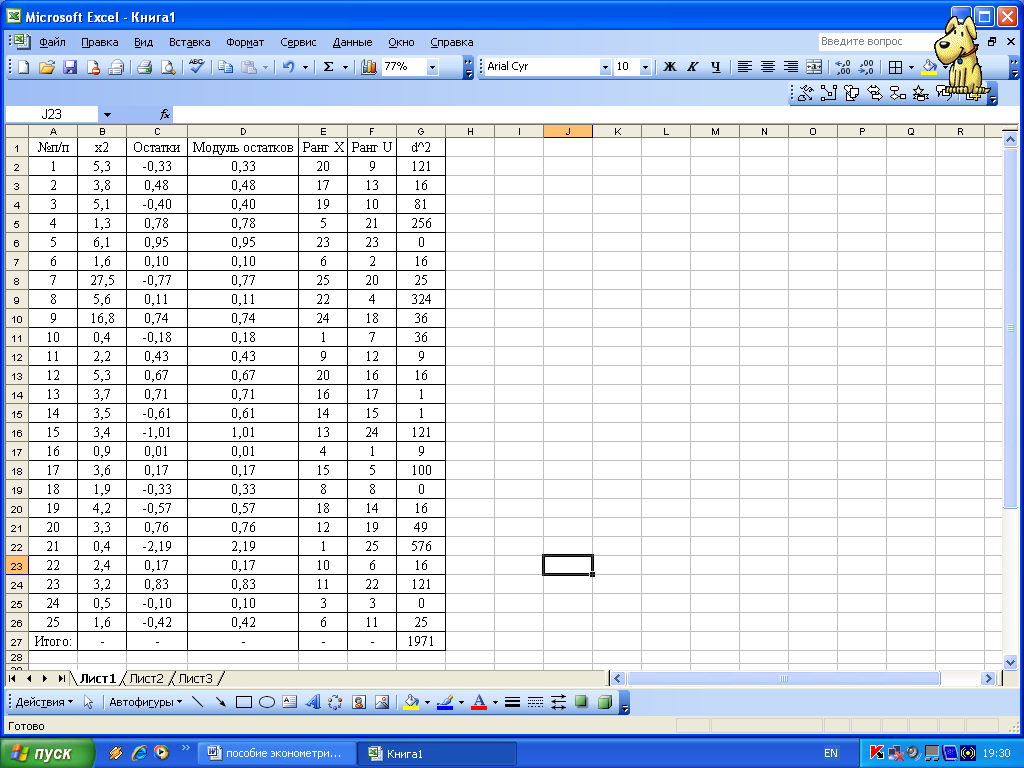по уравнению регрессии и найдем остатки. Ранжируем совокупность по возрастанию (рисунок 8.13).

Рисунок 8.13 – Расчетная таблица для проведения теста Спирмена
Тогда .

Если коэффициент корреляции для генеральной совокупности равен нулю, то статистика



имеет распределение Стьюдента с числом степеней свободы v=n-2. Следовательно, если наблюдаемое значение t-статистики превышает табличное, то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции , а следовательно, и об отсутствии гетероскедастичности.

В нашем примере статистика Стьюдента равна: .

Табличное значение статистики Стьюдента составит t_{(0,05; 23)}=2,0687.

Таким образом, мы получили, что расчетное значение меньше табличного, следовательно, гипотеза об отсутствии гетероскедастичности принимается на уровне значимости 5 %.

Аналогично проводится анализ для фактора х₃.
Тест Уайта(Whitetest).
Выдвигаются гипотезы:

Н_о: - уравнение статистически незначимо (гомоскедастичность);

Н₁: - уравнение статистически значимо (гетероскедастичность).
Тест Уайта позволяет оценить количественно зависимость дисперсии ошибок регрессии 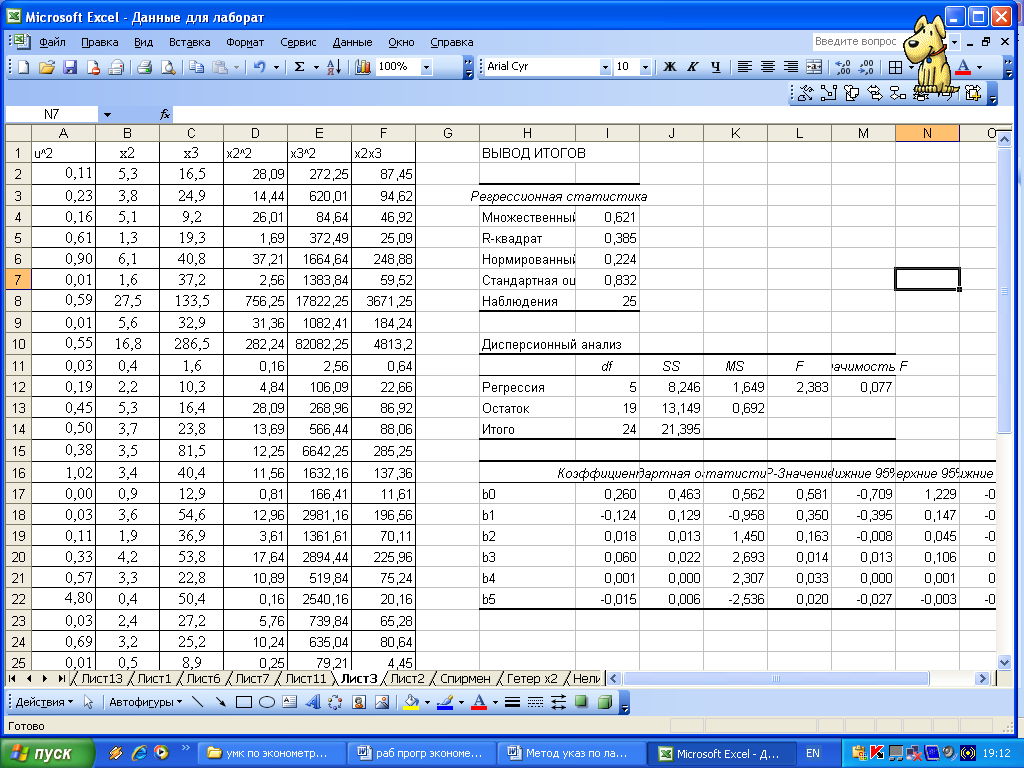от значений фактора x, используя квадратичную функцию:

,

где - нормально распределенная ошибка.


Рисунок 8.14 – Вывод итогов вспомогательной регрессии теста Уайта
Проводится этот тест следующим образом:

1) получаем регрессионные остаткиu_i;

2) оцениваем вспомогательную регрессию;

Гипотеза об отсутствии гетероскедастичности принимается в случае незначимости регрессии в целом.

3) в нашем примере вспомогательная регрессия принимает вид:

.

Уравнение статистически незначимо на уровне значимости . Следовательно, гипотеза об отсутствии гетероскедастичности принимается.
2 Если будет обнаружена гетероскедастичность остатков, примените для исходных данных ОМНК, предполагая, что .

По всем проведенным тестам можно сделать вывод о гомоскедастичности регрессионных остатков. В противном случае для устранения гетероскедастичности необходимо применить к исходным данным обобщенный метод наименьших квадратов в предположении, что .

Исходное уравнение преобразуем делением правой и левой частей на x₂: . К нему применим МНК. Полученное уравнение имеет вид: . Получены новые оценки параметров линейного уравнения, в котором смягчена гетероскедастичность.


Рисунок 8.15– Вывод итога ОМНК
3 Проверить остатки на наличие автокорреляции первого порядка, используя метод рядов, критерий Дарбина – Уотсона и Q- статистику Льюинга – Бокса. Если гипотеза об отсутствии автокорреляции первого порядка не будет отвергнута, то применить ОМНК для оценивания параметров уравнения регрессии.

Метод рядов

Последовательно определяются знаки остатков .

Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называется длиной ряда.

Пусть n — объем выборки;

n₁ — общее количество знаков «+» при n наблюдениях;

n₂ — общее количество знаков «-» при n наблюдениях;

k — количество рядов.

Если при достаточно большом количестве наблюдений (n₁>10, n₂>10) количество рядов k лежит в пределах от k₁ до k₂: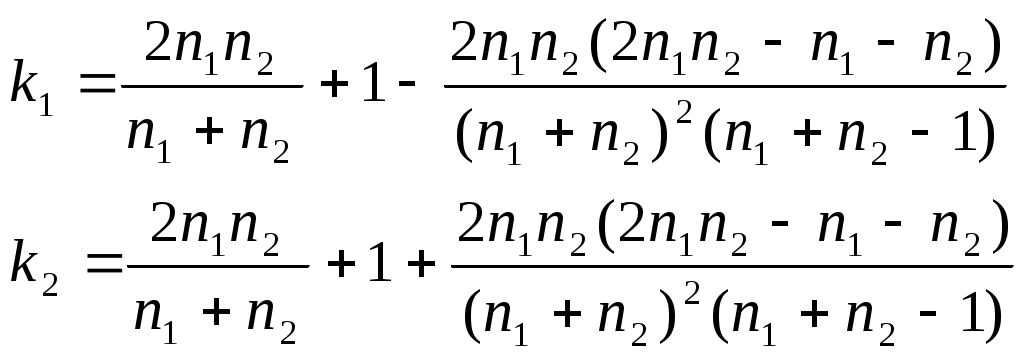
,
то гипотеза об отсутствии автокорреляции не отклоняется.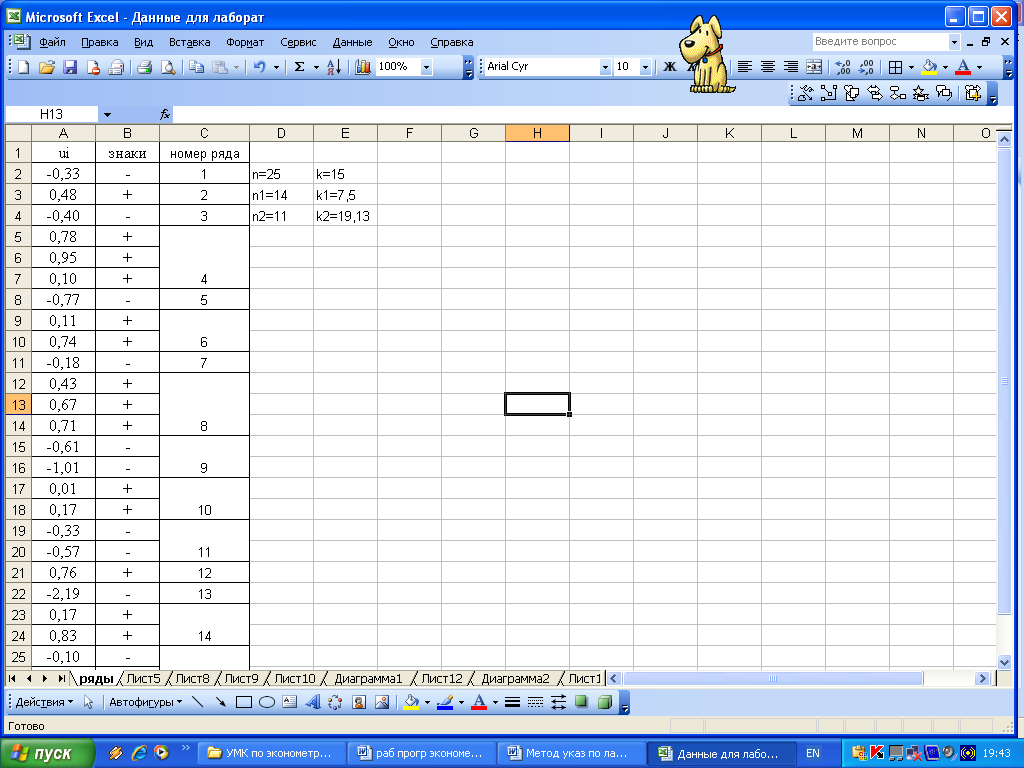


Рисунок 8.16 – Расчет характеристик метода рядов
Найдя знаки отклонений теоретических уровней от фактических, мы получили, что в анализируемой выборке содержится 15 рядов, т.е. k=15 (рисунок 8.16). Общее количество знаков «+» n₁=14, количество знаков «-» n₂=11.

Подставим найденные значения в формулу, получим, что k₁=7,5, k₂=19,13. Следовательно, гипотеза об отсутствии автокорреляции не отклоняется.
Критерий Дарбина – Уотсона

Для проверки автокорреляции первого порядка необходимо рассчитать критерий Дарбина—Уотсона. Он определяется так:

.

Выдвигается гипотеза Н₀ об отсутствии автокорреляции остатков. При сравнении расчетного значения статистики (DW<2) с d_l и d_u возможны следующие варианты.

1 Если DW< d_l , то гипотеза Н₀ отвергается.

2 Если DW > d_u, то гипотеза Н₀ не отвергается.

3 Если d_l< DW< d_u, то нельзя сделать определенного вывода по имеющимся исходным данным (зона неопределенности).

При DW > 2, то с табличными значениями сравнивается величина (4-DW).


Рисунок 8.17 – Расчет критерия Дарбина – Уотсона
В результате проведенных расчетов получено значение критерия Дарбина - Уотсона DW=2,2032 (рисунок 8.17). Так как оно больше 2, то с критическими значением сравниваем величину 4-DW=1,7967. Оно больше d_uследовательно мы не можем отвергнуть гипотезу Н₀ – в ряду остатков отсутствует автокорреляция первого порядка.
Q-тест Льюинга – Бокса
Использование данного теста предполагает использование Q- статистики, значение которой определяется по формуле:

,

где - выборочные значения автокорреляционной функции;

- величина лага;

n – число наблюдений.

Q- статистика имеет - распределение с степенями свободы. Если Q - статистика меньше табличного , то гипотеза об отсутствии автокорреляции принимается.

Рассчитаем для нашей задачи Q- статистику. Для этого необходимо определить коэффициенты автокорреляции. Максимальная величина лага не должна превышать ¼ числа наблюдений, т.е. в рассматриваемом примере . Следовательно нужно определить автокорреляции до шестого порядка. Для этого используем функцию Excel сервис–анализ данных – корреляция (рисунок 8.18).


Рисунок 8.18 – Расчет Q-статистики Льюинга - Бокса
Подставив полученное значение в формулу, получим:

.

Табличное значение .

Фактическое значение статистики меньше критического, следовательно, гипотеза принимается, т.е. в ряду остатков отсутствует автокорреляция.