Лабораторная работа3. Лабораторная работа 3 Оптимизация последовательности переналадок технологической линии Постановка задачи

• Название: Лабораторная работа 3 Оптимизация последовательности переналадок технологической линии Постановка задачи
• Дата: 21.02.2019
• Размер: 78.34 Kb.
• Имя файла: Лабораторная работа3.docx
• Тип: Лабораторная работа; #68534
• страница: 1 из 4

Лабораторная работа №3
Оптимизация последовательности переналадок технологической линии
Постановка задачи
Для обработки на технологичной линии поступило 7 партий заготовок. При переходе от обработки одной партии к следующей необходимо выполнить переналадку технологических линий, для обработки всех партий необходимо 6 таких переналадок. Задача состоит в определении такого порядка запуска партий заготовок на обработку, при котором суммарное время переналадок было бы минимальным

	1	2	3	4	5	6	7
1	M	11	10	17	6	8	9
2	9	M	14	15	7	8	9
3	7	9	M	5	8	4	5
4	6	10	7	M	5	8	6
5	15	12	6	9	M	7	7
6	7	14	7	8	7	M	6
7	9	11	7	8	10	5	M

()

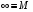Решение.

Возьмем в качестве произвольного маршрута:

X₀ = (1,2);(2,3);(3,4);(4,5);(5,6);(6,7);(7,1)

Тогда F(X₀) = 11 + 14 + 5 + 5 + 7 + 6 + 9 = 57

Для определения нижней границы множества воспользуемся операцией редукции или приведения матрицы по строкам, для чего необходимо в каждой строке матрицы D найти минимальный элемент.

d_i = min(j) d_ij

i j	1	2	3	4	5	6	7	di
1	M	11	10	17	6	8	9	6
2	9	M	14	15	7	8	9	7
3	7	9	M	5	8	4	5	4
4	6	10	7	M	5	8	6	5
5	15	12	6	9	M	7	7	6
6	7	14	7	8	7	M	6	6
7	9	11	7	8	10	5	M	5

Затем вычитаем d_i из элементов рассматриваемой строки. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.

i j	1	2	3	4	5	6	7
1	M	5	4	11	0	2	3
2	2	M	7	8	0	1	2
3	3	5	M	1	4	0	1
4	1	5	2	M	0	3	1
5	9	6	0	3	M	1	1
6	1	8	1	2	1	M	0
7	4	6	2	3	5	0	M

Такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент:

d_j = min(i) d_ij

i j	1	2	3	4	5	6	7
1	M	5	4	11	0	2	3
2	2	M	7	8	0	1	2
3	3	5	M	1	4	0	1
4	1	5	2	M	0	3	1
5	9	6	0	3	M	1	1
6	1	8	1	2	1	M	0
7	4	6	2	3	5	0	M
dj	1	5	0	1	0	0	0

После вычитания минимальных элементов получаем полностью редуцированную матрицу, где величины d_i и d_j называются константами приведения.

i j	1	2	3	4	5	6	7
1	M	0	4	10	0	2	3
2	1	M	7	7	0	1	2
3	2	0	M	0	4	0	1
4	0	0	2	M	0	3	1
5	8	1	0	2	M	1	1
6	0	3	1	1	1	M	0
7	3	1	2	2	5	0	M