Лабораторная работа 3. МОТС-2.Лаб раб №3. Лабораторная работа 3 по дисциплине Математические основы теории систем Учебное пособие Математические основы теории систем,часть 2

• Название: Лабораторная работа 3 по дисциплине Математические основы теории систем Учебное пособие Математические основы теории систем,часть 2
• Анкор: Лабораторная работа 3
• Дата: 07.04.2023
• Размер: 98 Kb.
• Имя файла: МОТС-2.Лаб раб №3.doc
• Тип: Лабораторная работа; #1043620

Ф едеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ

(ТУСУР)

ЛАБОРАТОРНАЯ РАБОТА №3
по дисциплине «Математические основы теории систем»

(Учебное пособие «Математические основы теории систем»,часть 2,

автор Карпов А.Г., 2002 г.)

Вариант №11

Задание 1

Дано нелинейное дифференциальное уравнение:



Необходимо:

1. 
   Линеаризовать уравнение вблизи точки статического режима путем разложения в ряд Тейлора;
   
2. 
   Решить линеаризованное уравнение при нулевых начальных условиях;
   
3. 
   По линеаризованному уравнению записать передаточную функцию.
   

Решение
Для статического режима имеем: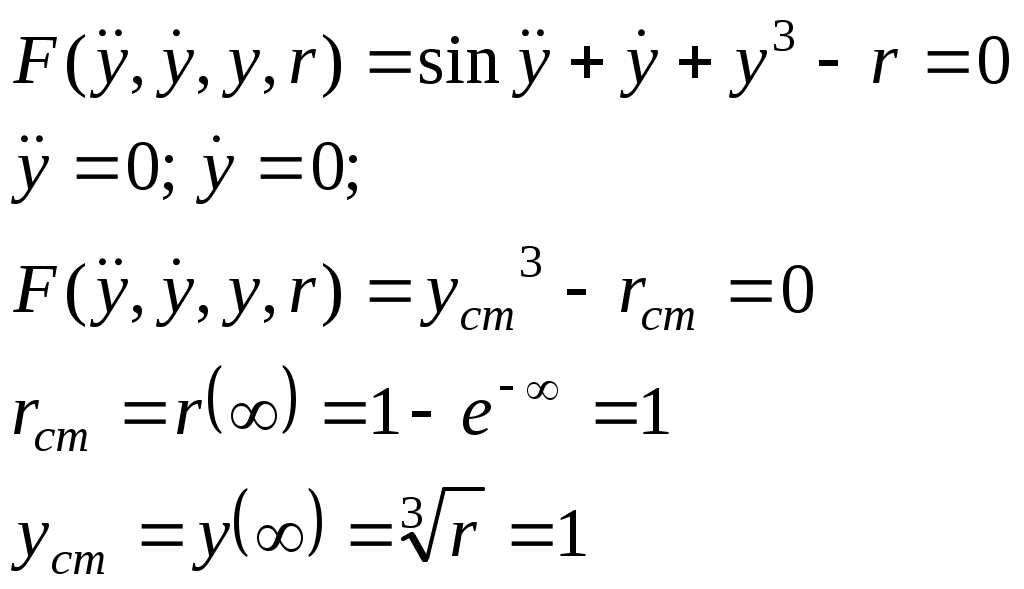


Частные производные в точке статического режима: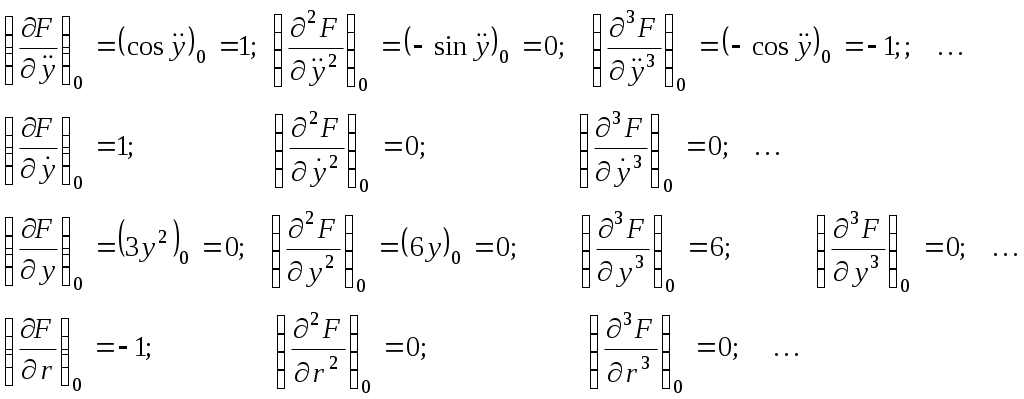



Пренебрегая членами разложения в ряд Тейлора выше первого порядка, получим линейное уравнение в вариациях: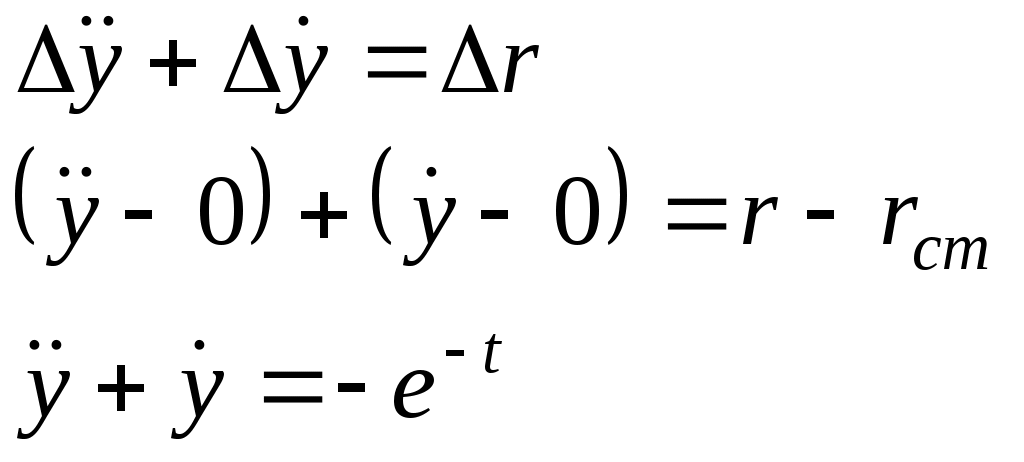

Корнями характеристического уравнения являются r₁=0 и r₂= -1. Вынуждающая функция является функцией специального вида, допускающей применение метода неопределенных коэффициентов.

Общим решением уравнения является


Частным решением уравнения является функция, подобная вынуждающей. Поскольку один из корней совпадает с коэффициентом показателя степени вынуждающей функции -e^-t , не6обходимо добавить резонансный множитель.



Подставляя эти выражения в линеаризованное уравнение, получаем: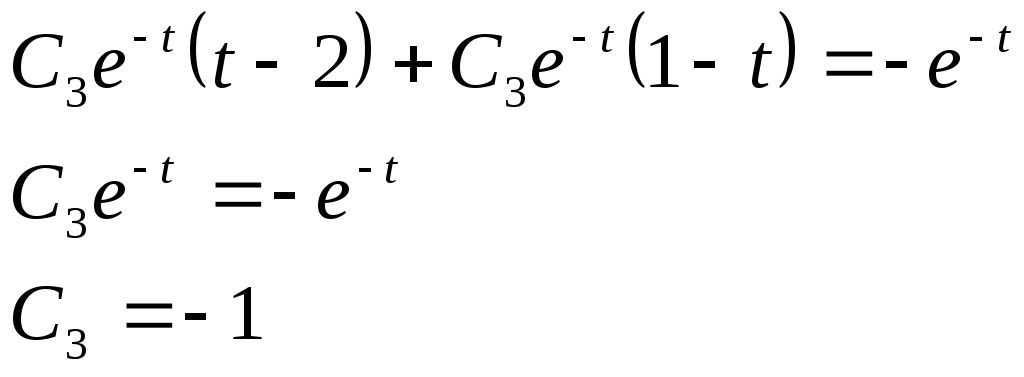


Т 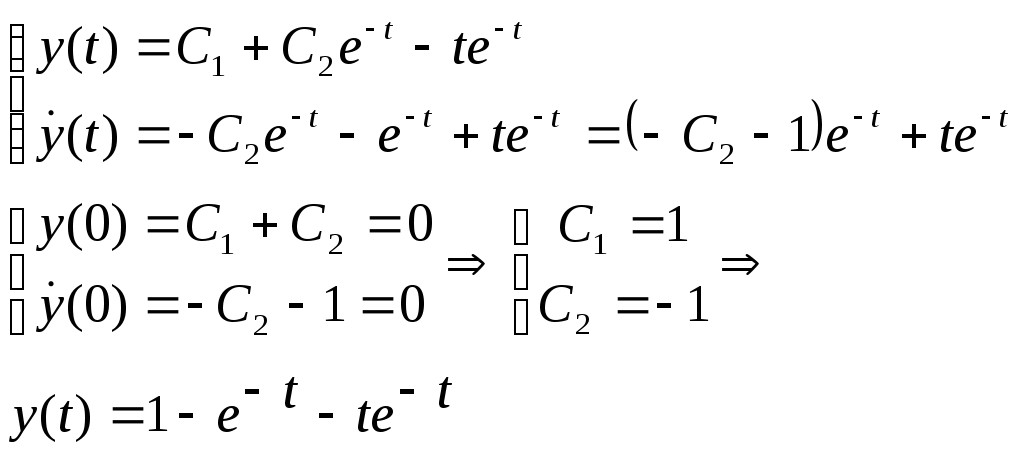аким образом, получаем полное решение как сумму общего и частного решений, а константы интегрирования получаются из начальных условий:

Вернувшись к уравнению в вариациях, представим его в операторной форме и получим передаточную функцию для отклонений: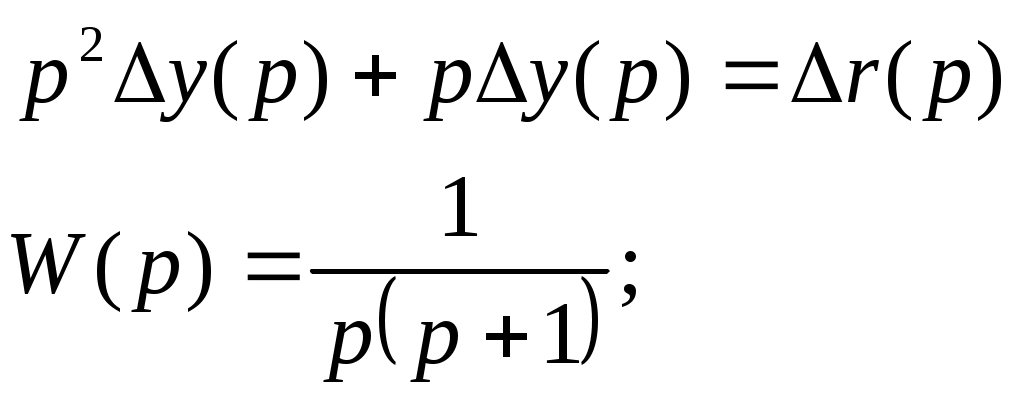


Задание 2

Используя свойства преобразования Лапласа и приложение 1, найти изображение по Лапласу для заданной функции —

Решение

Используя формулу Эйлера: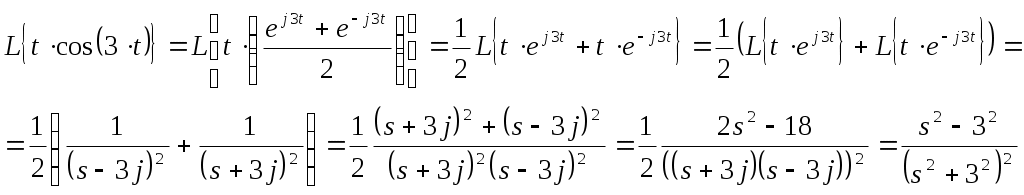



Задание 3

Дано уравнение в прямых разностях:



Необходимо:

1. 
   Перейти от уравнения в прямых разностях к уравнению с применением операторов сдвига;
   
2. 
   Решить это уравнение при нулевых начальных условиях;
   
3. 
   Записать импульсную передаточную функцию;
   
4. 
   Решить разностное уравнение с применением z-преобразования;
   

Решение.

Уравнение с оператором сдвига имеет вид: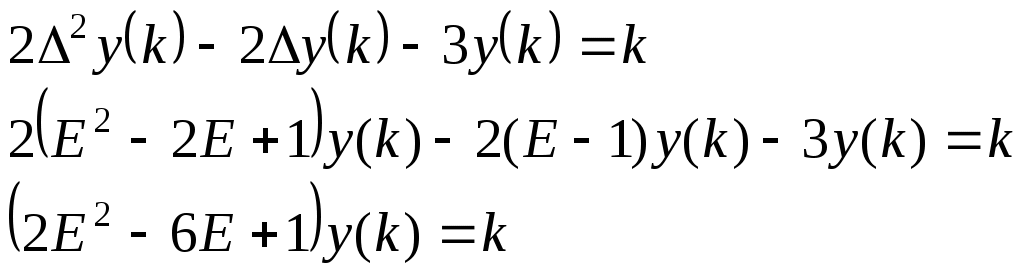


Характеристическое уравнение: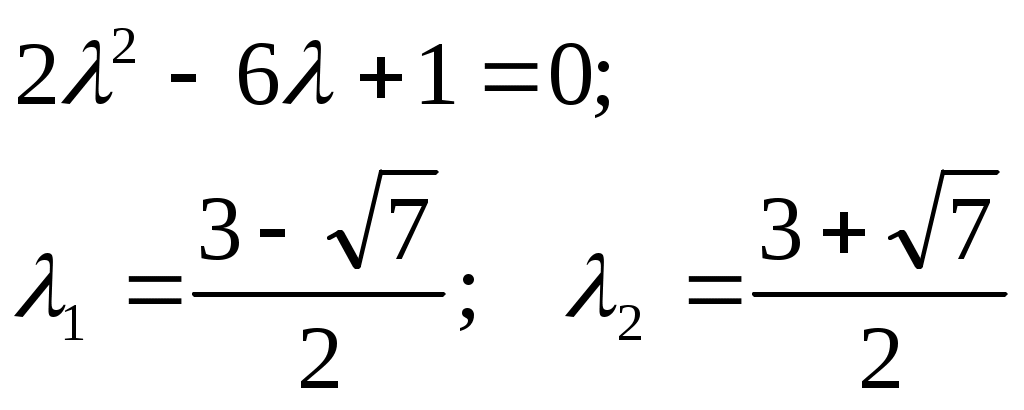



Поскольку корни действительны и различны, общее решение:



Поскольку правая часть специального вида (полином степени 1), частное решение ищем в виде,



Подставляя частное решение в исходное уравнение, находим: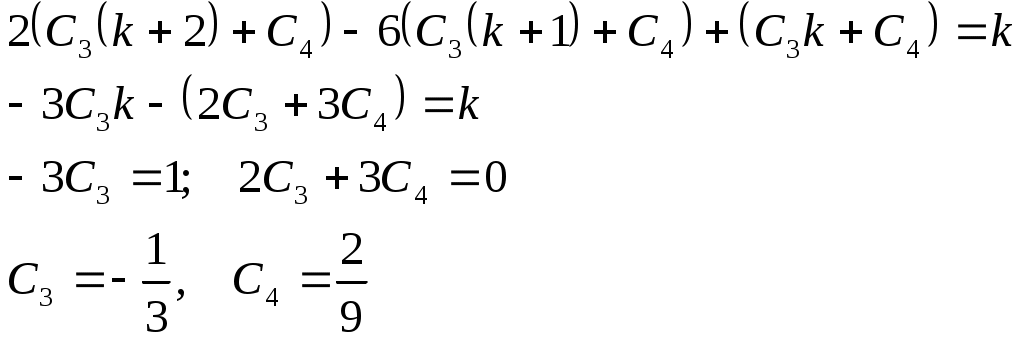


Из нулевых начальных условий k=0, y(0)=0, y(1)=0, находим коэффициенты общего решения: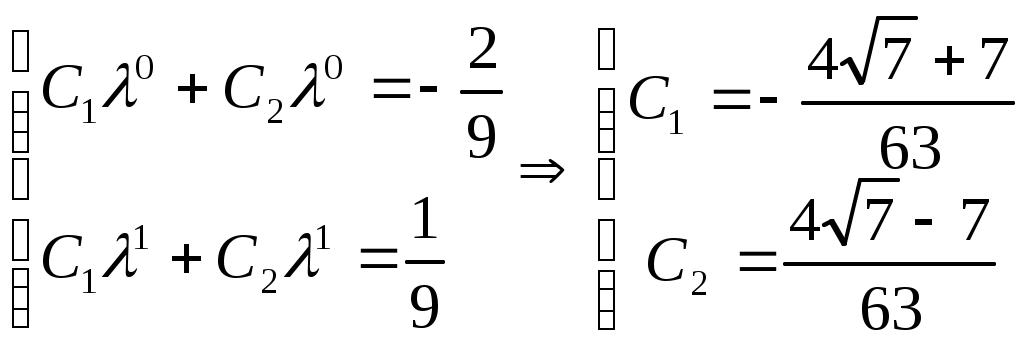



В итоге решением исходного уравнения будет ряд:



Импульсная передаточная функция находится из z-отображения исходного уравнения. При условии предварительно невозбужденной системы имеем: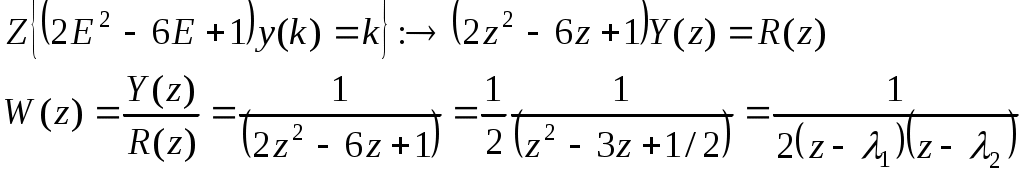


Выражение для выходной функции: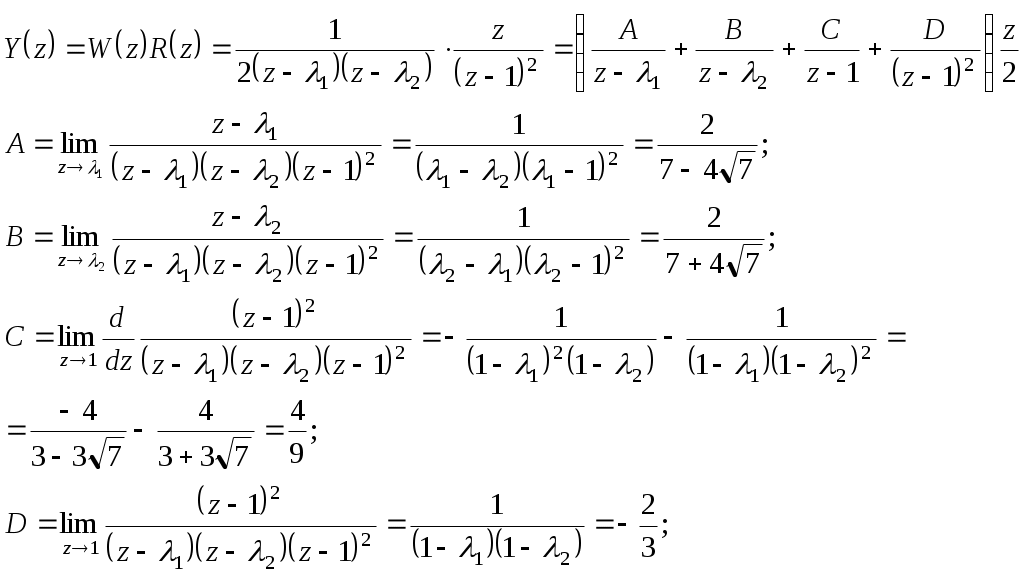

Таким образом, разложение на элементарные дроби и обратное z-преобразование дает: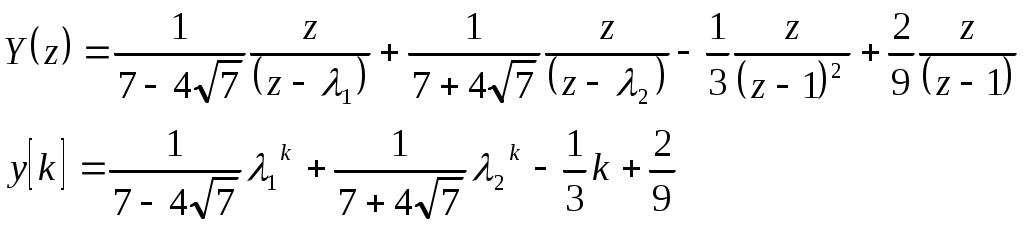




Задание 4

Используя свойства z-преобразования и приложение 1, найти z-изображение заданной функции te^{- t}
Решение
По теореме об умножении на экспоненту: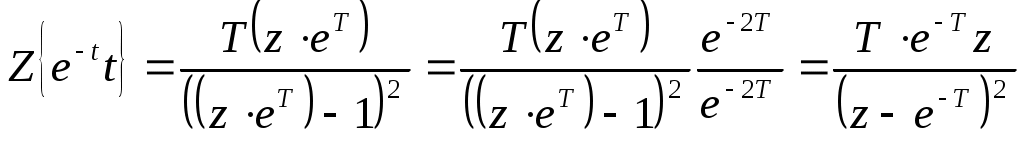





При Т=1, выражение упрощается: