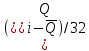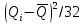Метрология. Лабораторная работа 3 По дисциплине Проверка справедливости и экспериментальное исследование основной аксиомы метрологии
 Скачать 60.46 Kb. Скачать 60.46 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования <<САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ>> Кафедра метрологии, приборостроения и управления качеством Лабораторная работа № 3 По дисциплине: «Проверка справедливости и экспериментальное исследование основной аксиомы метрологии» Тема работы: Методы и средства измерения линейных размеров Выполнили: ст. гр. ТПР-19 е / Плюхин И.А./ (группа) (подпись) (Ф.И.О.) Дата: ________________ Проверил: доцент /Смирнова Е.Е./ (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2022 Цель – изучение методики обработки многократного измерения. Содержание - обработка экспериментально полученных данных с целью проверки основной аксиомы метрологии. Объект. Анализ результатов опробывания руды полиметаллического месторождения. Задача. Требуется определить действительное значение параметра качества добываемой продукции.
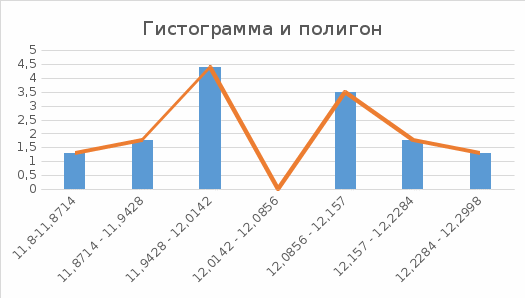
Среднеквадратичное отклонение. 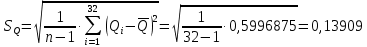 Вычисление критерия Граббса: 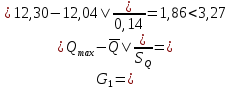 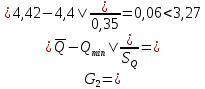 При n=32 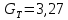 , так как , так как 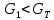 и и 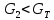 , то оба значения проходят проверку и не являются промахами , то оба значения проходят проверку и не являются промахами Проверка нормальности закона распределения результата измерения Для нормального закона распределение плотности вероятности описывается формулой: 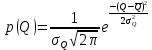 Такое распределение имеет колоколообразную форму Для поверки нормальности закона распределения случайных величин используются различные статические критерии согласия. Так как n=32, то имеем серию средних размеров, следовательно, используем составной критерий: 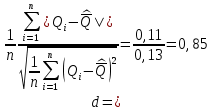 При n=32 условие 0,712<0,85<0,88 выполняется с вероятностью Р*=0,99 Проверим “хвосты” распределения: Для доверительной вероятности Р**=0,98 попавшими на “хвосты” распределения являются значения, для которых выполняется неравенство 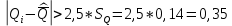 Так как таких значений нет, то гипотеза по 2-ой части составного критерия принимается Гипотеза принимается в целом с вероятностью: 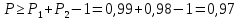 При 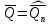 и и 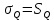 получим: получим: 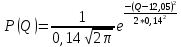
 P(Q) 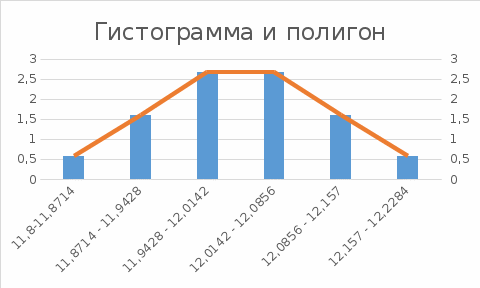 Определение доверительных границ результата измерения Расчет стандартного отклонения оценки среднего арифметического результатов измерения: 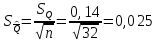 Определим доверительные границы результата: 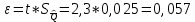 Границы доверительного интервала: 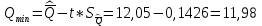 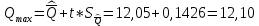 Интервал полученных значений: 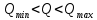 11,98 < Q < 12,10 Вывод Результат измерения является случайной величиной, подчиняется нормальному закону распределения вероятности со следующими оценками числовых характеристик: 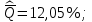 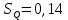 % % Результат измерения находится в доверительном интервале Q=[11,98 …12,10] с доверительной вероятностью P=0,97 |

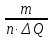
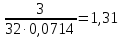
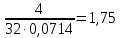
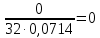
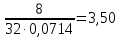
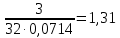
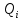
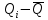
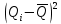
 /32
/32