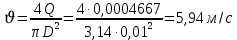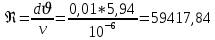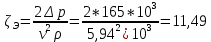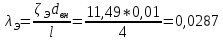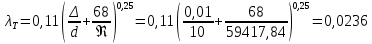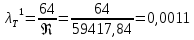Главная страница
Навигация по странице:

  • Схема установки

  • Краткие теоретические сведения

  • Таблицы данных

  • Обработка экспериментальных данных на примере первого испытания

    		•

    Определение гидравлической характеристики трубопровода. Лабораторная работа 3 Тема работы Определение гидравлической характеристики трубопровода


    Скачать 120.18 Kb.
    НазваниеЛабораторная работа 3 Тема работы Определение гидравлической характеристики трубопровода
    АнкорОпределение гидравлической характеристики трубопровода
    Дата30.11.2022
    Размер120.18 Kb.
    Формат файлаdocx
    Имя файлаzagotovka_lr_3.docx
    ТипЛабораторная работа
    #821950


    ЛАБОРАТОРНАЯ РАБОТА №3

    Тема работы: Определение гидравлической характеристики трубопровода .

    Цель работы – экспериментальное определение гидравлической характеристики длинного трубопровода.

    Схема установки

    Схема экспериментальной установки представлена на рисунке 1.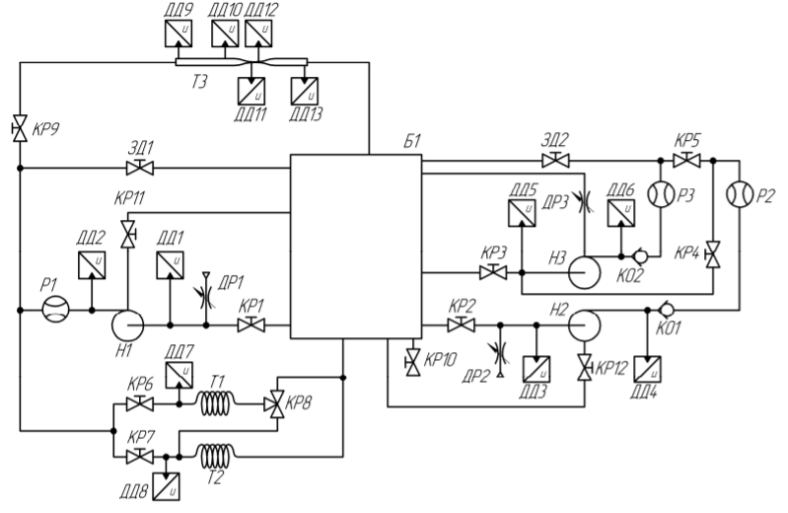



    Рис. 1. Схема учебного стенда «Насосы динамического типа»

    Краткие теоретические сведения

    Учитывая зависимость от соотношения линейных и местных потери, трубопроводы делятся на короткие и длинные, в зависимости от конструкции гидравлической системы – на простые и сложные.

    Короткие трубопроводы – это трубопроводы сравнительно небольшой длины, на которых смонтировано значительное количество местных сопротивлений и, в связи с этим, местные потери сопоставимы с линейными. Это, к примеру, системы объемных гидравлических приводов всех назначений, системы смазки различных устройств.

    Вместе с тем, это трубопроводы, некорректный расчет которых может вызвать отказ работы устройства.

    При расчете коротких трубопроводов учитываются как линейные, так и местные потери: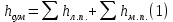



    Задачи решаются с применением уравнений неразрывности и Бернулли для потока реальной жидкости.

    В свою очередь длинные трубопроводы – это трубопроводы значительной длины, в которых линейные потери являются основными.

    При расчете таких трубопроводов определяются только линейные потери, а на местные добавляют 5-10% от линейных;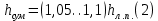



    Простые трубопроводы – это трубопроводы, как правило, одного диаметра не имеющие ответвлений.

    Сложные трубопроводы имеют различного рода ответвления или состоят из нескольких линий.

    Гидравлической характеристикой трубопровода принято называть зависимость напора, который крайне важно создать в трубопроводе для пропуска по нему определенного расхода, т.е. H=f(Q).

    Расчет потерь давления по длине исследуемого трубопровода проводится из уравнения Бернулли. Учитывая, что скоростной напор по длине трубопровода неизменен), потери давления определяются по формуле: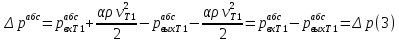



    Средняя скорость жидкости определяется по формуле: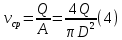



    где D – внутренний диаметр трубопровода, равный 10 мм.

    Критерий Рейнольдса определяется по формуле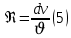



    где 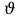– кинематическая вязкость воды, равная 10-6 м2/с.

    Из формулы Дарси-Вейсбаха величина коэффициента сопротивления трубопровода определяется как: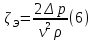



    Коэффициент гидравлического трения определяется по формуле: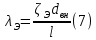



    где l – длина трубопровода, равная 4 м.

    Теоретическая величина коэффициента гидравлического трения в предположении турбулентного течения определяется по формуле Альтшуля: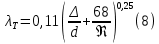



    и в предположении ламинарного режима по формуле Стокса: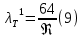



    Таблицы данных

    Табл. 1 – Экспериментальные и расчетные величины

    №
    f, Гц
    QН1,

    л/мин
    pвх Т1,

    кПа
    ϑср,

    м/с
    Re
    ζЭ
    λЭ
    λТ
    λТ1

    1
    50
    28
    203
    5,94
    59417,84
    11,499
    0,02874963
    0,0236
    0,0011

    2
    45,6
    25
    173
    5,31
    53051,65
    12,293
    0,03073395
    0,0240
    0,0012

    3
    40,1
    22
    138
    4,675
    46685,45
    12,663
    0,03165818
    0,0245
    0,0014

    4
    35,2
    19
    103
    4,03
    40319,25
    12,672
    0,03167979
    0,0250
    0,0016

    5
    29,7
    16
    73
    3,39
    33953,05
    12,665
    0,03166177
    0,0257
    0,0019

    6
    24,8
    13
    52
    2,76
    27586,86
    13,665
    0,03416402
    0,0267
    0,0023

    7
    20,9
    11
    38
    2,33
    23342,72
    13,948
    0,03486988
    0,0275
    0,0027


    Обработка экспериментальных данных на примере первого испытания

    Определение скорости движения жидкости в трубопроводе по формуле (4):
    (10)

    Определение значения числа Рейнольдса по формуле (5):
    (11)

    Определим величину коэффициента сопротивления трубопровода по формуле Дарси-Вейсбаха (6):
    (12)

    Определение коэффициента гидравлического трения по формуле (7):
    (13)

    Определение теоретической величины коэффициента гидравлического трения в предположении турбулентного течения по формуле Альтшуля (8):
    (14)

    Определение теоретической величины коэффициента гидравлического трения в предположении ламинарного режима по формуле Стокса (9):
    (15)



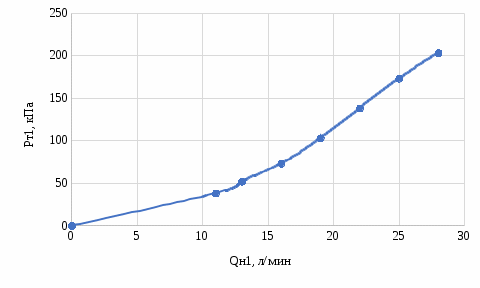    Рис. 2. Гидравлическая характеристика трубопровода

    Вывод: в ходе лабораторной работы была определена гидравлическая характеристика заданного длинного трубопровода, из нее можно понять, что для пропуска большего расхода необходимо создать большую разницу давлений. При уменьшении расхода уменьшается скорость течения жидкости и, соответственно, числа Рейнольдса. Коэффициент же гидравлического трения возрастает, причем его экспериментальные значения находятся ближе к теоретическим значениям для турбулентного режима, из чего можно сделать предположение, что в трубопроводе создается именно данный режим.

    написать администратору сайта