Лабораторная работа 3 устойчивостьлинейных систем с сосредоточенными и постоянными параметрами
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
|
Московский Авиационный Институт (Национальный Исследовательский Университет) Институт № 3 «Системы управления, информатика и электроэнергетика» Кафедра 301 «Системы автоматического и интеллектуального управления» Лабораторная работа № 3 УСТОЙЧИВОСТЬЛИНЕЙНЫХ СИСТЕМ С СОСРЕДОТОЧЕННЫМИ И ПОСТОЯННЫМИ ПАРАМЕТРАМИ Выполнила Студентка группы М3О-301Б-17 Пермикина С.С. Принял Преподаватель кафедры Белоногов В.Д. Москва 2019 Цель работы: изучить методы исследования устойчивости линейных систем с сосредоточенными и постоянными параметрами, оценить характер процессов управления в окрестности границы устойчивости САУ Определить с помощью критерия устойчивости Михайлова все возможные коэффициенты передачи, при которых нескорректированная система замкнутого типа оказывается на границе устойчивости Задания к лабораторной работе Определить с помощью критерия устойчивости Михайлова все возможные коэффициенты передачи, при которых нескорректированная система замкнутого типа оказывается на границе устойчивости Записать передаточные функции замкнутой системы и привести их к дробно-рациональному виду при следующих значениях параметра Ку: 1) Ку = 0.95*Кkrit 2) Ку=Кkrit 3) Ку=1.05*Кkrit 3. Построить ЛАЧХ и ЛФЧХ для разомкнутой СУ Структурная схема 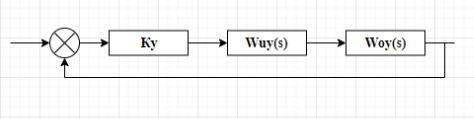 Выполнение работы Так как все элементы соединены между собой последовательно, а коэффициент ООС = 1, общая передаточная функция будет иметь вид: Возьмем Кy=1  Нет действительных решений, следовательно, система не устойчива по кр. Михайлова 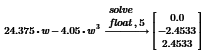 Так как Подставим эти значения в Re и получим точки, входящие в годограф (значения действительной части при нулевой мнимой) 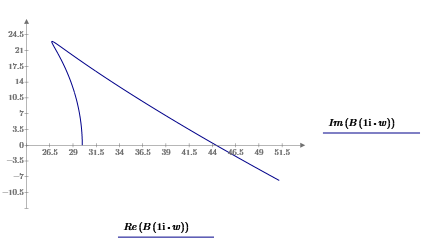 Данная система не устойчива по критерию Михайлова Найдем критическое значение частоты и коэффициента передачи Запишем и решим систему уравнений 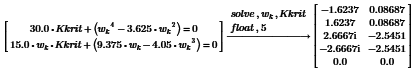 Тогда подходят следующие сочетания wk и Kkrit a) Ky=Kkrit1 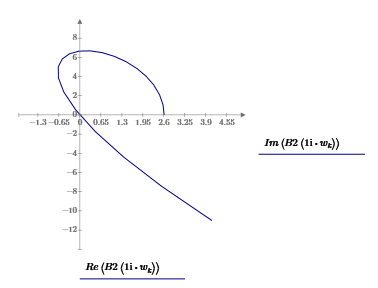 б) Ky=0.95*Kkrit1 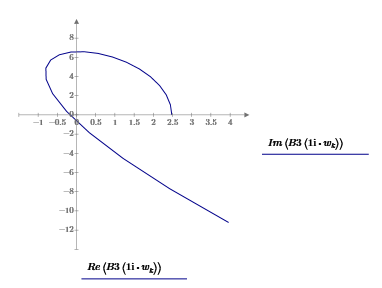 Так как рассматривается характеристическое уравнение 4 степени, годограф должен последовательно проходить через все четыре четверти для того, чтобы быть устойчивым. Так как это условие выполняется, данная система будет устойчива по кр. Михайлова в) Ky=1.05*Kkrit1 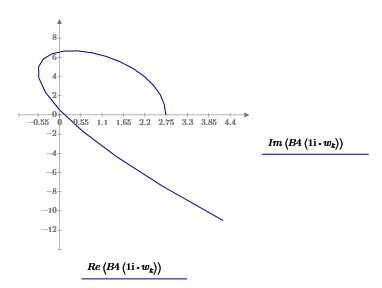 Так как рассматривается характеристическое уравнение 4 степени, годограф должен последовательно проходить через все четыре четверти для того, чтобы быть устойчивым. Так как это условие не выполняется, данная система будет не устойчива по кр. Михайлова Построить ЛАЧХ для замкнутой СУ 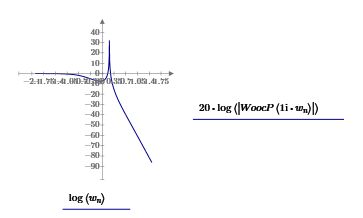 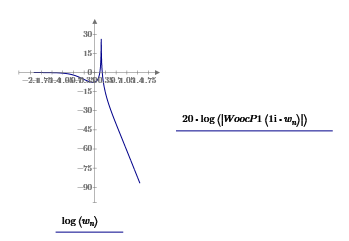 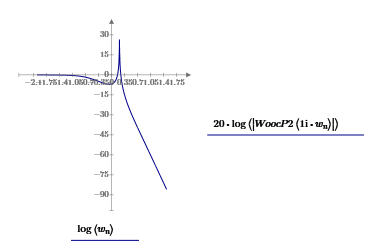 Построить ЛФЧХ для разомкнутой СУ 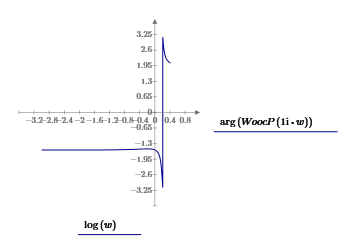 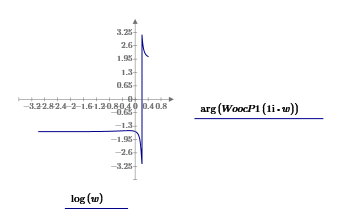 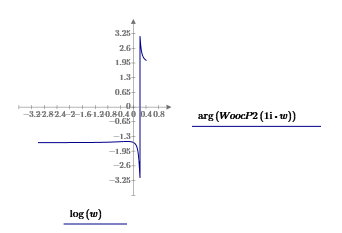 |
