Лабораторная работа 5-30 по Физике. Лабораторная работа 30 явление самоиндукции
 Скачать 52 Kb.
|
Лабораторная работа № 5.30ЯВЛЕНИЕ САМОИНДУКЦИИЦель работы: ознакомиться с явлением самоиндукции; изучить зависимость постоянной времени электрической цепи, состоящей из катушки индуктивности и омического сопротивления, от величины сопротивления; определить величины индуктивности катушки и магнитной проницаемости сердечника соленоида. Приборы и принадлежности: генератор прямоугольных импульсов, электронный осциллограф, лабораторный стенд, магазин сопротивлений. Краткие теоретические сведенияЯвление самоиндукции заключается в возникновении ЭДС индукции в электрической цепи, обладающей индуктивностью, при изменении в ней электрического тока. Электрический ток, протекая по проводникам, создаёт в окружающем пространстве магнитное поле. Магнитный поток этого поля, сцеплённый с контуром проводника (потокосцепление самоиндукции), вычисляется по формуле  , (1)где N – число витков соленоида. Интегрирование в (1) ведётся по сечению соленоида. При слабых магнитных полях и неизменных параметрах контура, как правило, потокосцепление пропорционально силе тока: =LI. (2) Коэффициент пропорциональности L называется индуктивностью контура. Индуктивность характеризует способность проводящего контура создавать потокосцепление собственного магнитного поля с контуром проводника. Она численно равна потокосцеплению при силе тока, равной единице: L=I. (3) Индуктивность измеряется в генри: 1Гн=Вб/А. Индуктивность - скалярная величина, не зависящая от протекающего по контуру тока (в отсутствии ферромагнитных сред). Согласно закону электромагнитной индукции, возникающая в цепи ЭДС самоиндукции равна скорости изменения потокосцепления самоиндукции: s= - ddt. (4) Если L - величина постоянная, то из (2) получаем i = - L dI/dt. (5) Знак минус отражает тот факт, что в проводящем контуре ЭДС самоиндукции всегда препятствует изменению электрического тока, т.е. стремится поддерживать силу тока неизменной. Самоиндукция в электромагнетизме играет ту же роль, что и инерция в механике. Используя выражения (1) и (3), можно получить формулу для индуктивности соленойда, выбрав поверхность интегрирования, перпендикулярную осевой линии соленойда. L=N2Sl (6) где 0=4 10-7Гн/м - магнитная проницаемость сердечника соленойда, N - общее число витков, S - площадь поперечного сечения, l- длина соленойда. Рассмотрим переходные процессы в индуктивно-резистивной цепи, которая состоит из омического сопротивления R, индуктивности L и источника ЭДС (рис.1). По закону Ома для замкнутой цепи =(+s)/R, (7) учитывая (5), получим дифференциальное уравнение первого порядка I R= - LdI/dt. (8) Д 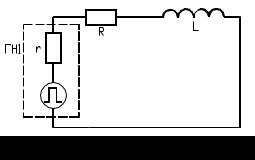 ля его решения (8) введём начальные условия: пусть при t=0, =0 и I=0; при t>0, =const и II(t). Найдём функциональную зависимость силы тока от времени. Для этого в (8) разделим переменные и проинтегрируем обе части уравнения, расставив пределы интегрирования с учётом начальных условий. 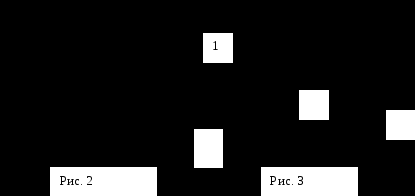(9)П  осле интегрирования I/R)[1 - exp(-Rt/L)]. (10) Согласно (10) и закону Ома для участка цепи, напряжение на активном сопротивлении R U=IR=[1-exp(-Rt/L)], (11) а на индуктивности L s=- exp(-Rt/L)=- exp(-t/). (12) Величину =L/R называют постоянной времени цепи, которая равняется времени, за которое интенсивность уменьшается в e раз, т.е. U=0.37 Umax , а при зарядке конденсатора  =0,63Umax. Она равна времени, за которое величина s уменьшится в 2,7 раза, а напряжение на сопротивлении возрастёт до величины 0,63. Графики зависимости U и s от времени показаны на рис. 2 и 3.Поскольку реальные источники обладают внутренним сопротивлением r, то постоянная времени =L/(R+r) или 1/=R/L+r/L. (13) Как видно из выражения (13), зависимость 1/ от R является линейной. Порядок выполнения работыДля определения постоянной времени собрана электрическая цепь, состоящая из генератора прямоугольных импульсов, омического сопротивления R, индуктивности L и осциллографа (рис. 4). В 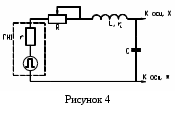 еличина активного сопротивления R задаётся с помощью магазина сопротивлений. 1. Включить приборы. 2. Установить на магазине сопротивлений значение R=100 Ом. 3. Установить частоту прямоугольных импульсов равной 400 Гц с помощью кнопки «F» на ГН, настроить осциллограф на режим наблюдения формы одного импульса с помощью кнопок «длит.» и «+, -». 4. Изучить зависимость постоянной времени от величины сопротивления R, изменяя ее в пределах от 100 до 500 Ом с шагом 100 Ом. Величина определяется методом изображенным на рис. 2. Предлагается устанавливать амплитуду сигнала на экране осциллографа равной пяти большим делениям шкалы (соответствует единице на рис. 2). Тогда уровень 0,63UR на рисунке будет примерно соответствовать трем большим делениям на экране осциллографа. Погрешность этого приближенного метода измерений не превышает 10 %. Результаты измерений занести в таблицу 1. Величина находится как число больших делений по горизонтальной оси шкалы экрана осциллографа, умноженное на длительность развертки. Таблица 1
5. Рассчитать величины 1/ для каждого значения R. 6. Построить график зависимости 1/=f(R) и убедиться, что зависимость является линейной. 7. Рассчитать величину индуктивности L либо по графику зависимости 1/f(R), где L является величиной, обратной тангенсу угла наклона прямой  , либо по методу наименьших квадратов (по согласованию с преподавателем).8. Определить магнитную проницаемость сердечника соленойда, используя формулу (6). S=0.64 см2, l=10 мм, N=300. Контрольные вопросы1. Явление самоиндукции. 2. Потокосцепление самоиндукции. 3. ЭДС самоиндукции. Индуктивность. Графики зависимости напряжения на резисторе и ЭДС самоиндукции от времени. 5. Постоянная времени цепи и ее зависимость от параметров контура. |