отчет 309_0. Лабораторная работа 309 получение и исследование света с различными состояниями поляризации

• Название: Лабораторная работа 309 получение и исследование света с различными состояниями поляризации
• Анкор: отчет 309_0
• Дата: 10.04.2022
• Размер: 269.5 Kb.
• Имя файла: 309_0 (1).doc
• Тип: Лабораторная работа; #458609

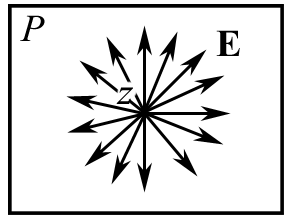
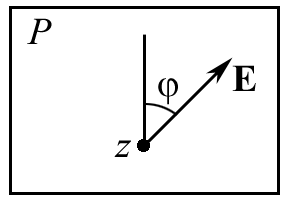
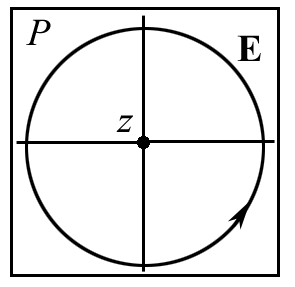
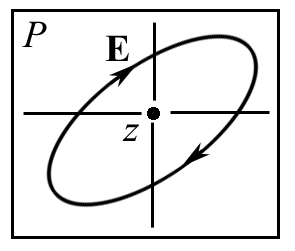
Лабораторная работа № 309
ПОЛУЧЕНИЕ И ИССЛЕДОВАНИЕ СВЕТА С РАЗЛИЧНЫМИ СОСТОЯНИЯМИ ПОЛЯРИЗАЦИИ
Цель работы: сформулировать гипотезу исследования, определить уровни исследования, изучить методы получения и анализа поляризованного света.

Приборы и принадлежности: источник теплового излучения (галогенная лампа накаливания) мощностью 100 Вт, монохроматор МУМ-2, приемник излучения (фотосопротивление), измерительный прибор (микроамперметр), поляризационные приспособления – поляризатор, анализатор, кристаллическая пластинка Δ/4, кристаллическая пластинка Δ/х, приборная стойка, оптический рельс.

Краткое теоретическое введение

Свет, в котором в каждый момент времени векторы Е и Н, будучи взаимно перпендикулярны друг другу, беспорядочно меняют свое направление в плоскости Р, перпендикулярной направлению распространения света (рис. 1), называется естественным. Если вектор Е или Н в световой волне колеблется только в одной плоскости Р (рис. 2), свет называется линейно или плоскополяризованным. Плоскость колебания вектора Е, называется плоскостью поляризации. Свет, в котором конец вектора Е описывает в пространстве винтовую траекторию, проекция которой в плоскости P, представляет окружность, называется поляризованным по кругу или циркулярно поляризованным (рис. 3). Если эта фигура эллипс, свет называется эллиптически поляризованным (рис. 4).

Рис. 1	Рис. 2	Рис. 3	Рис. 4

Получение линейно поляризованного света и его анализ

Линейно поляризованный свет получают из естественного света с помощью устройств, которые называются поляризаторами. Эти устройства свободно пропускают колебания, параллельные плоскости, которую называют плоскостью поляризации. Действие поляризаторов основывается на использовании либо закона Брюстера для отражения и преломления света на границе раздела двух прозрачных изотропных диэлектриков, либо явления двойного лучепреломления в одноосных анизотропных кристаллах (рис. 5). Из двоякопреломляющего кристалла выходят два линейно поляризованных луча, плоскости поляризации которых взаимно перпендикулярны.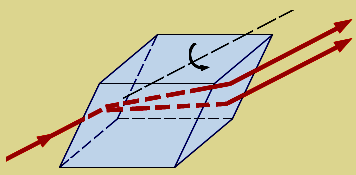



Рис. 5

Провести анализ линейно поляризованного света – значит определить положение его плоскости поляризации в пространстве.

Для анализа линейно поляризованного света используются приспособления, которые называются анализаторами. В качестве анализатора применяются те же устройства, которые служат для получения линейно поляризованного света.

Интенсивность света I_а, пропущенного анализатором, меняется в зависимости от угла , между плоскостью поляризации падающего на него линейно поляризованного света и плоскостью анализатора как

I_а = kI_pcos², (1)

где k – коэффициент прозрачности; I_p – интенсивность линейного поляризованного света, падающего на анализатор.

Формула (1) носит название закона Малюса (рис. 6). На рис. 6 приведена иллюстрация, поясняющая действие закона Малюса.



Рис. 6
Получение циркулярно поляризованного света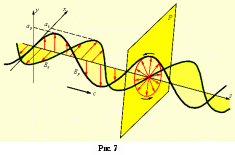




Из теории колебаний известно, что то или иное состояние поляризации получается при совместном действии двух взаимно перпендикулярных монохроматических световых волн равной частоты, распространяющихся в одном направлении z, при определенных отношениях их амплитуд А₁ и А₂ и разности фаз .

Так, циркулярно- поляризованная волна получается в случае выполнения условий

а) А₁ = А_2;

б) ,

что соответствует оптической разности хода складывающихся волн , где  длина волны монохроматического света, m = 0, 1, 2, …  (рис. 7).

Если хотя бы одно условие нарушается, результирующая световая волна будет или эллиптически, или линейно поляризованной.

Рассмотрим один из методов практического получения циркулярно поляризованного света.

Из изложенного следует, что для получения циркулярно поляризованного света необходимо:

1. 
   Получить две взаимно перпендикулярные с одинаковыми амплитудами А₁и А₂ монохроматические световые волны равной частоты, распространяющиеся в одном направлении.
   
2. 
   Создать между этими волнами разность фаз .
   

Для получения двух взаимно перпендикулярных линейно поляризованных волн, распространяющихся в одном направлении, необходимо пропустить монохроматический линейно поляризованный свет с длиной волны через плоскопараллельную пластинку K толщиной d. Пластинку вырезают из анизотропного кристалла таким образом, чтобы плоскость, на которую падает свет, была параллельна оптической оси М – Н кристалла (рис. 8). В этом случае говорят, что пластинка вырезана параллельно оптической оси. Линейно поляризованная световая волна, попадая в тонкую пластинку, создает две волны – обыкновенную и необыкновенную. Будучи линейно- поляризованными во взаимно перпендикулярных плоскостях, эти волны, распространяясь в пластинке с различными скоростями, приобретают на выходе из нее разность фаз , равную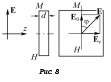

,

где n₀ и n_e – показатели преломления обыкновенной и необыкновенной волн в кристалле, соответственно.

Оптическая разность хода при этом равна

 = d (n₀ – n_e).

Для получения разности фаз между обыкновенной и необыкновенной волной, равной (2m + 1)/2, необходимо, чтобы пластинка имела определенную толщину d.

Толщина пластинки d определяется как

d(n₀ – n_e) = (2m + 1)/2.

При m = 0 толщина пластинки, создающая необходимую разность фаз, будет минимальная и равна

d(n₀ – n_e) = λ/4.

Кристаллическую пластинку, которая создает оптическую разность хода между обыкновенной и необыкновенной волной равной /4, называют «пластинка /4». Для получения одинаковых амплитуд у обыкновенной и необыкновенной волн, распространяющихся в кристаллической пластинке, необходимо, чтобы плоскость поляризации падающего света составляла с оптической осью М – Н пластинки угол , равный 45 (см. рис. 8).
Описание экспериментальной установки
Принципиальная схема экспериментальной установки, позволяющей получить и исследовать свет с р азличными состояниями поляризации, приведена на рис. 9. Монохроматический свет, получаемый при помощи монохроматора 1, пройдя выходную щель 3 попадает на собирающую линзу (на рис. не показана), которая фокусирует световой пучок на фотосопротивление. За линзой устанавливаются поляризационные приспособления, пройдя которые свет падает на фотосопротивление 4, величина сопротивления которого зависит от освещенности. Поэтому электрический ток, текущий по фотосопротивлению также будет зависеть от освещенности. Величина электрического тока регистрируется цифровым микроамперметром. Все лабораторные принадлежности установлены на оптическом рельсе 2.

В число поляризационных приспособлений входят два поляроида-поляризатора 5 и 6, кристаллическая пластинка 7. Все они помещаются во вращающиеся оправы с делениями, проградуированными в градусах. Остановимся кратко на тех функциях, которые выполняет каждая из основных частей установки: поляризационные приспособления, детектор светового излучения.

Монохроматор
Монохроматор в данной работе используется как прибор, с помощью которого из сплошного спектра длин световых волн выделяется узкий интервал длин волн, ограниченный значениями λ ±Δλ. Вращением отражательной дифракционной решетки монохроматора (посредством поворота регулировочной ручки) можно изменять значение λ, т.е. выделять спектральный интервал из разных участков сплошного спектра. Величина Δλ регулируется изменением входной и выходной щелей монохроматора. Необходимость использования света, близкого к монохроматическому, в условиях данной работы вытекает из того, что создание разности фаз между двумя световыми волнами возможна только по отношению к волнам одной частоты. Получение же света с определенным состоянием поляризации требует определенной разности фаз между складывающимися волнами. Кристаллическая пластинка «λ/4», очевидно является таковой только для определенного значения длины волны λ₀, которое и должно быть выделено монохроматором. Значение выделяемой монохроматической длины световой волны фиксируется в окошке торцевой части монохроматора.

Поляроид-поляризатор
Ближайший к источнику света поляроид позволяет получить линейно поляризованный свет. Ориентация поляроида относительно проходящего через него светового пучка не имеет значения. Прохождение света через два идеальных поляроида, гдеyy' – разрешенные направления поляроидов, показано на рис. 10.


Рис. 10
Кристаллическая пластинка «/4»
Кристаллическая пластинка «/4» нужна, прежде всего, для получения света, поляризованного по кругу. Она может применяться и для получения эллиптически поляризованного света. Пластинка «/4» может применяться и для анализа полученного с помощью другой пластинки эллиптически поляризованного света.

Ориентация оптической оси пластинки «/4» в пространстве имеет решающее значение, поэтому пластинка помещена во вращающуюся оправу с круговой шкалой. Дело в том, что ориентация оптической оси пластинки по отношению к плоскости поляризации падающего на нее линейно поляризованного света определяет амплитуды образующихся в ней двух волн – обыкновенной и необыкновенной. Пластинка дает волны равных амплитуд, нужные для получения света, поляризованного по кругу, только при ее определенной ориентации. Поворачивая оправу пластинки в другое положение, можно получить при помощи той же пластинки эллиптически поляризованный свет. Наконец, наличие в установке монохроматора позволяет использовать ту же пластинку для получения света, поляризованного эллиптически еще и другим способом. Пропуская через пластинку монохроматический свет иной длины волны, для которой пластинка не является пластинкой «/4», получим эллиптически поляризованный свет за счет отличного от /2 сдвига фаз между двумя линейно поляризованными световыми волнами в пластинке. В этом случае волны могут иметь равные амплитуды.

В данной экспериментальной установке используется одна кристаллическая пластинка, изготовленная из кристаллического кварца. Падающая вдоль нормали к пластинке световая волна продолжает распространяться в ней по прежнему направлению. Однако линейно поляризованная волна распадается на две линейно поляризованные, лежащие в двух взаимно перпендикулярных плоскостях. Это обыкновенная и необыкновенная волны. Эти две волны распространяются в одном направлении с разными скоростями.

Второй поляроид
Второй поляроид, стоящий на выходе поляризационного набора, является анализатором. Анализатор помещен во вращающуюся оправу с градуированной шкалой.
Детектор светового излучения
Детектор светового излучения представляет собой фотосопротивление, величина сопротивления которого зависит от освещенности. Электрический ток, который проходит по цепи, показанной на рис. 9. также зависит от освещенности фотосопротивления и регистрируется цифровым микроамперметром 7.

Упражнение 1.

Получение и анализ линейно поляризованного света. Проверка закона Малюса
Цель упражнения: познакомиться с одним из методов получения линейно поляризованного света и методом его анализа.
Задание

1. 
   Определить азимут плоскости поляризации линейно поляризованного света.
   
2. 
   Провести экспериментальную проверку закона Малюса.
   

Методика и техника измерений
Для получения линейно поляризованного света необходимо поместить поляроид-поляризатор под световой пучок непосредственно за линзой. Пропущенный поляроидом-поляризатором свет должен быть линейно поляризованным. Для проверки этого утверждения поместите перед детектором светового излучения поляроид-анализатор. При повороте анализатора вокруг оси микроамперметр показывает изменение интенсивности пропущенного анализатором света от максимального значения до значений, близких к нулю. Это говорит о том, что поляризатор дает линейно поляризованный свет.

Анализ линейно поляризованного света заключается в определении ориентации плоскости поляризации света в пространстве.

1. Зафиксируйте угловое положение поляризатора. Поворачивая анализатор вокруг оси на 1  2 деления, измерьте показания микроамперметра. Измерения необходимо провести на протяжении полного оборота анализатора, причем в точках с максимальной и минимальной интенсивностью пропущенного анализатором света, измерения необходимо провести многократно для повышения точности определения положения этих точек.

2. Проведите нормирование на единицу полученных показаний микроамперметра , для этого максимальное значение показаний микроамперметра нужно приравнять единице, а все другие значения будут равны отношению текущего показания микроамперметра к его максимальному значению.

3. Постройте на миллиметровой бумаге в полярных координатах график зависимости нормированных показаний микроамперметра от ориентации анализатора (в градусах). График линейно поляризованного света в полярных координатах имеет вид восьмерки. Азимут поляризации линейно поляризованного света определяется как угол между прямой, соединяющей два максимума, и осью абсцисс.

4. Постройте для проверки справедливости закона Малюса на этой же координатной сетке график зависимости cos² от угла . Совпадение экспериментального графика зависимости нормированных показаний микроамперметра от ориентации анализатора, то есть угла , говорит о справедливости закона Малюса (рис. 11).

Примечание. Для сравнения графиков рекомендуем принять за ось прямую, проведенную на экспериментальном графике, для которой угол  теоретического графика равен 0  180 .
Упражнение 2.

Получение циркулярно- поляризованного света
Цель упражнения: ознакомление с методом получения света, поляризованного по кругу.
З адание.

1. 
   Найти направление кристаллической оси кварцевой пластинки.
   

2. Получить циркулярно-поляризованный свет.
Методика и техника измерений

Для получения циркулярно- поляризованного света необходимо ориентировать кристаллическую кварцевую пластинку так, чтобы плоскость поляризации падающего на нее линейно поляризованного света составляла угол 45  с главным сечением пластинки. Для ориентации пластинки выполните следующие действия:

1. 
   Ориентируйте поляризатор и анализатор таким образом, чтобы их плоскости поляризации составляли угол 90 между собой. При этом микроамперметр должен зарегистрировать отсутствие света за анализатором.
   
2. 
   Поместите между поляризатором и анализатором кристаллическую кварцевую пластинку /4.
   
3. 
   Проведите измерение зависимости показаний микроамперметра от ориентации кварцевой пластинки на протяжении одного полного оборота вращения пластинки. Измерения проводите через (1  2) деления шкалы. Положения пластинки (а их четыре), в которых микроамперметр дает показания, близкие к нулю, промерьте многократно, так как от точности определения этих положений зависит отклонение состояния поляризации от кругового.
   
4. 
   Постройте в полярных координатах график зависимости показаний микроамперметра, нормированных на единицу, от ориентации кварцевой пластинки.
   
5. 
   Проведите на полученном графике две прямые через точки, соответствующие минимальным показаниям микроамперметра. Пометьте концы одной прямой буквами ₁ – ₂, а концы другой ₁ – ₂ (рис. 12). Предварительные исследования кристаллической пластинки показали, что прямую линию ₁ – ₂ необходимо провести через точки на графике, первая из которых ₁ имеет минимальное угловое значение (справа от 0).
   
6. 
   Поверните оправу пластинки, установив на ней отсчет, соответствующий биссектрисе угла ₁0 _1. Теперь пластинка ориентирована, то есть амплитуды получающихся в ней двух линейно поляризованных волн будут равны. БОЛЬШЕ ПЛАСТИНКУ НЕ ТРОГАТЬ!
   
7. 
   Поверните анализатор на один оборот. Если при этом показания микроамперметра меняются на величину более чем на 10 %, это означает, что длина волны монохроматического света, падающего на пластинку, не соответствует той, для которой пластинка является «пластинкой /4».
   
8. 
   Измените длину волны света, падающего на пластинку. Если при этом показания микроамперметра будут меняться на величину большую, чем 10%, то длину волны нужно изменить в обратную сторону. Подбор необходимой длины волны необходимо проводить до тех пор, пока показания микроамперметра станут меняться на величину не большую 10%.
   
9. 
   Нормируйте полученные показания микроамперметра на единицу и постройте в полярных координатах график зависимости тока от ориентации кварцевой пластинки, не меняя при этом ориентаций поляризатора и анализатора.
   

Вопросы и задания для самостоятельной работы
1. Дайте схему получения линейно, эллиптически и циркулярно поляризованного света.

2. Опишите известные способы получения и поляризованного света.

3. Как изготавливаются пластинки «/4» и с какой точностью?

4. Как из линейно поляризованного света получить циркулярно или эллиптически поляризованный свет?

5. Почему обыкновенный и необыкновенный лучи, полученные от естественного света, не являются когерентными?

6. Почему в анизотропном кристалле возникает множество волн?

7. Какие действия нужно предпринять, чтобы найти различия в свойствах обыкновенного и необыкновенного лучей?

8. Как изготовить пластинку в «полволны»?

9. Каким образом можно отделить обыкновенный луч от необыкновенного луча?

10. Какие индикаторы можно использовать для анализа света, прошедшего анализатор?

11. Каким методом можно измерить показатель преломления обыкновенного и необыкновенного лучей?

12. Почему основания призмы Николя составляет угол 68 с боковыми ребрами (вместо 71 у естественного кристалла)?

13. По какому принципу рассчитывают углы в призме Николя?

14. Плоские волны в анизотропном кристалле поперечны в отношении векторов D и Н. Почему они не поперечны в отношении вектора Е?

15. Почему при вращении исландского шпата вокруг главной оптической оси одно изображение любого предмета движется по кругу вокруг другого?

16. Можно ли заменить канадский бальзам слоем воздуха?

17. Как соотносятся метод Брюстера и метод двойного лучепреломления?

18. Какая дополнительная разность фаз вносится между обыкновенным и необыкновенным лучами, если их пропускать через пластинку /4, /2?

19. Как отличить друг от друга смесь естественного света с линейно поляризованным светом?

20. В каком случае линейно поляризованный луч на выходе из кристаллической пластинки превращается в эллиптически поляризованный?

21. Назовите условия, необходимые для наблюдения интерференции поляризованных лучей.

22. Каким образом можно обнаружить оптическую анизотропию тел?

23. Если электрическое поле параллельно диэлектрической оси кристалла, то распространение волн в анизотропном кристалле аналогично данному процессу в изотропном кристалле. Почему?

24. Как связана амплитуда колебаний вектора D преломленной волны и амплитуда падающей волны Е?

25. Объясните закон Брюстера, применив механизм излучения диполя.