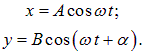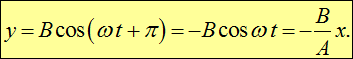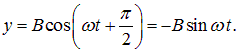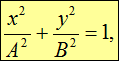СРС 10 Тартипов Р БТ 103. Конспект Тема Сложение взаимно перпендикулярных колебаний. Эллиптически поляризованные колебания. Частные случаи эллиптически поляризованных колебаний
 Скачать 36.08 Kb.
|
|
Конспект Тема «Сложение взаимно перпендикулярных колебаний. Эллиптически поляризованные колебания. Частные случаи эллиптически поляризованных колебаний» Рассмотрим сложение двух гармонических колебаний одинаковой частоты  , происходящих во взаимно перпендикулярных направлениях вдоль осей x и y. Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю:
где  — разность фаз обоих колебаний. Найдем уравнение траектории колеблющейся материальной точки, то есть функцию . Рассмотрим сначала частные случаи. Пусть разность фаз равна нулю:  . Тогда
то есть траектория точки представляет собой прямую. Аналогичная траектория получится при колебаниях с разностью фаз 
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет довольно сложный вид. Замкнутые траектории, описываемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, возникают тогда, когда отношение частот складываемых колебаний есть рациональное число, называются такие траектории фигурами Лиссажу. При разности фаз  находим:
Из верхней и нижней формул следует уравнение эллипса:
причем точка движется по часовой стрелке (для стандартного направления осей: ось ОХ — направо, ось ОУ — вверх). При разности фаз  находим:
Это приводит к той же эллиптической траектории (1.59), только вращение в этом случае происходит против часовой стрелки. Если амплитуды колебаний по осям х и у одинаковы (  ), то из (1.59) получается круговая траектория.В общем случае произвольной разности фаз траектория также будет представлять собой эллипс, но с повернутыми осями.Эллиптически поляризованной называют поперечную волну, в которой траектория каждой колеблющейся частицы за период колебаний имеет вид эллипса, лежащего в плоскости, перпендикулярной направлению распространения волны. Такая поляризация волны возникает, когда колебания частиц в двух компонентах поперечной волны со взаимно перпендикулярным направлением колебаний сдвинуты по фазе. Именно такое обстоятельство возникает вследствие изменения фазы отражения вертикально поляризованной волны от свободной границы при условии > |
