Исследование пассивных цепей при гармоническом воздействии на постоянной частоте. Отчет_лабораторная 32_вариант 11. Лабораторная работа 32 Исследование пассивных цепей при гармоническом воздействии на постоянной частоте Выполнила студентка Группы бст 0000
 Скачать 1.43 Mb. Скачать 1.43 Mb.
|
|
Минцифры России Ордена трудового красного знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» Кафедра Теория электрических цепей Лабораторная работа №32 «Исследование пассивных цепей при гармоническом воздействии на постоянной частоте» Выполнила студентка Группы БСТ 0000 Фамилия И.О. Проверил доц. Микиртичан А.Г. Оглавление1 Цель работы 3 2 Задание для лабораторной работы 3 3 Предварительный расчет 3 4. Машинный эксперимент 11 4.1. Исследование модуля и фазы комплексного сопротивления С-цепи. 11 4.2. Исследование модуля и фазы комплексного сопротивления RС-цепи. 13 4.3. Исследование модуля и фазы комплексного напряжения на конденсаторе RC-цепи. 15 4.4. Исследование модуля и фазы комплексного сопротивления L-цепи. 16 4.5. Исследование модуля и фазы комплексного сопротивления RL-цепи. 17 4.6. Исследование модуля и фазы комплексного напряжения на катушке RL-цепи. 19 Выводы. 20 Вопросы для самопроверки 21 1 Цель работыС помощью программы Micro-Cap исследовать электрический режим конденсатора и катушки индуктивности в цепях гармонического тока. Сравнить полученные характеристики с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем. 2 Задание для лабораторной работыИзучить основные положения ТЭЦ о частотных характеристиках электрических цепей, о комплексных сопротивлениях RC- и RL-цепей. Познакомится с возможностями схемотехнического моделирования. Выполнить предварительный расчет, письменно ответить на вопросы для самопроверки. 3 Предварительный расчет3.1. Расчет в алгебраической форме комплексного сопротивления конденсатора 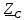 (рис.1), определение его полного сопротивления (рис.1), определение его полного сопротивления 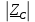 и аргумента arg и аргумента arg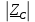 на пяти частотах 1, 2, 3, 4 и 5 кГц, если С = 37 нФ. на пяти частотах 1, 2, 3, 4 и 5 кГц, если С = 37 нФ.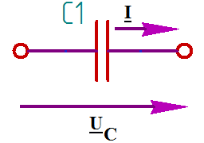 Рис.1 Формулы для расчета: 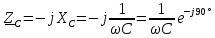 – комплексное сопротивление конденсатора; – комплексное сопротивление конденсатора;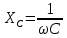 – емкостное сопротивление конденсатора; – емкостное сопротивление конденсатора;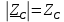 – модуль комплексного сопротивления конденсатора; – модуль комплексного сопротивления конденсатора;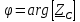 – аргумент(фаза) комплексного сопротивления конденсатора; – аргумент(фаза) комплексного сопротивления конденсатора;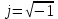 - мнимая единица; - мнимая единица;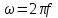 – угловая частота; – угловая частота; f – частота. Полученные величины занесли в таблицу 1 предварительного расчета. Таблица 1 – Расчет сопротивления конденсатора
Векторная диаграмма показана на рис. 2. 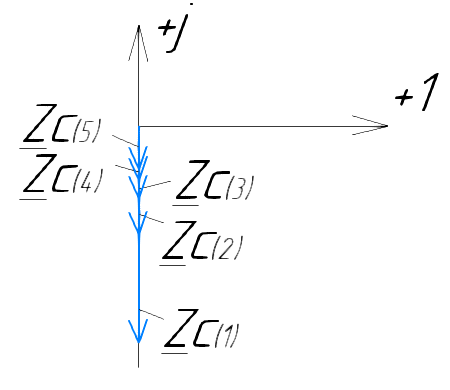 Рис.2 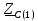 - сопротивление конденсатора на частоте f = 1 кГц, - сопротивление конденсатора на частоте f = 1 кГц, 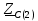 - сопротивление конденсатора на частоте f = 2 кГц, - сопротивление конденсатора на частоте f = 2 кГц, 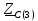 - сопротивление конденсатора на частоте f = 3 кГц, - сопротивление конденсатора на частоте f = 3 кГц, 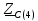 - сопротивление конденсатора на частоте f = 4 кГц, - сопротивление конденсатора на частоте f = 4 кГц, 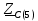 - сопротивление конденсатора на частоте f = 5 кГц. - сопротивление конденсатора на частоте f = 5 кГц.3.2. Расчет в алгебраической форме комплексного сопротивления 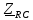 RC-цепи (рис.3) для пяти частот 1, 2, 3, 4, 5 кГц. Определение его полного сопротивления и аргумента, если R = 2800 Ом, С = 37 нФ. RC-цепи (рис.3) для пяти частот 1, 2, 3, 4, 5 кГц. Определение его полного сопротивления и аргумента, если R = 2800 Ом, С = 37 нФ.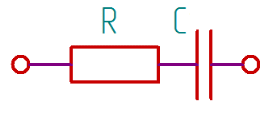 Рис.3 Формулы для расчета: 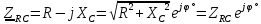 – комплексное сопротивление RC-цепи; – комплексное сопротивление RC-цепи;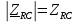 – модуль комплексного сопротивления двухполюсника; – модуль комплексного сопротивления двухполюсника;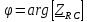 – аргумент (фаза) комплексного сопротивления двухполюсника; – аргумент (фаза) комплексного сопротивления двухполюсника;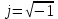 - мнимая единица; - мнимая единица;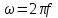 – угловая частота; – угловая частота; f – частота. Полученные величины занесли в таблицу 2. Таблица 2 – Расчет полного сопротивления RC-цепи
Векторная диаграмма показана на рис.4. 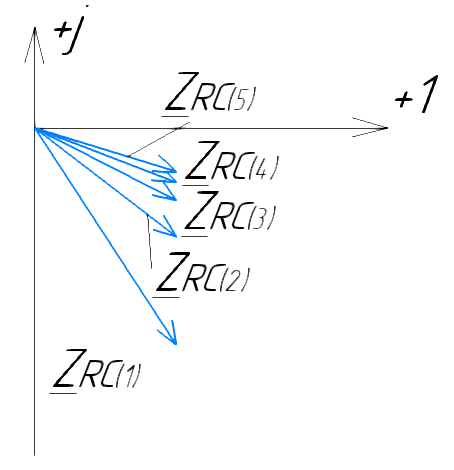 Рис.4 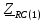 - комплексное сопротивление RC-цепи на частоте f = 1 кГц, - комплексное сопротивление RC-цепи на частоте f = 1 кГц, 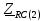 - комплексное сопротивление RC-цепи на частоте f = 2 кГц, - комплексное сопротивление RC-цепи на частоте f = 2 кГц, 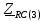 - комплексное сопротивление RC-цепи на частоте f = 3 кГц, - комплексное сопротивление RC-цепи на частоте f = 3 кГц, 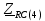 - комплексное сопротивление RC-цепи на частоте f = 4 кГц, - комплексное сопротивление RC-цепи на частоте f = 4 кГц, 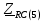 - комплексное сопротивление RC-цепи на частоте f = 5 кГц. - комплексное сопротивление RC-цепи на частоте f = 5 кГц.3.3. Расчет напряжения на конденсаторе 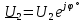 , если , если 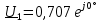 на частотах 1, 2, 3, 4, 5 кГц, определение его модуля и фазы (рис.5). на частотах 1, 2, 3, 4, 5 кГц, определение его модуля и фазы (рис.5).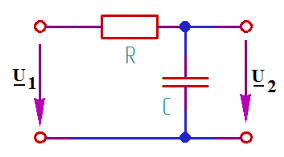 Рис.5 Формулы для расчета: 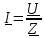 – комплексный ток; – комплексный ток;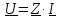 – комплексное падение напряжения; – комплексное падение напряжения;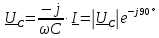 - комплексное напряжение на конденсаторе. - комплексное напряжение на конденсаторе.Полученные данные занесли в таблицу 3. Таблица 3 – Расчет напряжения на конденсаторе
3.4. Расчет в экспоненциальной форме комплексного сопротивления катушки индуктивности 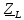 (рис.6) для пяти частот 1, 2, 3, 4, 5 кГц. Определение ее полного сопротивления и аргумента, если L = 28 мГн. (рис.6) для пяти частот 1, 2, 3, 4, 5 кГц. Определение ее полного сопротивления и аргумента, если L = 28 мГн.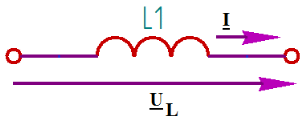 Рис.6 Формулы для расчета: 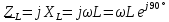 – комплексное сопротивление катушки; – комплексное сопротивление катушки;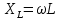 – индуктивное сопротивление катушки; – индуктивное сопротивление катушки;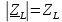 – модуль комплексного сопротивления катушки; – модуль комплексного сопротивления катушки;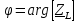 – аргумент (фаза) комплексного сопротивления катушки; – аргумент (фаза) комплексного сопротивления катушки;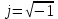 - мнимая единица; - мнимая единица;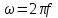 – угловая частота; – угловая частота; f – частота. Полученные данные занесли в таблицу 4. Таблица 4 – Расчет сопротивления катушки индуктивности
Векторная диаграмма (рис.7). 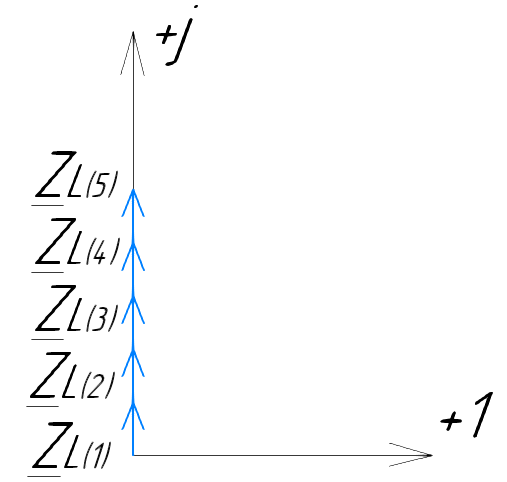 Рис.7 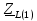 - комплексное сопротивление катушки на частоте f = 1 кГц, - комплексное сопротивление катушки на частоте f = 1 кГц,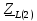 - комплексное сопротивление катушки на частоте f = 2 кГц, - комплексное сопротивление катушки на частоте f = 2 кГц, 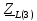 - комплексное сопротивление катушки на частоте f = 3 кГц, - комплексное сопротивление катушки на частоте f = 3 кГц, 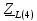 - комплексное сопротивление катушки на частоте f = 4 кГц, - комплексное сопротивление катушки на частоте f = 4 кГц, 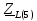 - комплексное сопротивление катушки на частоте f = 5 кГц. - комплексное сопротивление катушки на частоте f = 5 кГц.3.5. Расчет в алгебраической форме комплексного сопротивления 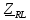 RL-цепи (рис.8) для пяти частот 1, 2, 3, 4, 5 кГц. Определение его полного сопротивления и аргумента, если R = 2800 Ом, L = 28 мГн. RL-цепи (рис.8) для пяти частот 1, 2, 3, 4, 5 кГц. Определение его полного сопротивления и аргумента, если R = 2800 Ом, L = 28 мГн.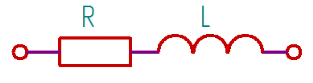 Рис.8 Формулы для расчета: 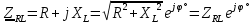 – комплексное сопротивление RL-цепи; – комплексное сопротивление RL-цепи;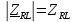 – модуль комплексного сопротивления двухполюсника; – модуль комплексного сопротивления двухполюсника;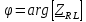 – аргумент (фаза) комплексного сопротивления двухполюсника; – аргумент (фаза) комплексного сопротивления двухполюсника;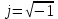 - мнимая единица; - мнимая единица;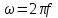 – угловая частота; – угловая частота; f – частота. Полученные данные занесли в таблицу 5. Таблица 5 – Расчет полного сопротивления RL-цепи
Векторная диаграмма показана на рис.9. 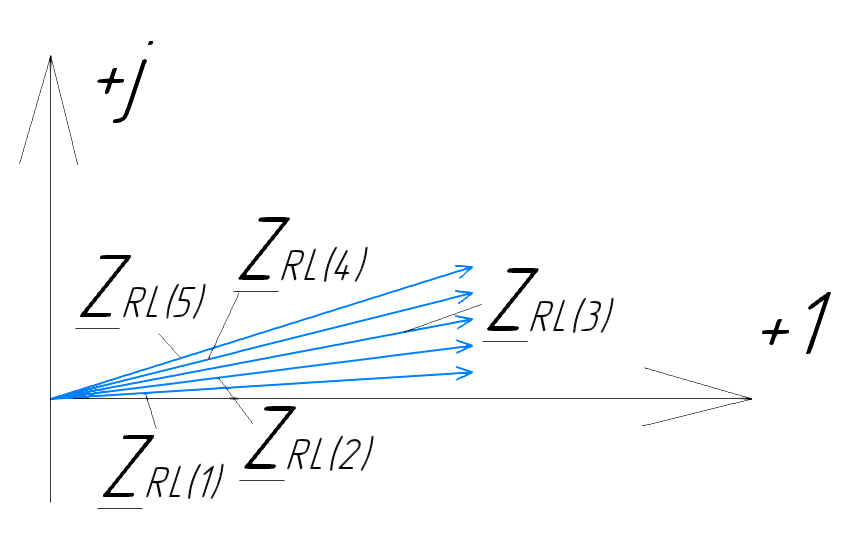 Рис.9 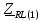 - комплексное сопротивление RL-цепи на частоте f = 1 кГц, - комплексное сопротивление RL-цепи на частоте f = 1 кГц, 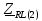 - комплексное сопротивление RL-цепи на частоте f = 2 кГц, - комплексное сопротивление RL-цепи на частоте f = 2 кГц, 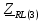 - комплексное сопротивление RL-цепи на частоте f = 3 кГц, - комплексное сопротивление RL-цепи на частоте f = 3 кГц, 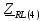 - комплексное сопротивление RL-цепи на частоте f = 4 кГц, - комплексное сопротивление RL-цепи на частоте f = 4 кГц, 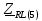 - комплексное сопротивление RL-цепи на частоте f = 5 кГц. - комплексное сопротивление RL-цепи на частоте f = 5 кГц.3.6. Расчет напряжения на катушке индуктивности 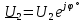 , если , если 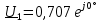 для пяти частот 1, 2, 3, 4, 5 кГц, определение его модуля и фазы (рис.10). для пяти частот 1, 2, 3, 4, 5 кГц, определение его модуля и фазы (рис.10).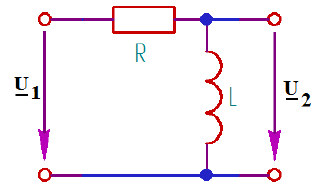 Рис. 10 Полученные данные занесли в таблицу 6. Таблица 6 – Расчет напряжения на катушке индуктивности
4. Машинный эксперимент4.1. Исследование модуля и фазы комплексного сопротивления С-цепи.Собираем схему с источником синусоидального напряжения и конденсатором (рис.11). 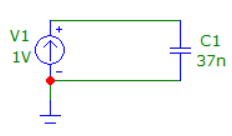 Рис. 11 – Схема для исследования модуля и фазы комплексного сопротивления С-цепи 4.1.1. Построение зависимости модуля сопротивления С-цепи от частоты. В меню Analysis выбрали команду AC…. В окне AC Analysis Limits устанавливаем параметры (рис.12). 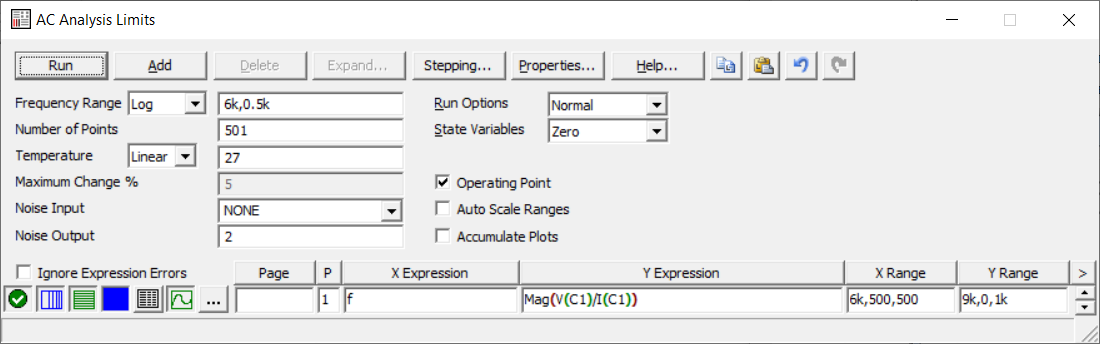 Рис. 12 На рисунке 13 изображен график зависимости модуля комплексного сопротивления конденсатора от частоты. На графике отмечены величины модуля комплексного сопротивления конденсатора при f = 1 кГц и f = 2 кГц. 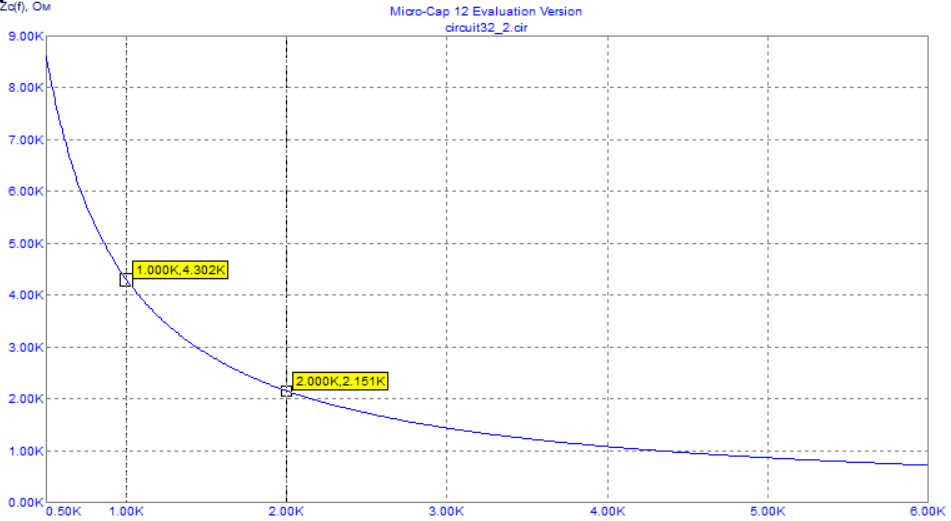 Рис. 13 – График зависимости модуля комплексного сопротивления конденсатора от частоты Полученные данные величин модуля комплексного сопротивления конденсатора на частотах f = 1, 2, 3, 4, 5 кГц занесены в таблицу 1. 4.1.2. Построение зависимости фазы сопротивления С-цепи от частоты. В окне AC Analysis Limits устанавливаем параметры Y Expression - “ph(V(C1)/I(C1))” и Y Range – “0, -180, 30” (рис.14). 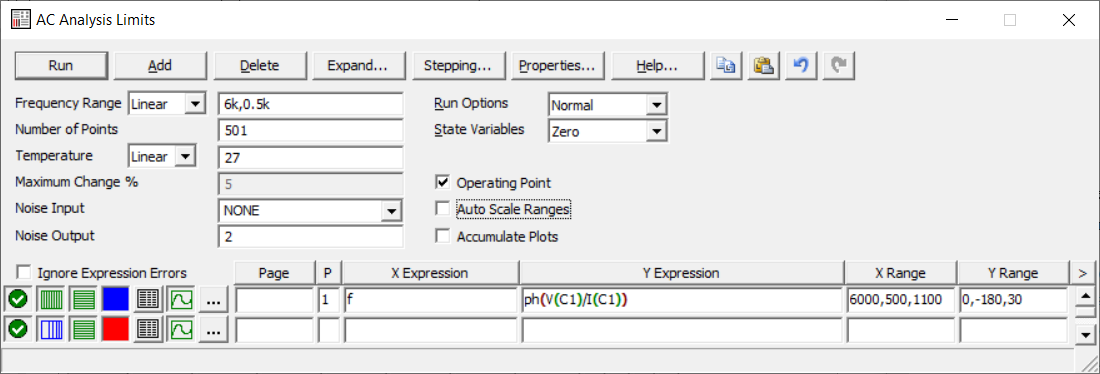 Рис. 14 Получили график как на рисунке 15. На графике отмечены величины фазы комплексного сопротивления конденсатора при f = 1 кГц и f = 2 кГц. 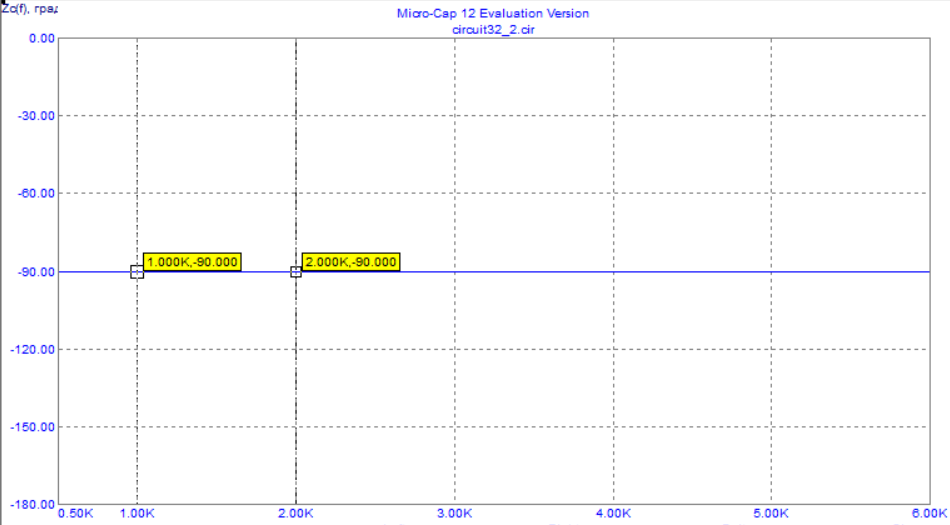 Рис.15 - Зависимость фазы комплексного сопротивления конденсатора от частоты С помощью окна Go To X задаем значения частоты f = 1, 2, 3, 4, 5 кГц и заполняем таблицу 1. 4.2. Исследование модуля и фазы комплексного сопротивления RС-цепи.Добавляем в предыдущую схему резистор (рис. 16). 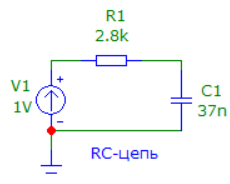 Рис.16 Построение зависимости модуля и фазы комплексного сопротивления RC-цепи от частоты. В окне AC Analysis Limits устанавливаем параметры как на рис.17. 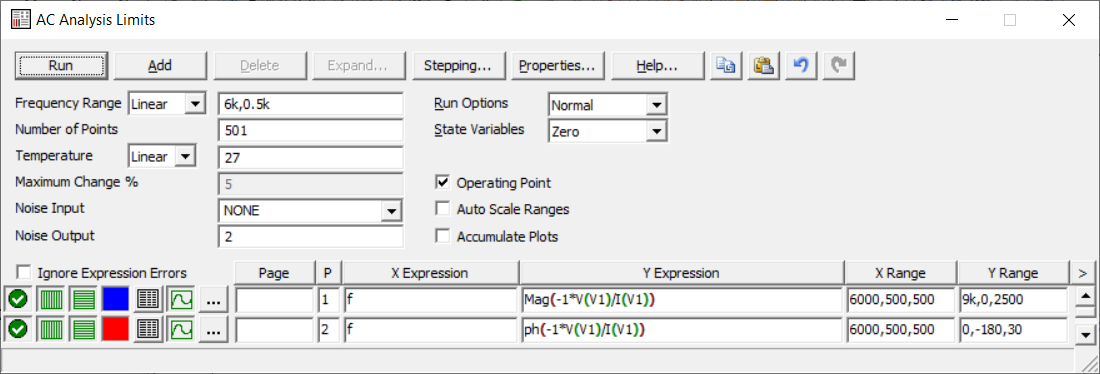 Рис. 17 Получили графики (рис.18). 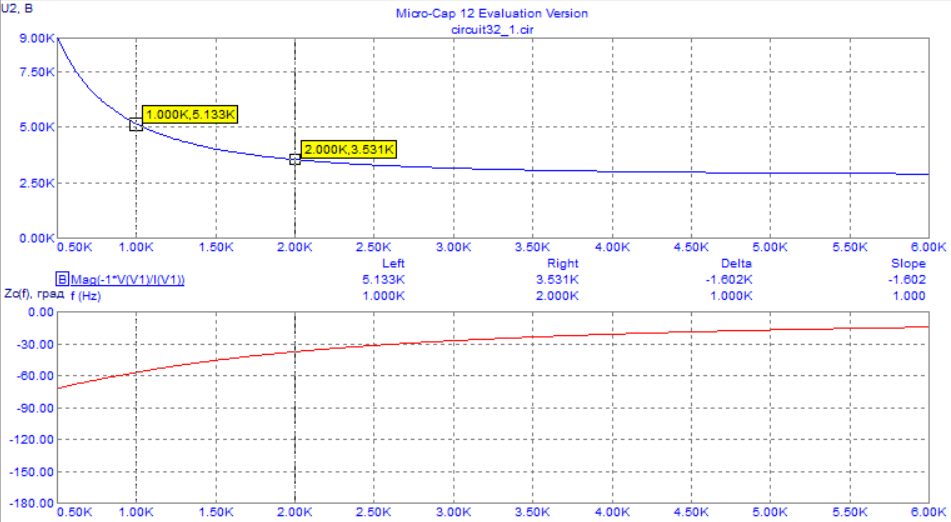 Рис. 18 - Зависимости модуля и фазы комплексного сопротивления RC-цепи от частоты С помощью окна Go To X задаем значения частоты f = 1, 2, 3, 4, 5 кГц и заполняем таблицу 2. 4.3. Исследование модуля и фазы комплексного напряжения на конденсаторе RC-цепи.В окне AC Analysis Limits устанавливаем следующие параметры (рис.19). 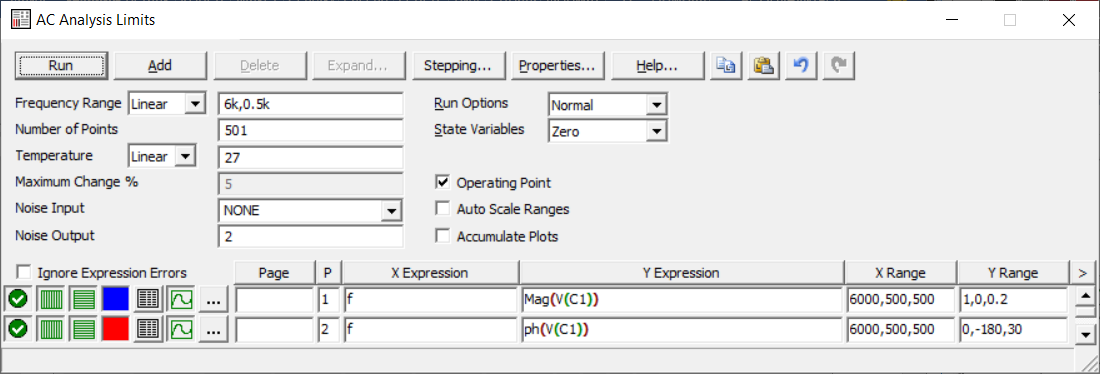 Рис. 19 Получили графики (рис.20). 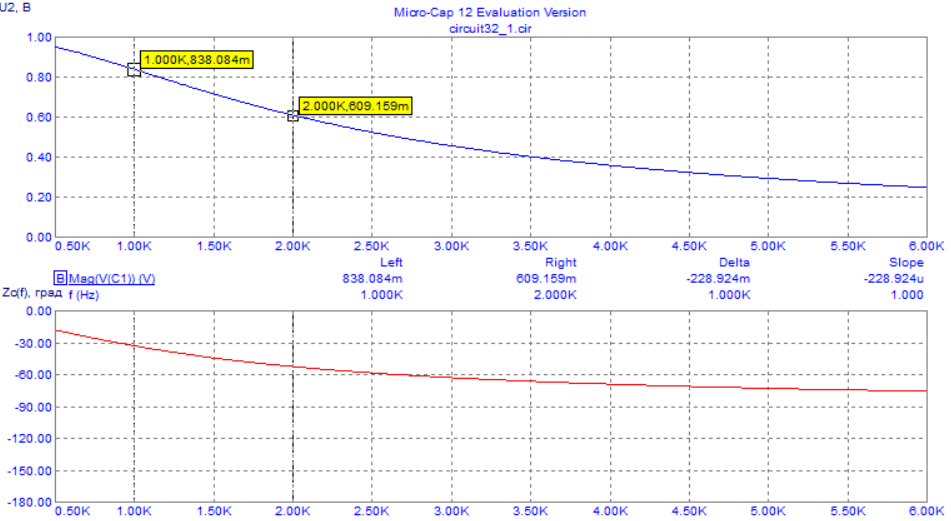 Рис. 20 – Зависимость модуля и фазы комплексного напряжения на конденсаторе 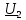 в RC-цепи от частоты в RC-цепи от частоты С помощью окна Go To X задаем значения частоты f = 1, 2, 3, 4, 5 кГц и заполняем таблицу 3. 4.4. Исследование модуля и фазы комплексного сопротивления L-цепи.Собираем схему с источником синусоидального напряжения и катушкой (рис.21). 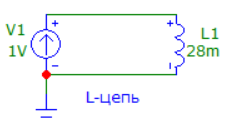 Рис. 21 – Схема для исследования модуля и фазы комплексного сопротивления L-цепи Построение зависимости модуля и фазы комплексного сопротивления L-цепи от частоты. В меню Analysis выбрали команду AC…. В окне AC Analysis Limits устанавливаем параметры (рис.22). 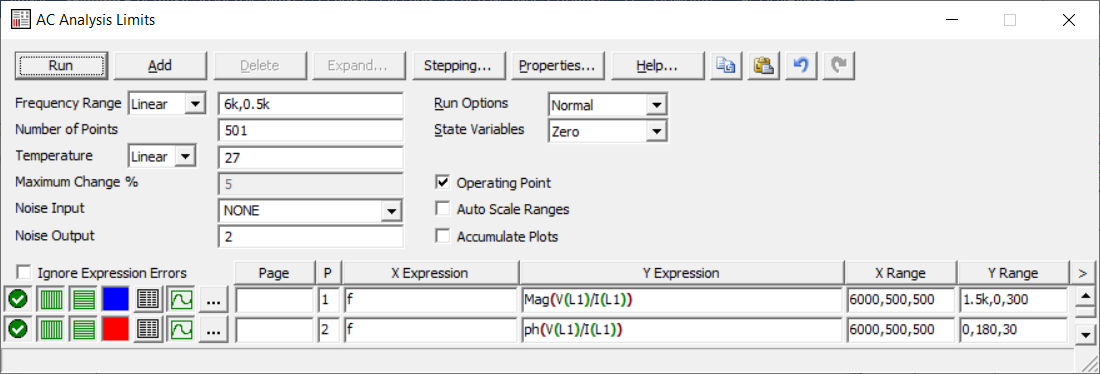 Рис. 22 Получили графики (рис.23). 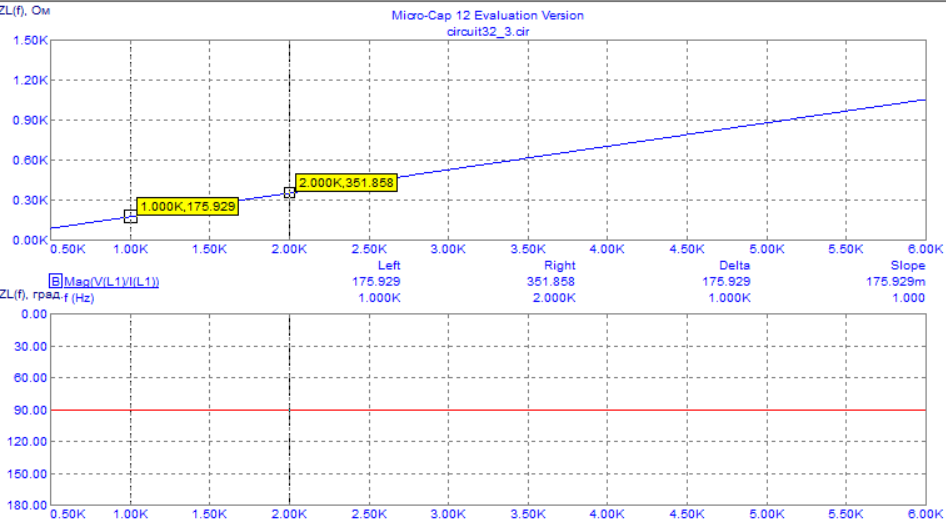 Рис. 23 – Зависимости модуля и фазы комплексного сопротивления катушки от частоты С помощью окна Go To X задаем значения частоты f = 1, 2, 3, 4, 5 кГц и заполняем таблицу 4. 4.5. Исследование модуля и фазы комплексного сопротивления RL-цепи.Добавляем в предыдущую схему резистор R1 = 2.8k (рис. 24). 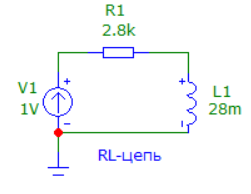 Рис.24 Построение зависимости модуля и фазы комплексного сопротивления RL-цепи от частоты. В окне AC Analysis Limits устанавливаем параметры как на рис.25. 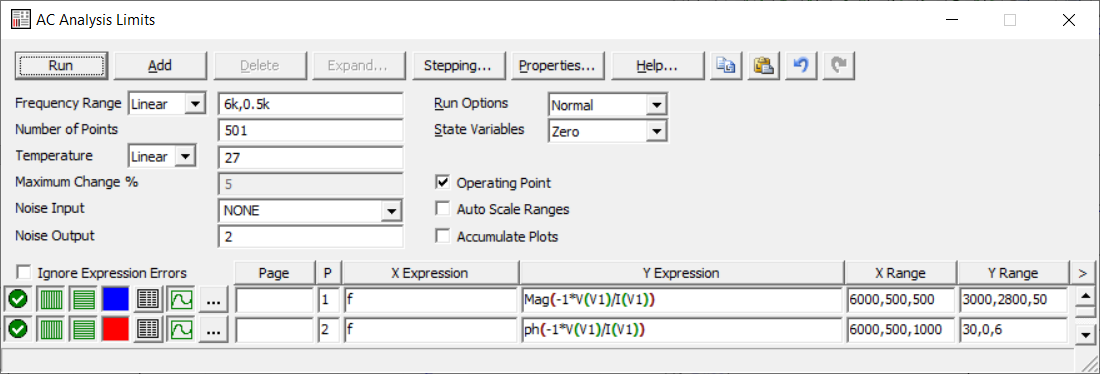 Рис. 25 Получили графики (рис.26). 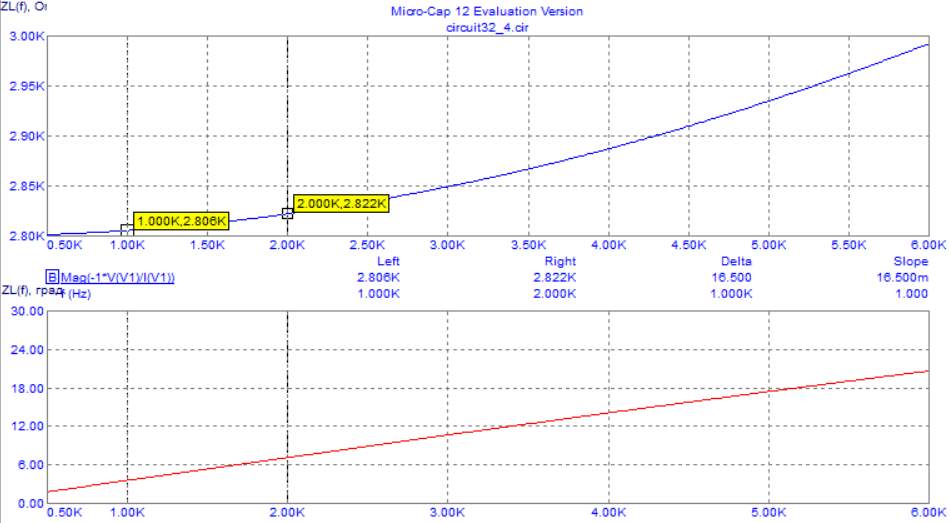 Рис. 26 - Зависимости модуля и фазы комплексного сопротивления RL-цепи от частоты С помощью окна Go To X задаем значения частоты f = 1, 2, 3, 4, 5 кГц и заполняем таблицу 5. 4.6. Исследование модуля и фазы комплексного напряжения на катушке RL-цепи.В окне AC Analysis Limits устанавливаем следующие параметры (рис.27). 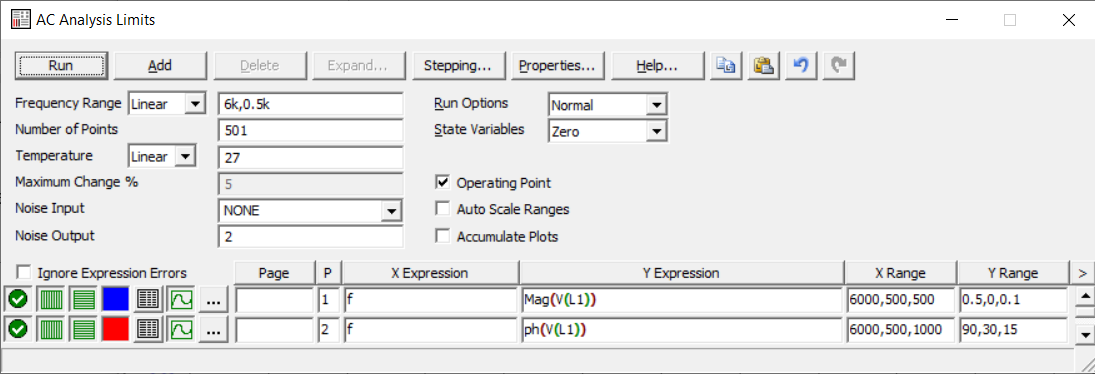 Рис. 27 Получили графики (рис.28). 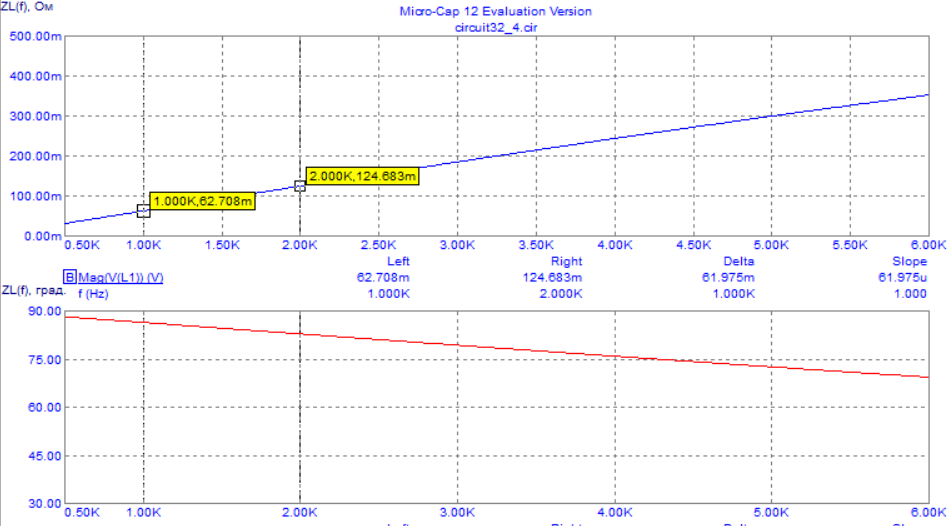 Рис. 28 – Зависимость модуля и фазы комплексного напряжения на конденсаторе 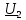 в RL-цепи от частоты в RL-цепи от частоты С помощью окна Go To X задаем значения частоты f = 1, 2, 3, 4, 5 кГц и заполняем таблицу 6. Выводы.В ходе проделанной работы были исследованы электрический режим конденсатора и катушки индуктивности в цепях гармонического тока. Было рассчитано комплексное сопротивление конденсатора для различных частот, определены его модуль и аргумент, построена векторная диаграмма. При исследовании модуля и фазы комплексного сопротивления С-цепи в программе Micro-Cap, были получены параметры, полностью совпадающие с величинами предварительного расчета. Произведён расчет комплексного сопротивления RC-цепи для различных частот, определено его полное сопротивление и аргумент, построена векторная диаграмма. При исследовании модуля и фазы комплексного сопротивления RС-цепи в программе Micro-Cap, были получены параметры, полностью совпадающие с величинами предварительного расчета. Произведён расчет напряжения на конденсаторе RC-цепи для различных частот, напряжение записано в экспоненциальной форме. При исследовании модуля и фазы комплексного напряжения на конденсаторе RС-цепи в программе Micro-Cap, были получены параметры, полностью совпадающие с величинами предварительного расчета. Произведён расчет комплексного сопротивления катушки индуктивности для различных частот, определено ее полное сопротивление и аргумент, построена векторная диаграмма. При исследовании модуля и фазы комплексного сопротивления L-цепи в программе Micro-Cap, были получены параметры, полностью совпадающие с величинами предварительного расчета. Произведён расчет комплексного сопротивления RL-цепи для различных частот, определено его полное сопротивление и аргумент, построена векторная диаграмма. При исследовании модуля и фазы комплексного сопротивления RL-цепи в программе Micro-Cap, были получены параметры, полностью совпадающие с величинами предварительного расчета. Произведён расчет напряжения на катушке индуктивности RL-цепи для различных частот, напряжение записано в экспоненциальной форме. При исследовании модуля и фазы комплексного напряжения на катушке RL-цепи в программе Micro-Cap, были получены параметры, полностью совпадающие с величинами предварительного расчета. Вопросы для самопроверкиКакая частота называется граничной для RL-цепи? Граничной называется частота, при которой модуль реактивного сопротивления равен резистивному сопротивлению. 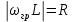 , , 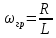 , , 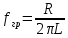 . .Каково значение модуля входного сопротивления RL-цепи на граничной частоте? На граничной частоте модуль входного сопротивления RL-цепи: 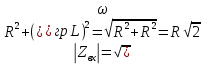 . .Каково значение аргумента входного сопротивления RL-цепи на граничной частоте? 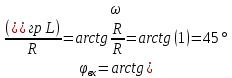 . .К чему стремится модуль тока RL-цепи при увеличении частоты? При увеличении частоты увеличится индуктивное сопротивление, соответственно увеличится модуль входного сопротивления. Модуль тока RL-цепи будет уменьшаться и стремится к 0. Чему равен модуль входного сопротивления RL-цепи при частоте равной нулю? При частоте равной нулю модуль входного сопротивления RL-цепи равен R. Москва 2021 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

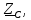 Ом
Ом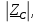 Ом
Ом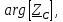 град.
град.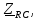 Ом
Ом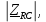 Ом
Ом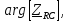 град.
град.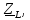 Ом
Ом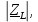 Ом
Ом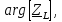 град.
град.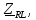 Ом
Ом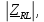 Ом
Ом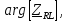 град.
град.