Изменение световой волны. №4 Измерение длины световой волны с помощью прозрачной дифракцио. Лабораторная работа 4 Измерение длины световой волны с помощью прозрачной дифракционной решетки

• Название: Лабораторная работа 4 Измерение длины световой волны с помощью прозрачной дифракционной решетки
• Анкор: Изменение световой волны
• Дата: 01.10.2022
• Размер: 63.46 Kb.
• Имя файла: №4 Измерение длины световой волны с помощью прозрачной дифракцио.docx
• Тип: Лабораторная работа; #708758

Лабораторный вариант 02.02.2022

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Санкт-Петербургский горный университет»

Кафедра общей и технической физики

общая физика

Лабораторная работа №4

Измерение ДЛИНЫ СВЕТОВОЙ ВОЛНЫ

С ПОМОЩЬЮ ПРОЗРАЧНОЙ

ДИФРАКЦИОННОЙ РЕШЕТКИ

Методические указания к лабораторной работе

САНКТ-ПЕТЕРБУРГ 2022

Определение ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ

ПРОЗРАЧНОЙ ДИФРАКЦИОННОЙ РЕШЕТКИ
Теоретические сведения

Дифракционная решетка – это прозрачная пластина с нанесенными на нее непрозрачными штрихами равной ширины b (рис.1). Между непрозрачными штрихами имеются прозрачные одинаковые щели шириной a.


С 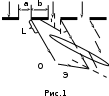умма a + b = d называется постоянной (периодом) дифракционной решетки.

При прохождении света через любую из щелей происходит дифракция, в результате которой волны распространяются от щели по всем направлениям. Идущие от всех щелей волны собираются линзой О на экране Э и интерферируют между собой. В конкретную точку экрана попадают волны, идущие только под определенным углом  по отношению к дифракционной решетке.

Таким образом, дифракционная решетка осуществляет наложение двух процессов: дифракции на каждой отдельной щели и интерференции излучения от всех щелей.

Значительное усиление волн будет происходить только под теми углами , для которых световые волны, идущие от всех щелей, усиливают друг друга. Это взаимное усиление будет осуществляться, если оптическая разность хода лучей от соседних щелей L кратна длине световой волны. Из рис.1 видно, что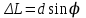

.

Таким образом, взаимное усиление волн будет происходить только под некоторыми углами , подчиняющимися условию максимумов интенсивности света, прошедшего дифракционную решетку: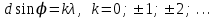

,

где  – длина волны, k порядок дифракции. При k = 0(нулевой порядок дифракции) все длины волн после прохождения через дифракционную решетку распространяются под одним и тем же углом  = 0 и собираются в центре экрана. Если цвет излучения, падающего на решетку, белый, то и цвет яркой полоски в центре экрана также будет белым.

Если k = +1 (первый правый порядок дифракции), то для каждой длины волны найдется свой угол  максимального усиления, т.е. на экране будут видны отдельные цветные полоски, каждая из которых соответствует определенной длине волны.

Таким образом, дифракционная решетка осуществляет разложение световой волны по длинам волн (спектральное разложение). Аналогичная ситуация будет наблюдаться при k = 1 (первый левый порядок дифракции). Цветные полоски (спектральные линии) в этом случае лежат слева от нулевого порядка.

Спектральные линии будут наблюдаться также во втором правом и втором левом порядках (k = +2 и k = 2) и т.д.

Свойство дифракционной решетки – давать максимумы для разных длин волн под разными углами  – используется для измерения длины волны оптического излучения.

Спектр излучения, используемой в лабораторной работе ртутной лампы содержит четыре достаточно интенсивных спектральных линии, различающихся цветом.

Нулевой порядок дифракции (k = 0) легко распознается, так как соответствующая линия имеет такой же цвет, как цвет излучения ртутной лампы и яркость ее значительно больше остальных линий. Справа и слева симметрично от нулевого порядка можно наблюдать цветные линии. Наиболее близко к линии нулевого порядка (справа и слева) располагаются фиолетовые линии, на большем расстоянии зеленые, желтые и красные. Все эти линии, расположенные наиболее близко к линии нулевого порядка, образуют дифракционный спектр первого порядка (для линий справа k = +1; слева k = –1). Далее следуют спектры второго (k = +2 и k = –2) и третьего порядков. Интенсивность наблюдаемых спектральных линий уменьшается с ростом порядка дифракции.
Описание экспериментальной установки

Источником оптического излучения с линейчатым спектром служит ртутная лампа 1 (рис.2). Коллиматор 2 (собирающая линза установлена на фокусном расстоянии от входной щели S) формирует параллельный пучок света, который падает на дифракционную решетку 3.

Д 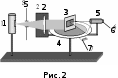ифракционная решетка установлена на столике гониометра 4, так что ее штрихи расположены вертикально, а плоскость перпендикулярна оси коллиматора. Излучение, прошедшее дифракционную ре­шетку, попадает в зрительную трубу 5, имеющую визир в фокальной плоскости окуляра 6. Наблюдая в окуляр спектральную линию, совмещают ее с визиром, поворачивая для этого подвижную часть столика вместе с укрепленной на ней зрительной трубой. Измерение углов дифракции производится по лимбу 7 гониометра.
Порядок выполнения работы

1. Включить ртутную лампу, переведя тумблер на блоке питания в положение «Вкл» и убедиться, что входная щель ярко освещена. При этом в окуляр должна наблюдаться симметричная картина спектральных линий, и в середине – нулевой порядок дифракции.

2 . Сфокусировать окуляр так, чтобы изображения спектральных линий и визира были четкими. Для повышения точности измерений установить ширину входной щели такой, чтобы линии были узкими, но при этом достаточно интенсивными.

3. Повернув подвижную часть столика со зрительной трубой, совместить визир с заданной преподавателем спектральной линией в первом порядке дифракции справа и определить значение угла по круговой шкале гониометра с помощью нониуса (рис.3). Затем проделать то же самое, настроив зрительную трубу на ту же линию в первом порядке слева. Измерения угла  повторить три раза.

4. Провести аналогичные измерения для видимых глазом линий во втором и третьем порядках и записать результаты.

5. Выключить ртутную лампу, переведя тумблер на блоке питания в положение «Выкл».

6. Вычислить удвоенный угол дифракции 2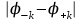  = для всех измерений в каждом порядке.

7. Определив значение угла дифракции , для каждой спектральной линии в отдельности, рассчитать sin  и .

8. Рассчитать период дифракционной решетки, как d=1/N. Значение N указано на дифракционной решетке.

9. Определить значения  спектральных линий излучения ртути (по указанию преподавателя). Рассчитать среднее значение .

Выразить окончательные значения средних длин волн в нанометрах и сравнить их с табличными значениями. Определить погрешность измерения длины волны.

Результаты измерений записать в таблицу:

цвет спектральной линии	K (порядок)	Номер измерения	–k	k	2	(2)		sin 	
			град.	град.	град.	град.	град.		мм
фиолетовый	1	1
		2
		3
										ср=
	2	1
		2
		3
										ср=
	3	1
		2
		3
										ср=

цвет спектральной линии	K (порядок)	Номер измерения	–k	k	2	(2)		sin 	
зеленый	1	1
		2
		3
									ср=
	2	1
		2
		3
									ср=
	3	1
		2
		3
									ср=

цвет спектральной линии	K (порядок)	Номер измерения	–k	k	2	(2)		sin 	
желтый	1	1
		2
		3
									ср=
	2	1
		2
		3
									ср=
	3	1
		2
		3
									ср=

Контрольные вопросы

1. Дайте определение дифракции света.

2. Сформулируйте принцип Гюйгенса – Френеля.

3. Какое устройство называют дифракционной решеткой? Запишите формулу дифракционной решетки.

4. Как определить период дифракционной решетки?

5. Чем отличаются дифракционные решетки, работающие в инфракрасной и видимой областях спектра?

6. Почему дифракционный максимум нулевого порядка белого света не окрашен, а максимумы других порядков окрашены?

7. Условия максимумов для дифракционной решетки аналогично условию минимумов для одной щели. Как объяснить это кажущееся противоречие?

8. Какую величину называют разрешающей способностью дифракционной решетки?

9. Каким условием определяется наибольший порядок спектра решетки?

Требования к содержанию отчёта по лабораторной работе

Отчёт оформляется в печатном виде на листах формата А4 в соответствии с указанными ниже требованиями.

Помимо стандартного титульного листа в содержании отчёта должны быть раскрыты пункты, перечисленные ниже.

1. Цель работы.

2. Краткое теоретическое содержание.

1) Явление, изучаемое в работе.

2) Определения основных физических понятий, объектов, процессов и величин.

3) Законы и соотношения, описывающие изучаемые процессы, на основании которых, получены расчётные формулы.

4) Пояснения к физическим величинам и их единицы измерений.

3. Схема установки.

4. Расчётные формулы.

5. Формулы для расчёта погрешностей косвенных измерений.

6. Таблицы с результатами измерений и вычислений. (Таблицы должны иметь номер и название. Единицы измерения физических величин должны быть указаны в отдельной строке таблицы под строкой с обозначениями физических величин.)

7. Пример вычисления (для одного опыта).

1) Исходные данные.

2) Вычисления.

3) Окончательный результат.

8. Графический материал.

1) Записать аналитическое выражение функциональной зависимости, которая представлена на графике.

2) На осях координат указать масштаб, физические величины и единицы измерения.

3) На координатной плоскости должны быть нанесены экспериментальные точки.

4) По результатам эксперимента, представленным на координатной плоскости, провести плавную линию, аппроксимирующую функциональную теоретическую зависимость в соответствии с методом наименьших квадратов.

9. Анализ полученного результата. Выводы.

РЕКОМЕНДАЦИИ ПО ЗАЩИТЕ ОТЧЕТА

К защите допускаются студенты, подготовившие отчет в соответствии с требованиями к его содержанию в установленные сроки. После проверки преподавателем содержания отчёта, при наличии ошибок и недочетов, работа возвращается студенту на доработку. При правильном выполнении лабораторной работы, соблюдении всех требований к содержанию и оформлению отчёта, студент допускается к защите.

Для успешной защиты отчета необходимо изучить теоретический материал по теме работы, а так же освоить математический аппарат, необходимый для вывода расчётных формул работы.

При подготовке к защите, помимо данного методического пособия, необходимо использовать учебники и другие учебные пособия, рекомендованные к учебному процессу кафедрой ОТФ.

Во время защиты студент должен уметь ответить на вопросы преподавателя в полном объёме теоретического и методического содержания данной лабораторной работы, уметь самостоятельно вывести необходимые расчётные формулы, выполнить анализ полученных зависимостей и прокомментировать полученные результаты.