ТСП_ЛБ4_0В92_Макаревич. Лабораторная работа 4 Опционы Вариант 8 студент гр. 0В92 Макаревич Д. В. Проверил
 Скачать 2.72 Mb.
|
 Инженерная школа ядерных технологий Направление 01.03.02 «Прикладная математика и информатика» Лабораторная работа №4 Опционы Вариант - 8 Выполнил: студент гр. 0В92 _____________ Макаревич Д.В. Проверил: преподаватель _____________ Бельснер О.А. Томск – 2022 ХОД РАБОТЫ Задание: В условиях лабораторной работы №3 и пользуясь формулой Блэка-Шоулса, найти справедливую цену опциона покупателя (нечетные варианты) или продавца (четные варианты) европейского типа в момент времени (T-t)=3 года (узел 250, шаг по времени равен 0,004 года, интервал времени есть [0,4]) при цене исполнения E=8S0/7 (нечетные варианты) или E=7S0/8 (четные варианты). Безрисковую процентную ставку положить r=0.1. Данные по ценам базового актива взять из решения, найденного в лаб.3, п.3, по волатильностям – по номеру своего задания (не забудьте перевести волатильность в исходном задании в доли) Вычислить долю хеджируемого капитала для опциона покупателя европейского типа  (для нечетных вариантов) и минимальную доходность риск-нейтрального портфеля  (для четных вариантов, P – справедливая цена опциона продавца европейского типа) в моменты времени  , начиная с нулевого, с шагом 0,5 года. Пусть T=1 год. Используя файл дополнительных недельных данных котировок (приложение 1) и перейдя к относительным доходностям цен акций, вычислите годовую реализованную волатильность σ приращений, применяя формулу несмещенной оценки дисперсии. Рассмотрите опцион покупателя европейского типа со страйком 50 у.е., безрисковой процентной ставкой r=0.10, ценами Sj (приложение 1) и вычисленной волатильностью σ, а также временем до исполнения τ=(T-tj) =  долей временного интервала [0,1],  . Используя функции MathCad pnorm() и dnorm(), вычислите и постройте графики для «греческих»  ,  ,  в произвольный момент времени τ до исполнения контракта, беря за начальную точку отсчета S0. Стремится ли значение к нулю в момент исполнения τ=0?
Задание 1. 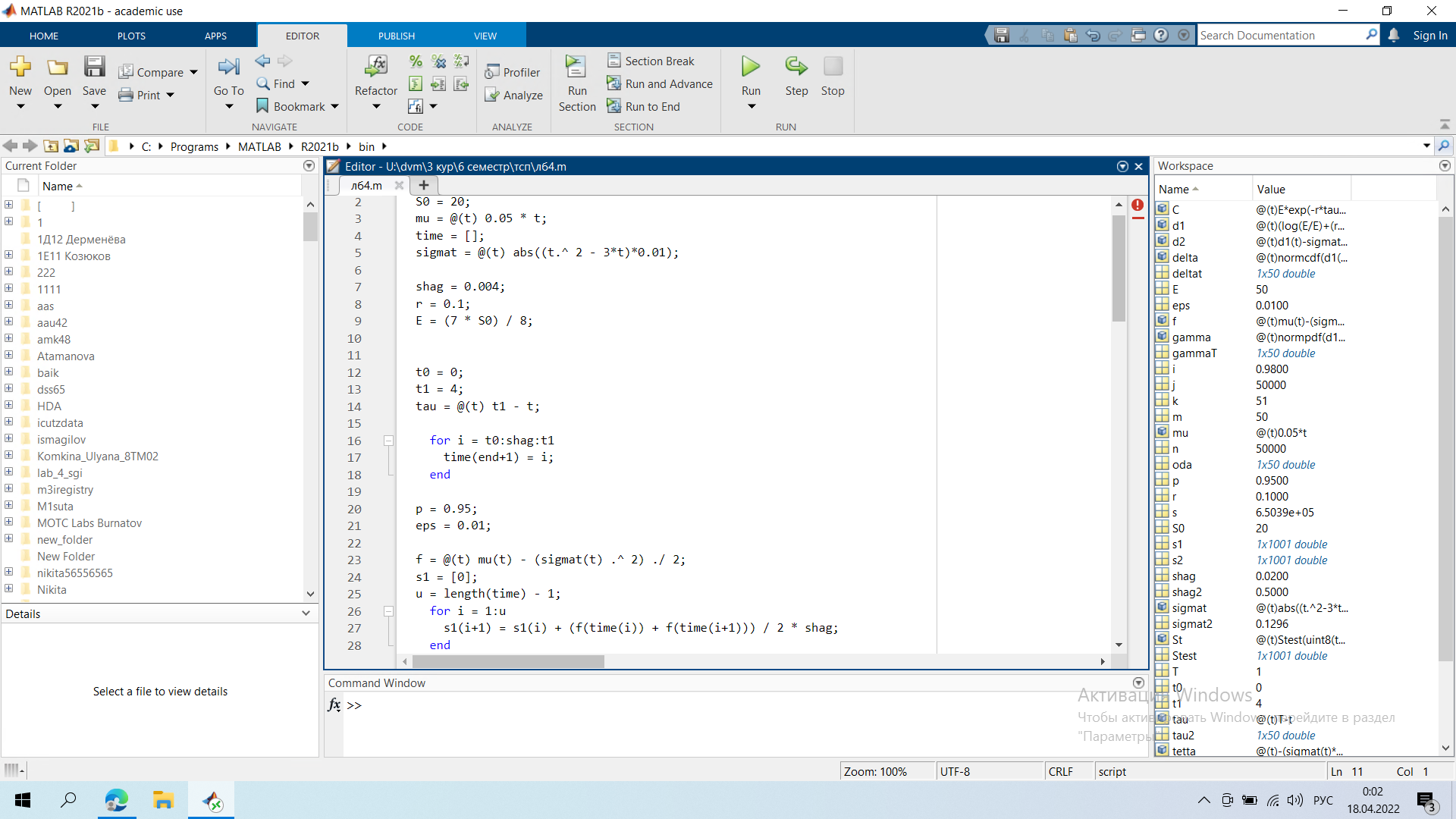 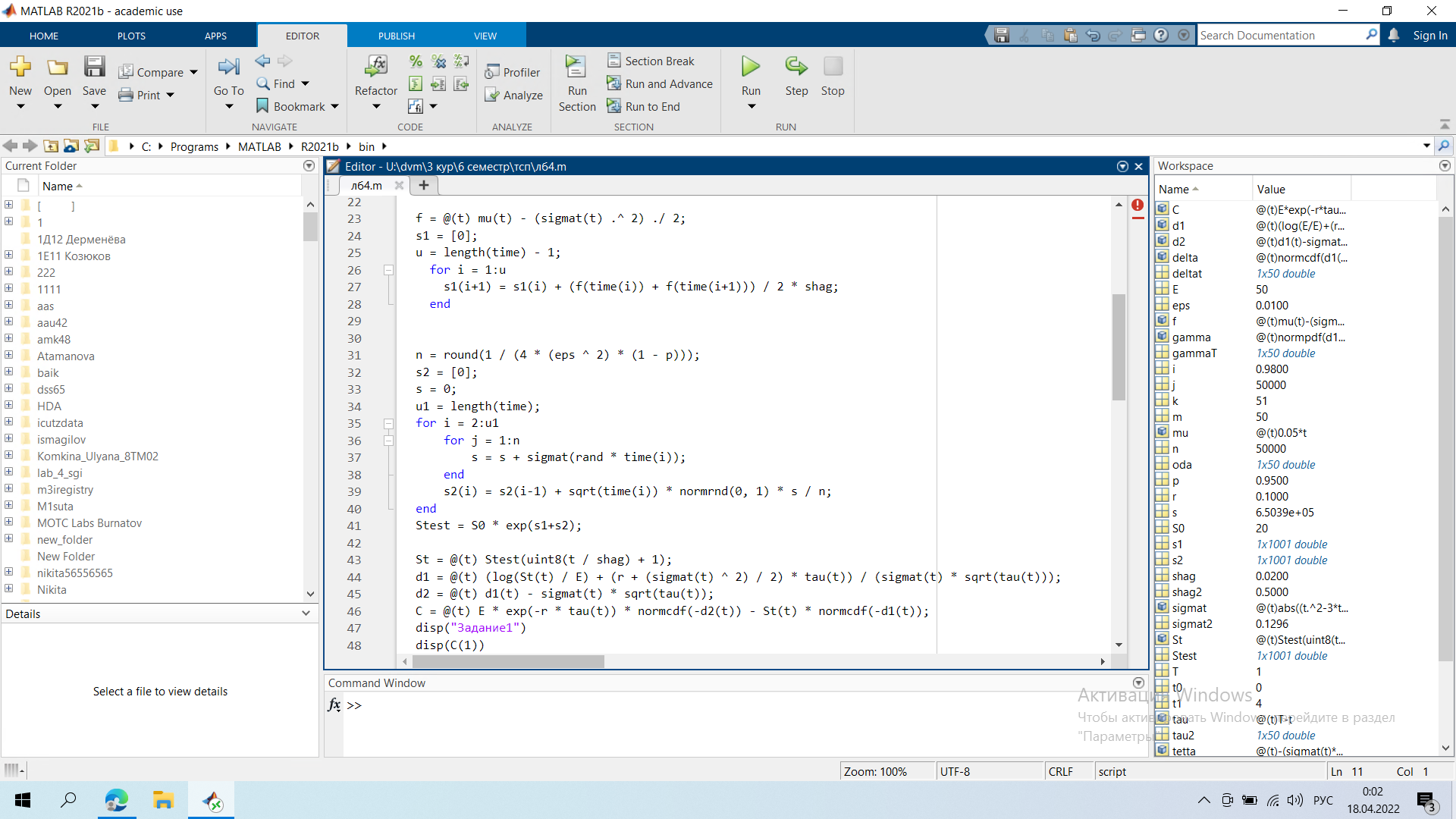 Справедливая цена опциона в момент времени t=1 = 11,67 Задание 2 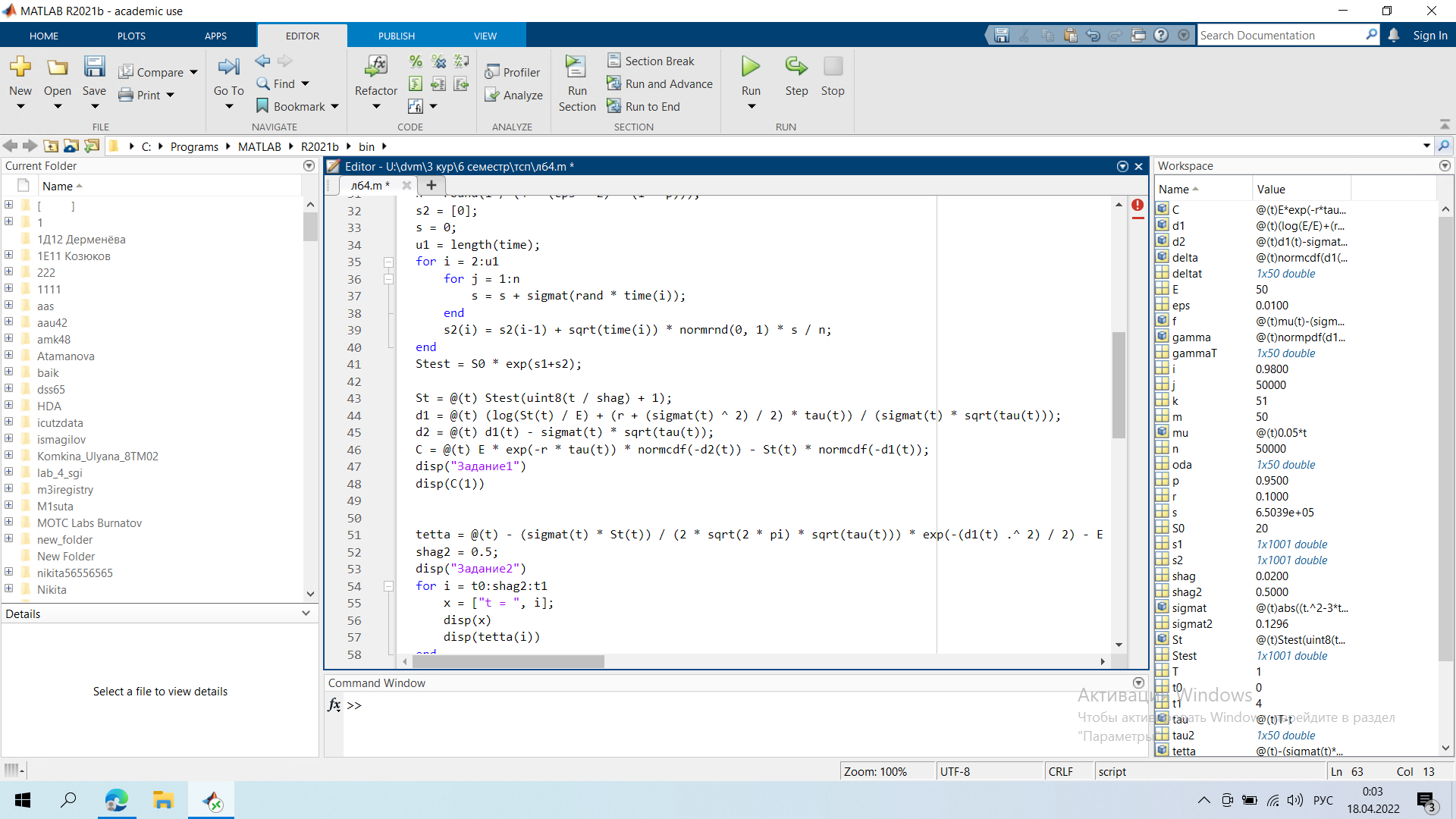 Минимальные доходности в конце на общем скриншоте Задание 3. 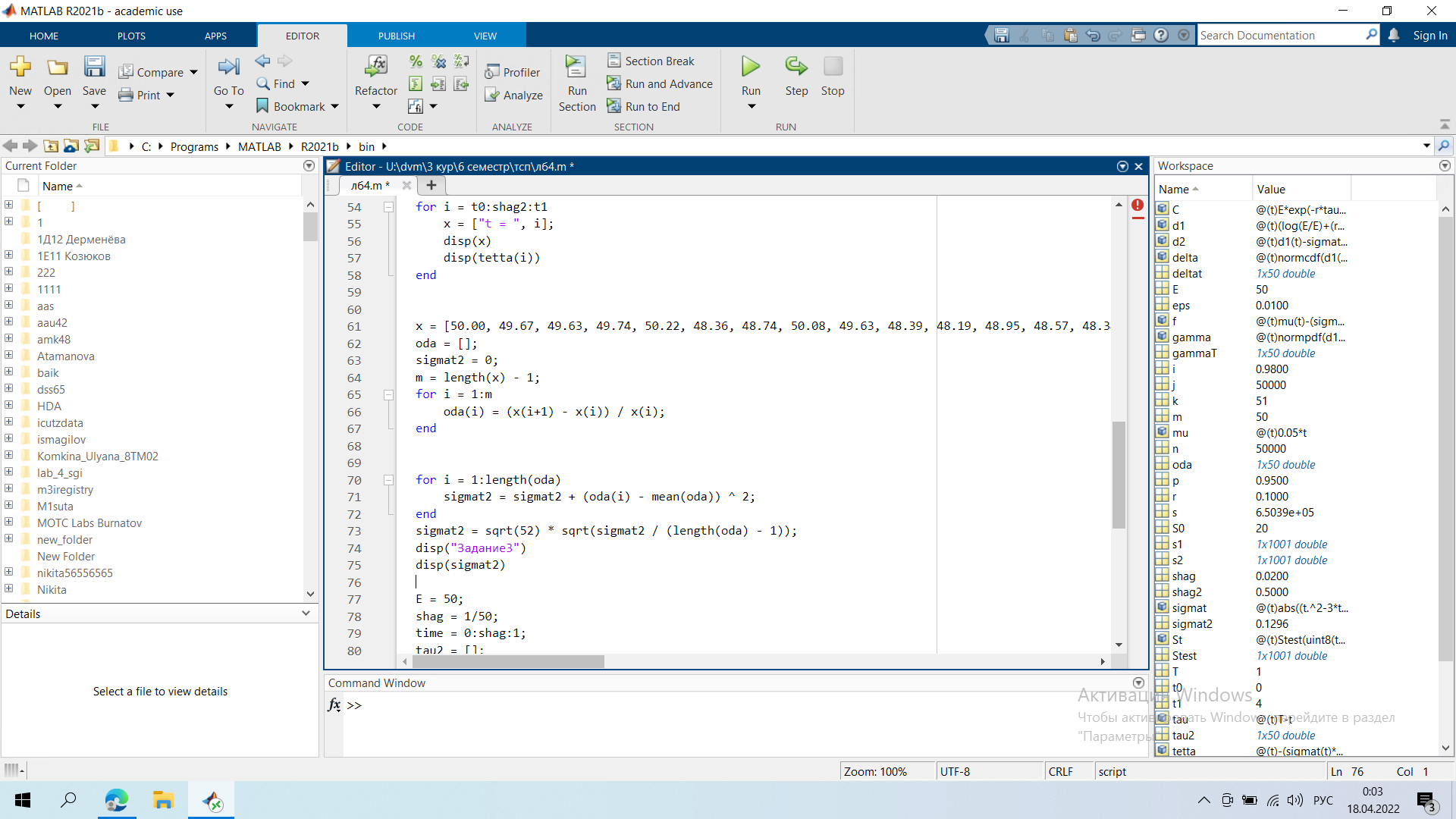 Годовая реализованная волатильность σ - приращений = 0,1296 Задание 4. 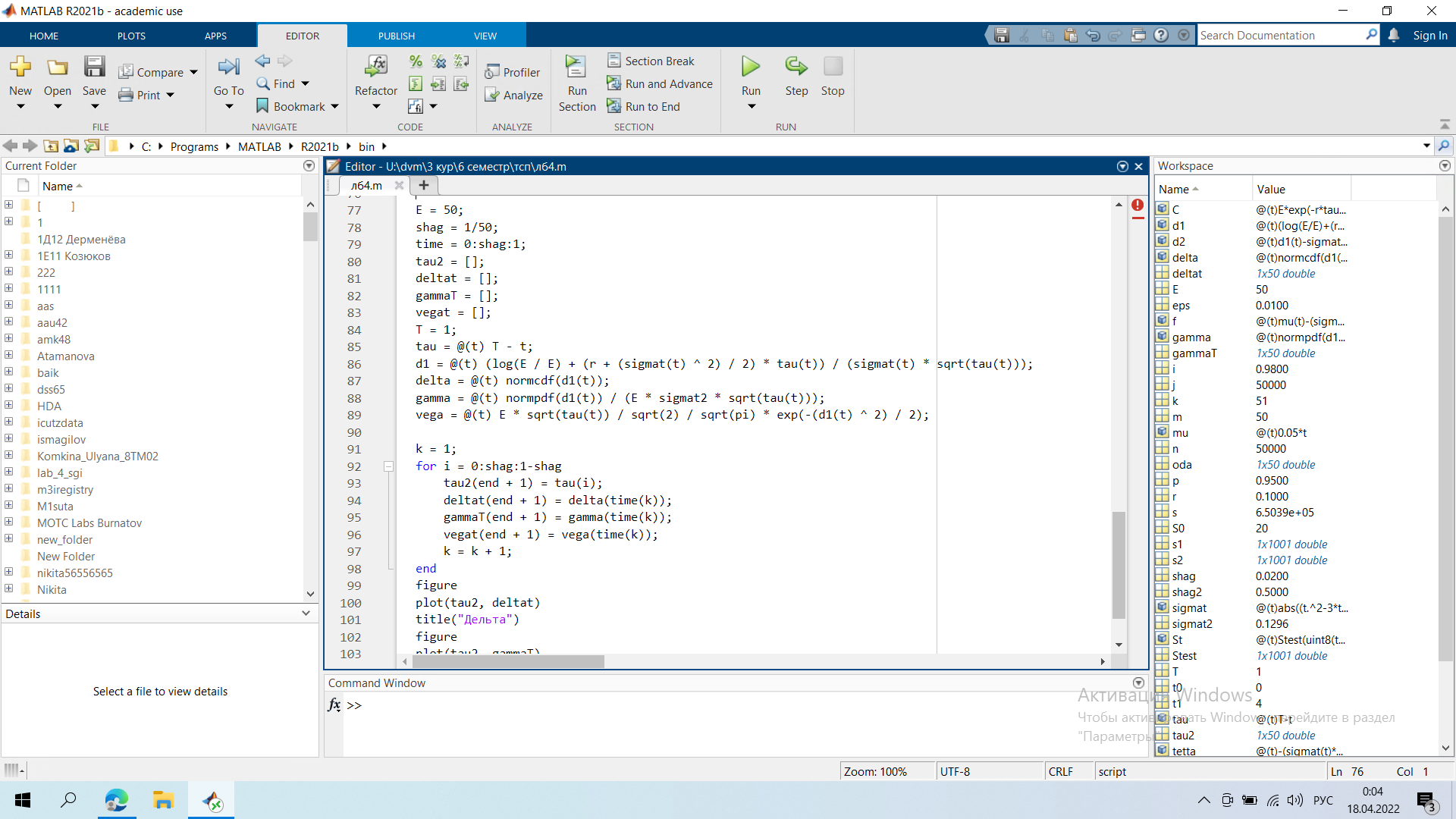 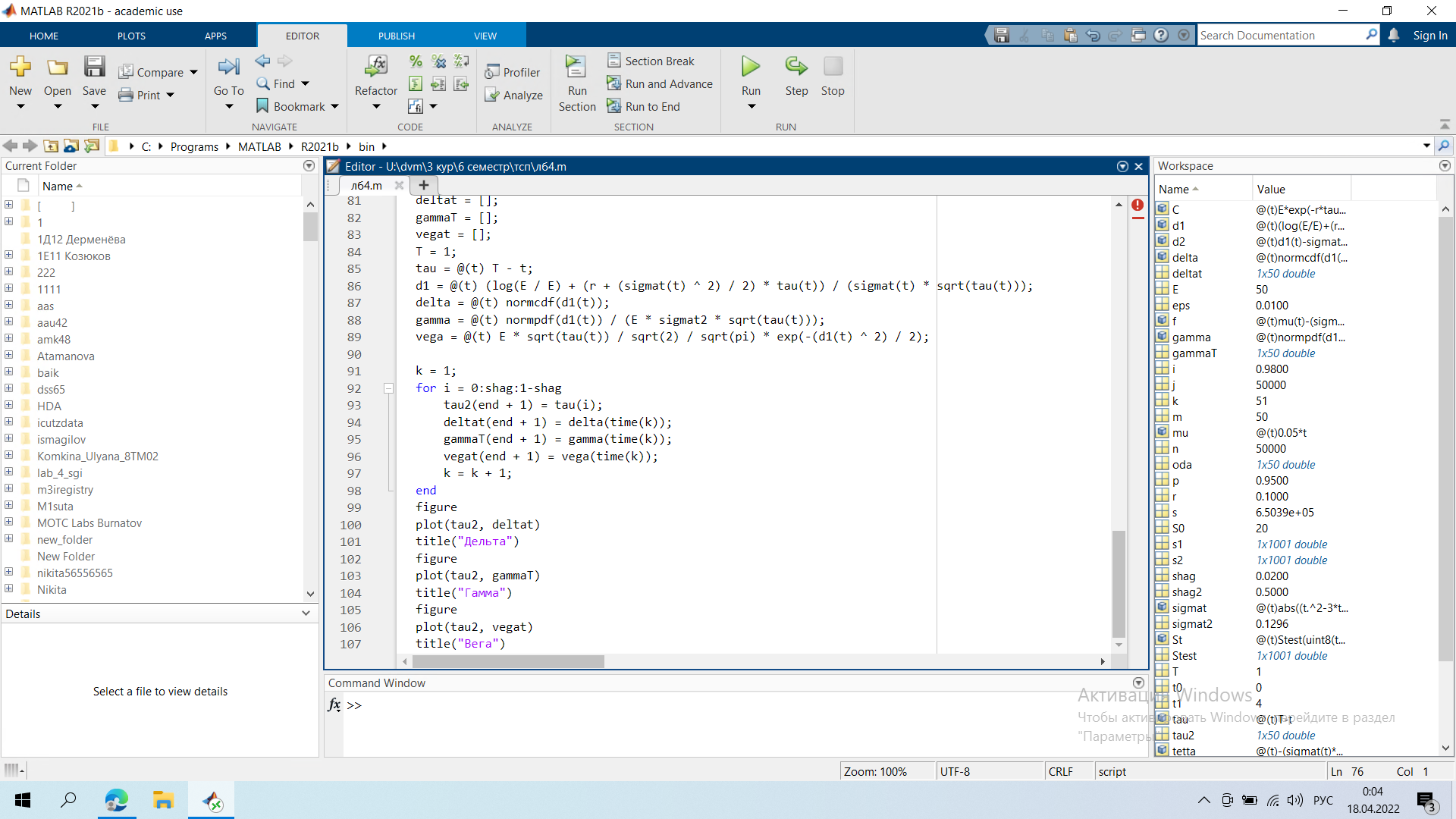 Графики все внизу Результаты: 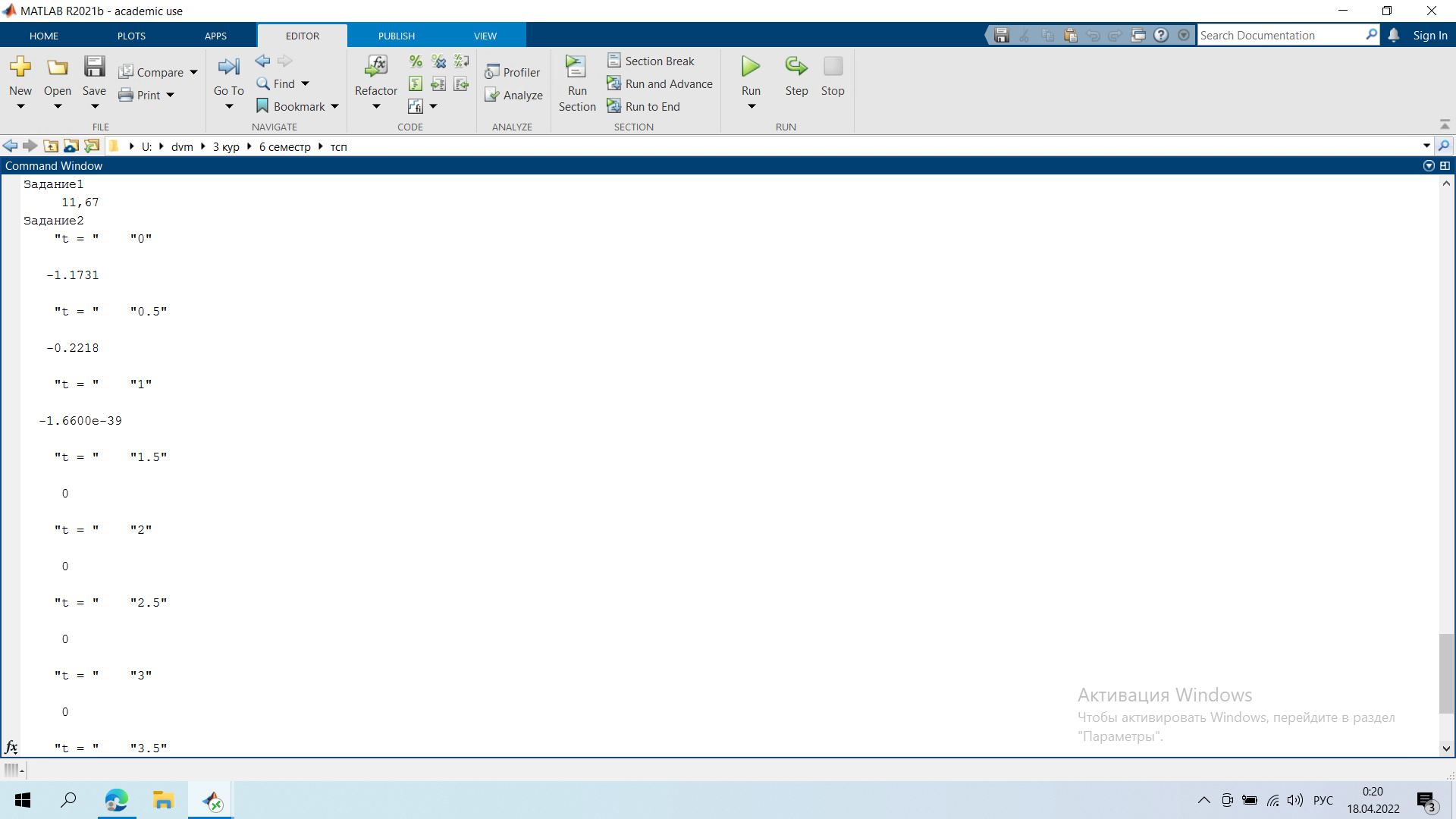 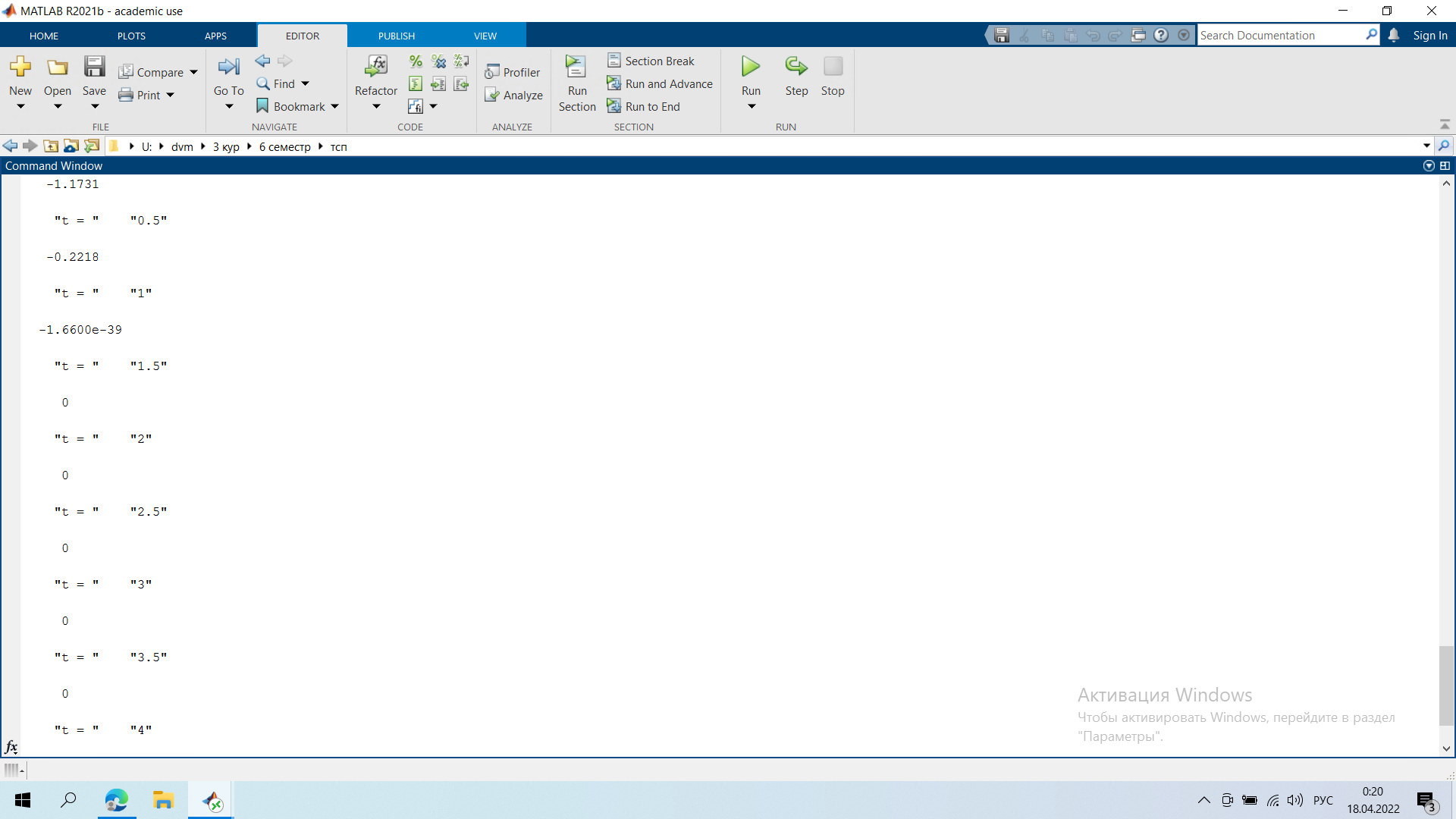 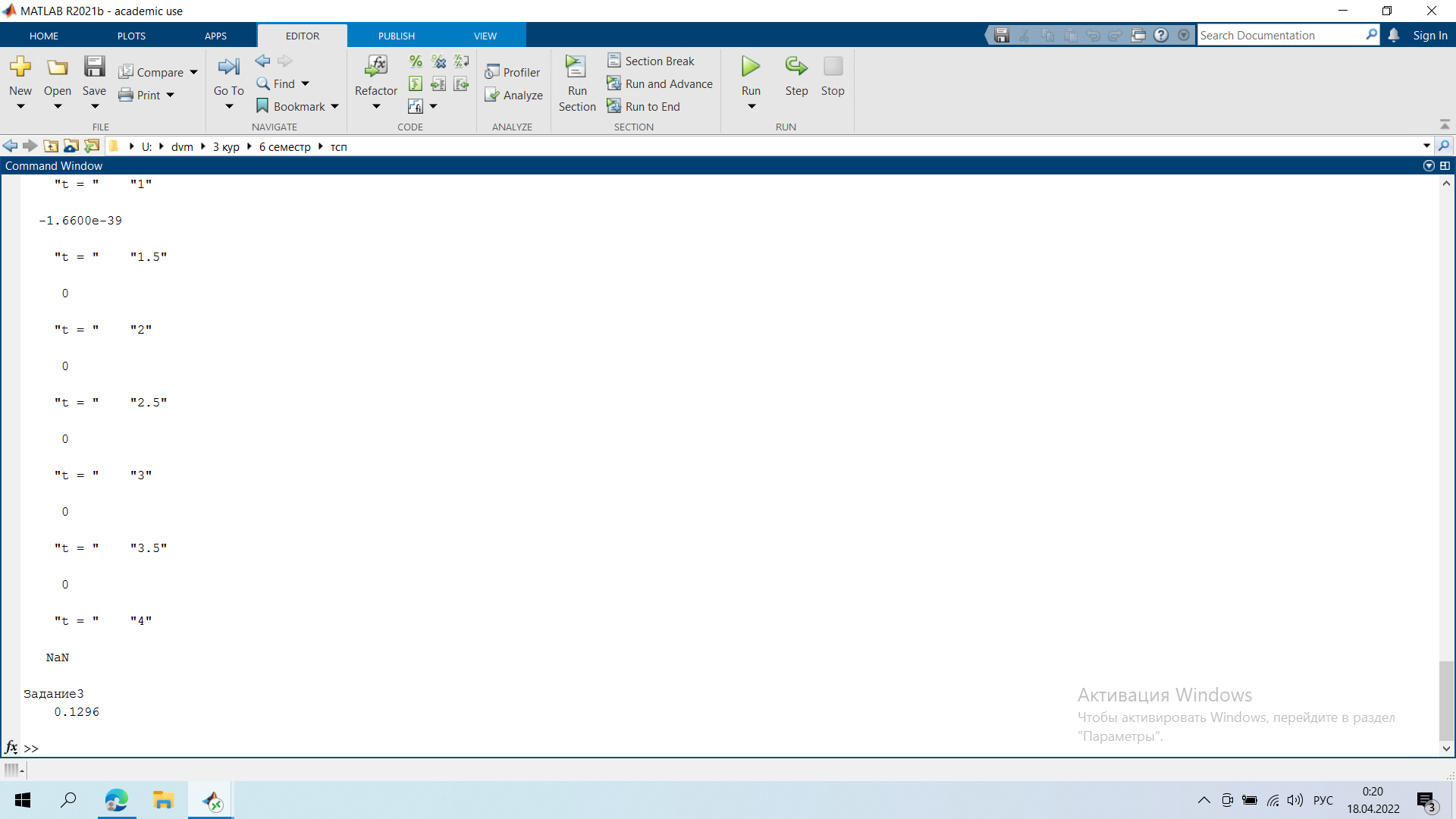 Графики: 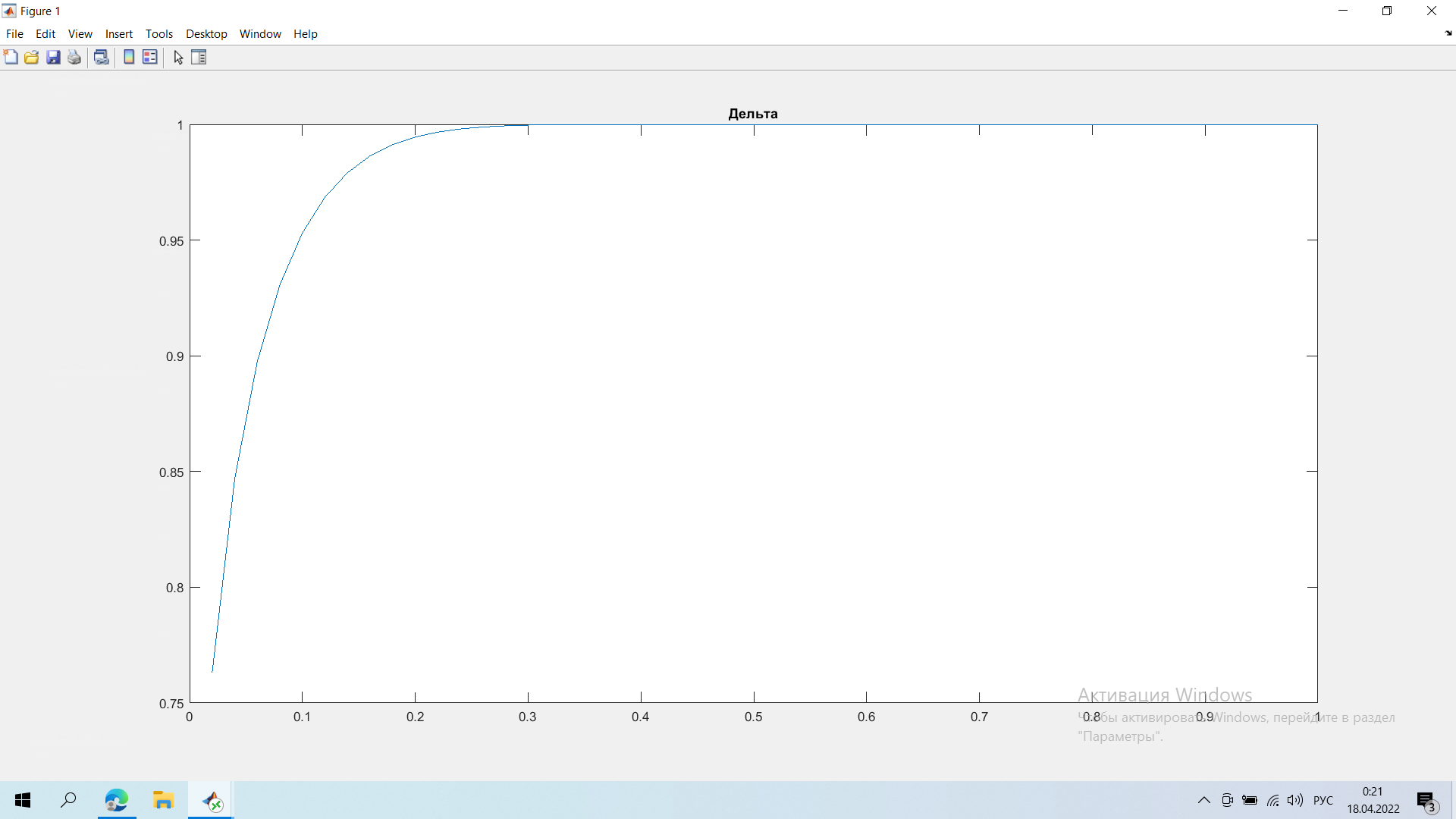 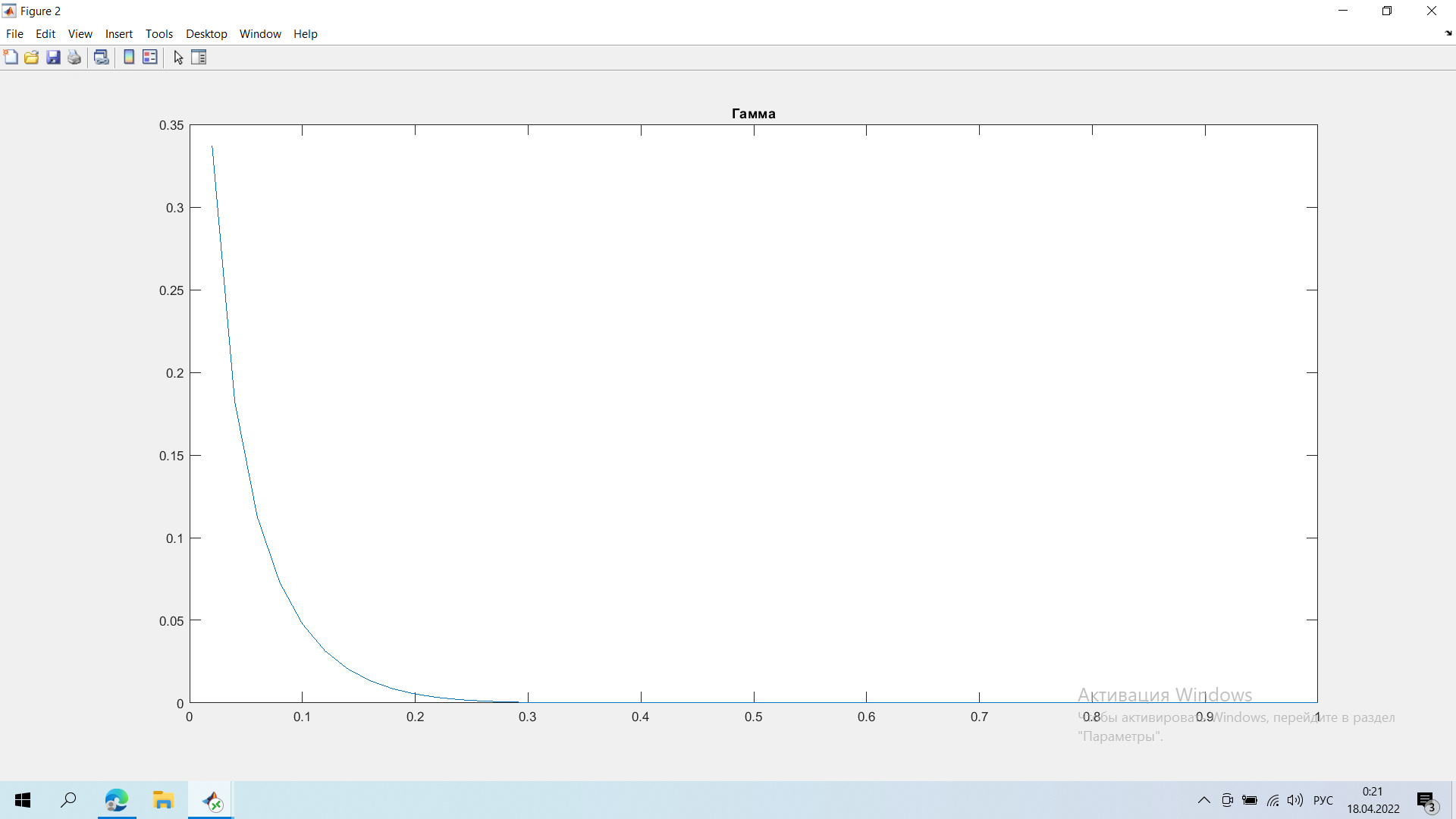 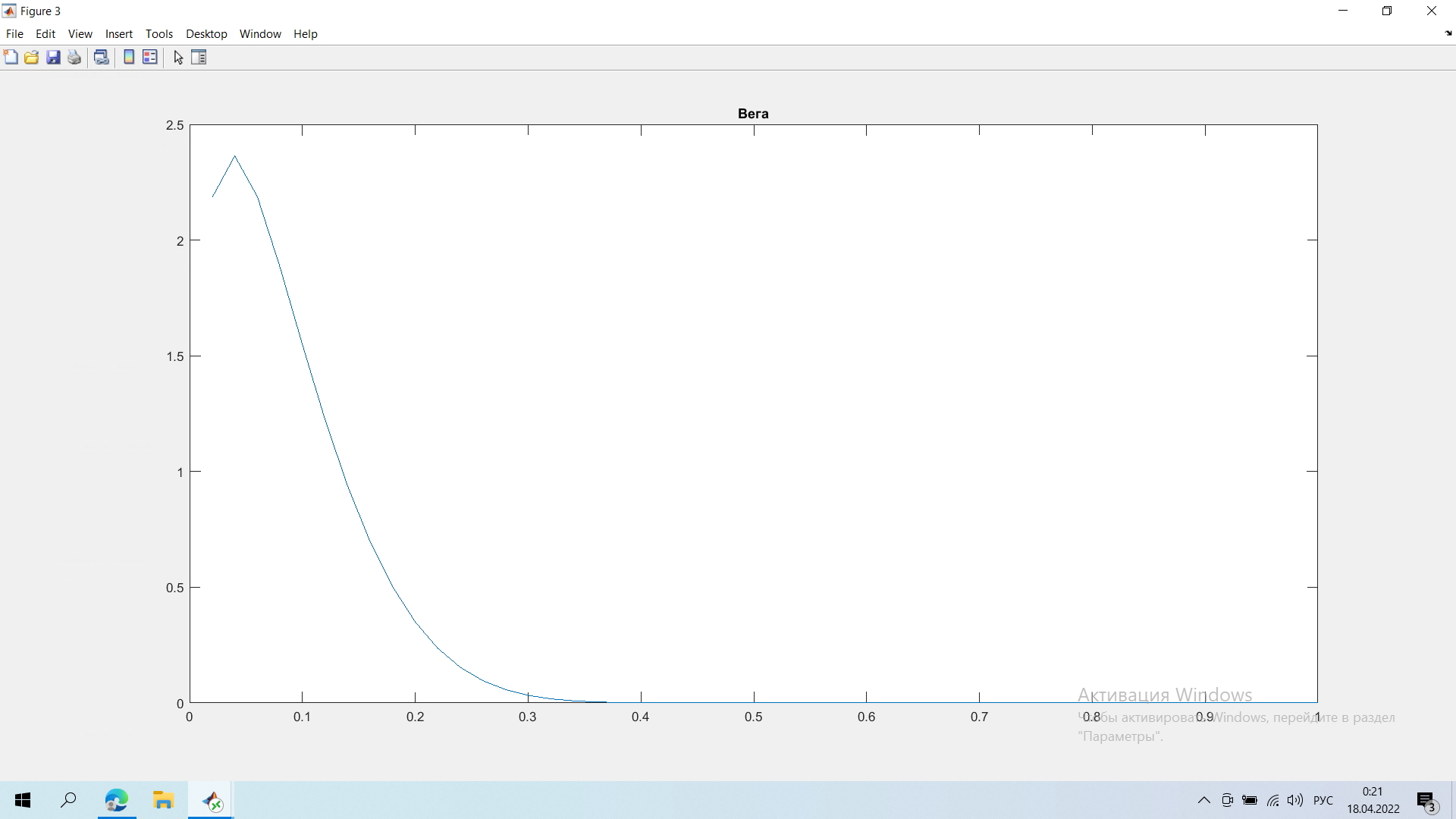 Вывод: в ходе выполнения лабораторной работы можно заметить, что значение последнего графика в момент исполнения t = 0 достигает нуля, были найдены годовая реализованная волатильность σ - приращений, справедливая цена опциона в момент времени t=1 и минимальная доходность портфеля |