Расчёт количества информации и энтропии для дискретных сообщений. ЛР 4. Лабораторная работа 4 по дисциплине Основы теории информации
 Скачать 27.01 Kb. Скачать 27.01 Kb.
|
|
МИНОБРНАУКИ РОССИИ Юго-Западный государственный университет Факультет фундаментальной и прикладной информатики полное наименование факультета Кафедра космического приборостроения и систем связи полное наименование кафедры Направление подготовки (специальность) 11.03.02 Инфокоммуникационные технологии и системы связи шифр и название направления подготовки, специальности Лабораторная работа №4 по дисциплине «Основы теории информации» «Расчёт условной энтропии дискретных сообщений, передаваемых по каналу связи с помехами» Вариант № 5 студента 3 курса группы ИТ-81з курса, группы Белоусова Александра Юрьевича ____________________ фамилия, и. о. подпись, дата Проверил Преподаватель Коптев Дмитрий Сергеевич 2021 г. Цель работы: приобрести умение определять условную энтропию, энтропию объединения и информационные потери для дискретных сообщений, передаваемых по каналу связи, в котором присутствуют помехи. Основные теоретические сведения Понятие условной энтропии в теории информации используется при определении взаимозависимости между символами кодируемого алфавита, для определения потерь при передаче информации по каналам связи, при вычислении энтропии объединения. При нахождении условной энтропии в том или ином виде используются условные вероятности. Если при передаче N сообщений символ а появится М раз, символ b появится L раз, а символ а вместе с символом b – К раз, то вероятности появления символов а и b будут p(a)=M/N и p(b)=L/N; вероятность совместного появления символов а и b p(a,b)=K/N. Отсюда условная вероятность появления символа b относительно символа а и условная вероятность появления символа а относительно символа b будут: p(b a )=p(a,b)/p(d)=(K/N)/(M/N)=K/M; p(a b )=p(a,b)/p(b)=(K/N)l(L/N)=K/L. При известной условной вероятности можно определить вероятности совместного появления символов: p(a,b)=p(a)p(b a )=p(b)p(a b ). Условная энтропия источника сообщений В относительно источника А характеризует степень неопределенности в сообщении из источника В, при известном сообщении из источника A. Условная энтропия источника сообщений В относительно источника А характеризует степень неопределенности в сообщении из источника В, при известном сообщении из источника A. Энтропия объединения Н(А,В) характеризует неопределенность того, что было послано сообщение из источника А, а принято сообщение из источника В. Ход работы: Пусть при передаче сообщений по каналу связи с шумами была получена следующая статистика: символ s1 из 100 раз был принят 99 раз, 1 раза был принят символ s2; при передаче s2 97 раз был принят s2, 1 раза – s1,и 2 раза s3; при передаче s3 99 раз был принят s3, 1 раза – s1; при передаче s4 97 раз был принят s4 и 1 раз – s2 и 2раза-s3 . Вероятности появления этих символов в передаваемых сообщениях соответственно равны: p(s1) = 0,29; p(s2) = 0,16; p(s3) = 0,31; p(s3) = 0,24. Канальная матрица будет иметь следующий вид: P(a/b)= 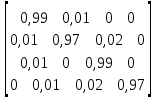 Определим общую условную энтропию сообщений: H(b/a)= - 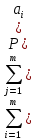 )P( )P(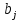 | |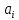 ) ) P( P(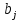 | |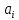 ); );H(b/a)=-[ 0,29*(0,99-  0,99+0,01- 0,99+0,01- 0,01)+0,16*(0,01- 0,01)+0,16*(0,01- 0,01+0,97- 0,01+0,97- 0,97+0,02- 0,97+0,02- 0,02) )+0,31*(0,01- 0,02) )+0,31*(0,01-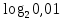 +0,99- +0,99- 0,99)+0,24*(0,01- 0,99)+0,24*(0,01- 0,01+0,02- 0,01+0,02- 0,02+0,97- 0,02+0,97- 0,97)=0,9818бит/символов 0,97)=0,9818бит/символовОпределим энтропию принятых сообщений: H(b/a)=- 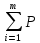 ( (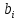 ) ) P(bj); P(bj);P(b1)=0,29*0,99+0,16*0,01=0,2887 P(b2)=0,29*0,01+0,31*0,01+0,16*0,97=0,1612 P(b3)=0,290 ; P(b4)=0,168 H(B)=0,2917  0,2917+0,392 0,2917+0,392 0,392+0,29 0,392+0,29 0,29+0,168 0,29+0,168 0,168=0,489+0,529+0,494+0,432=2,114 бит/символов 0,168=0,489+0,529+0,494+0,432=2,114 бит/символовСоставим матрицу совместных вероятностей, определив для этого все совместные вероятности: ( a 1 b 1 ) = 0,29 0,99 = 0,2871; p(a 2 b3) = 0,29 0 = 0; p(a 2 b1) = 0,16 0,01 = 0,0016; p(a 2 b3) = 0,16 0,02 = 0,0032; p(a 3 b1) = 0,31 0,01 = 0,0031; p(a 3 b3) = 0,31 0 = 0; p(a 4 b1) = 0,24 0,01 = 0,0024; p(a 4 b3) = 0,24 0,97 = 0,2328; p(a 1 b2) = 0,29 0,01 = 0,0029; p(a 1 b4) = 0,29 0 = 0; p(a 2 b2) = 0,16 0,97 = 0,1552; p(a 2 b4) = 0,16 0= 0; p(a 3 b2) = 0,31 0,99 = 0,3069; p(a 3 b4) = 0,31 0 = 0; p(a 4 b2) = 0,24 0,02 = 0,00048; p(a 4 b4) = 0,24 0 = 0; P(a/b)= 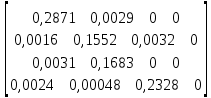 Определим энтропию объединения: H(a,b)=- 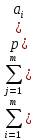 , ,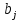 ) ) p( p(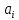 , ,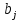 ) )H(a,b)=(0,2871*  0,2871+0,0029 0,2871+0,0029 0,0029+0,0016 0,0029+0,0016 0,0016+0,1552 0,0016+0,1552 0,1552+0,0032 0,1552+0,0032 0,0032+0,0031 0,0032+0,0031 0,0031+0,3069 0,0031+0,3069 0,3069+0,0024 0,3069+0,0024 0,0024+0,00048 0,0024+0,00048 0,00048+0,2328 0,00048+0,2328 0,2328=2,284 бит/символов 0,2328=2,284 бит/символовНайдем информационные потери при передаче 500 символов: 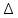 I=n*H(A|B); I=n*H(A|B);H(A|B)=H(A,B)-H(B). H(A|B)=2,284-2,144=0,14 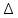 I=500*0,14=70 бит I=500*0,14=70 битОтсюда количество принятой информации будет: 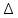 I=I*H(B)- I=I*H(B)-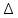 I; I;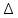 I=500*2,144-70=1072 бит I=500*2,144-70=1072 битВывод: В ходе выполнения работы приобрели умение определять условную энтропию, энтропию объединения и информационные потери для дискретных сообщений, передаваемых по каналу связи, в котором присутствуют помехи. Контрольные вопросы 1. Что характеризует и как определяется условная энтропия одного дискретного источника сообщений относительно другого? Общая условная энтропия системы - относительно системы А характеризует количество информации, содержащейся в любом символе источника сообщений, через который мы представляем состояния элементов исследуемых систем. Общую условную энтропию определяют путем усреднения по всем символам, т. е. по всем состояниям аi с учетом вероятности появления каждого из них. 2.В каком случае условная энтропия равна нулю? H(Y|X)=0тогда и только тогда, когда значение полностью определяется значением YX. 3. Как строится и что характеризует канальная матрица? Канальная матрица (КМ) – квадратная матрица размером 4. Чему равна энтропия объединения источников сообщений при их полной статистической зависимости? Энтропия равна нулю в том крайнем случае, когда одно событие равно единице, а все остальные – нулю. Это положение соответствует случаю, когда состояние источника полностью определено. 5. Как связана энтропия объединения и условная энтропия двух статистически зависимых источников сообщений? Условная энтропия статистически зависимых источников сообщений. Независимые источники: если 2 независимых источника с объемами алфавитов М и К рассматривать как 1 источник, кот. одновременно реализует пары состояний мi и кi, то полагают что энтропия объединения равна сумме энтропий отдельных источников. 6. Как определяются информационные потери при передаче сообщений по каналу связи с помехами? Определение информационных потерь в каналах связи. Производится с помощью вычисления условной энтропии. Составляется канальная матрица. Пусть по каналу связи источником информации передаются сигналы x1, x2, …, xm . На другом конце канальной связи существует приёмник, который принимает сигнал y1, y2, …, ym . |
