Комьютерые сети. Лабораторная работа 4-2020. Лабораторная работа 4 по курсу "Методы и средства защиты информации" Модулярная арифметика
 Скачать 23.4 Kb. Скачать 23.4 Kb.
|
Лабораторная работа №4по курсу "Методы и средства защиты информации" Модулярная арифметика. Определение обратного элемента в конечном поле. Рабочее задание. 1. Последовательно определить значения вычетов по модулю 5 (Mod[***,5]) для чисел: 0,1,2,3,4,5,6,7,8,9,10. 2. Провести операцию вычисления вычета по модулю 5 для списка list0 = Range[0,10]. 3. На множестве целых чисел создать четыре класса эквивалентности (списка) для операции Mod[***, pN], где pN – простое число с номером Nсгр + 10, а Nсгр – номер по списку в группе: list1 = {-2pN+1,....,- pN }; list2 = {-pN+1,...., 0 }; list3 = {0,...., pN-1 }; list4 = {pN,....,2pN-1 }. 4. Привести по модулю pN элементы каждого из четырех списков, а затем отсортировать результаты (res1,res2,res3,res4) в порядке возрастания – Sort[***,Less]. 5. Провести проверку эквивалентности списков res1,res2,res3,res4 двумя способами: а) при помощи оператора If[], логических функций сравнения == (Equal) и логического "и" && (And); Результат проверки вывести с помощью опертора Print[] в виде: "Списки совпадают" или "!!!Списки не совпадают"; б) провести проверку с помощью функции Equivalent[]. 6. Для чисел a = 5+Nсгр , b=10+Nсгр , c=15+Nсгр и модуля pm= NextPrime[6+Nсгр] провести проверку эквивалентности следующих операций модулярной арифметики: 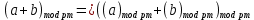 ; ;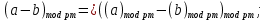 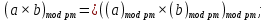 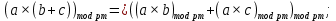 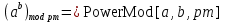 7. В конечном поле GF[pN] для числа s = Floor[pN /2] найти обратный элемент по сложению s', такой, что 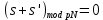 . .В конечном поле GF[pN] для числа 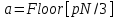 , найти число , найти число 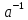 , обратное числу а по умножению, поочередно проверяя значения 1, 2, … , обратное числу а по умножению, поочередно проверяя значения 1, 2, … 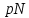 -1, пока не будет найдено -1, пока не будет найдено 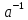 , такое что , такое что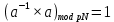 . Поиск выполнить используя операторы пакета «Математика» - Do, While, For. Вариант реализации определяется из следующего соотношения nv = Nсгр (mod3)+1 и таблицы: . Поиск выполнить используя операторы пакета «Математика» - Do, While, For. Вариант реализации определяется из следующего соотношения nv = Nсгр (mod3)+1 и таблицы:
Программная реализация алгоритма должна быть выполнена в виде функции пользователя на основе оператора Module[] с двумя входными параметрами: a и p, а также с тремя выходными: a, a-1, p. Реализовать расширенный алгоритм Евклида, найти вектор “u” и число а-1, обратное по умножению к числу а по модулю pN. Для верификации алгоритма применить a = 5 и модуль p = 23. Программная реализация алгоритма должна быть выполнена в виде функции пользователя на основе оператора Module[] с двумя входными параметрами: a и p, и двумя выходными: а-1 и {u1,u2,u3}. Сравнить полученные результаты с результатом выполнения встроенной функции ExtendedGCD[pN,a]. Определить значение функции Эйлера для модуля pN : 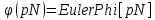 . .Найти число 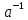 , обратное числу а по модулю pN, путем прямого вычисления , обратное числу а по модулю pN, путем прямого вычисления 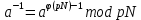 . .Построить полную и приведенную систему вычетов по модулю 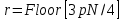 , с использованием функции GCD[]. Определить число элементов полной и приведенной системы. Программная реализация алгоритма должна быть выполнена в виде функции пользователя на основе оператора Module[], входной параметр: r ,выходные параметры: список элементов полной системы, его длина, список приведенной системы вычетов, его длина. Сравнить полученные результаты с результатом вычисления функции EulerPhi[]. , с использованием функции GCD[]. Определить число элементов полной и приведенной системы. Программная реализация алгоритма должна быть выполнена в виде функции пользователя на основе оператора Module[], входной параметр: r ,выходные параметры: список элементов полной системы, его длина, список приведенной системы вычетов, его длина. Сравнить полученные результаты с результатом вычисления функции EulerPhi[].Определить число 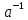 , обратное числу а по модулю pN, используя функцию PowerMod [ , , ]. , обратное числу а по модулю pN, используя функцию PowerMod [ , , ].Используя встроенную функцию Timing[], определить время поиска обратного элемента в п.8 для следующих значений модуля : 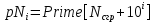 , где i , где i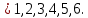 Перед каждым измерением времени необходимо очистить системный кэш - ClearSystemCache[]. Сравнить время выполнения операции, выполненой по алгоритму п.8 со временем выполнения операции PowerMod[] для i=6. |
