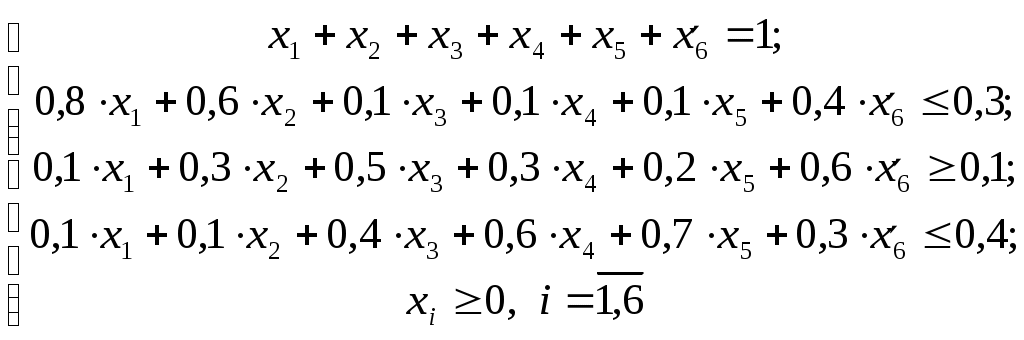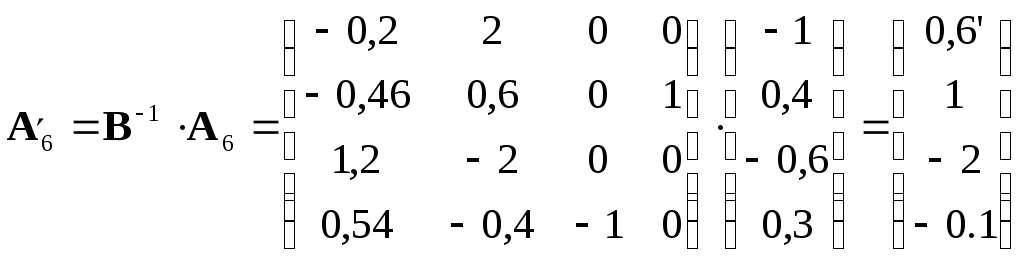3. Анализ чувствительности оптимального решения задачи к изменению технологических коэффициентов.
В этом пункте, как и в предыдущем, можно рассматривать два случая: изменение значений коэффициентов, соответствующих базисным переменным и свободным переменным. Изменение значений коэффициентов при базисных переменных приводит к изменению базисной матрицы, поэтому проанализировать это довольно сложно, ленче решить задачу заново. Следовательно. Рассмотрим случай с изменением коэффициента при свободной переменной.
Возьмем, например, как изменяющийся коэффициент 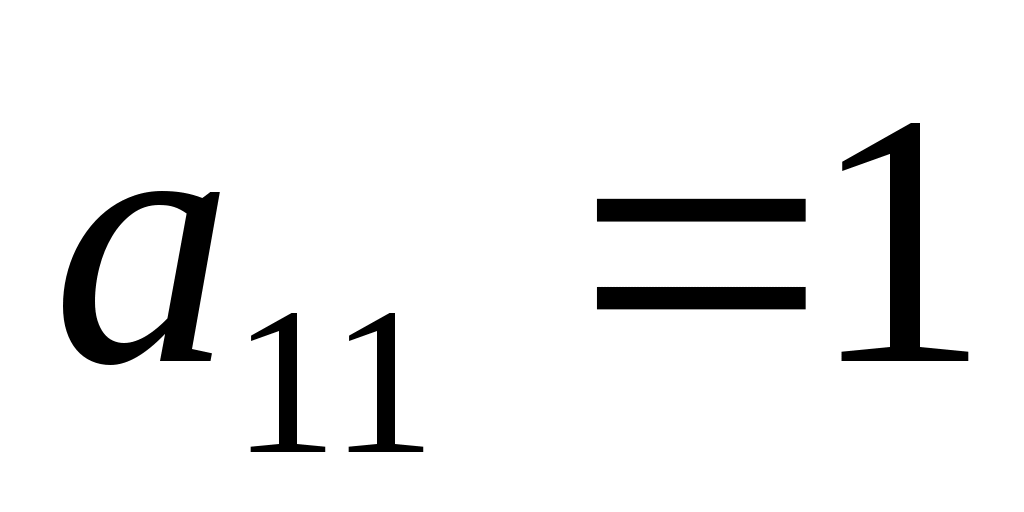 . Его изменение влечёт за собой изменение оценки только свободной переменной . Его изменение влечёт за собой изменение оценки только свободной переменной 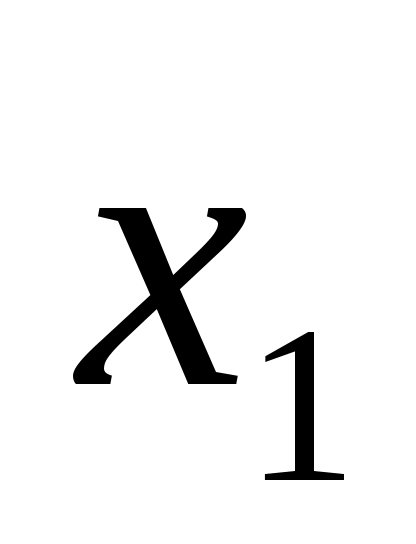 : :
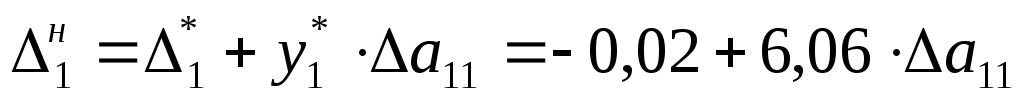 . Для того, чтобы решение оставалось оптимальным, необходима неположительность оценки: . Для того, чтобы решение оставалось оптимальным, необходима неположительность оценки: 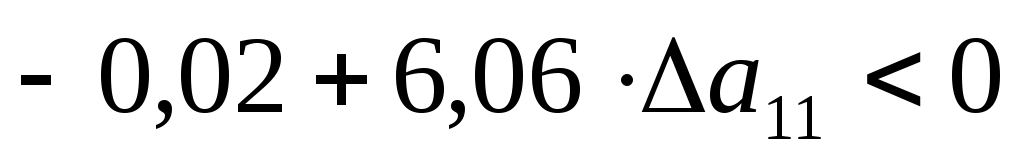 т.е. т.е. 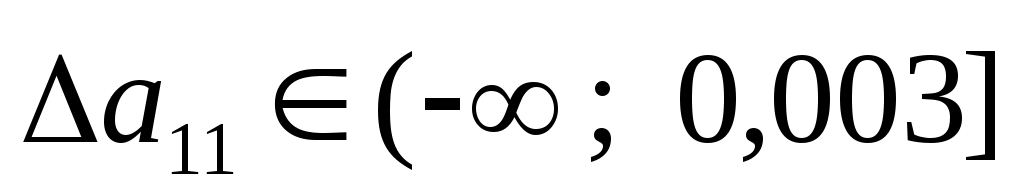 . Интервал устойчивости коэффициента . Интервал устойчивости коэффициента 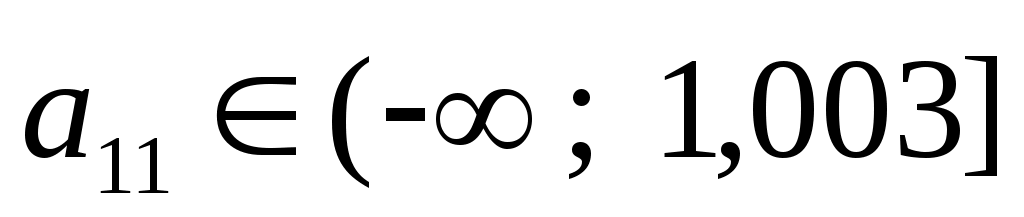 . .
Возьмём также для наглядности изменение ещё одного коэффициента, т.к. полученный выше результат означает, что содержание сплава (т.е всех компонентов) в первом сырье может меняться от 0% до 100% (формально от 0% до 100,3%).
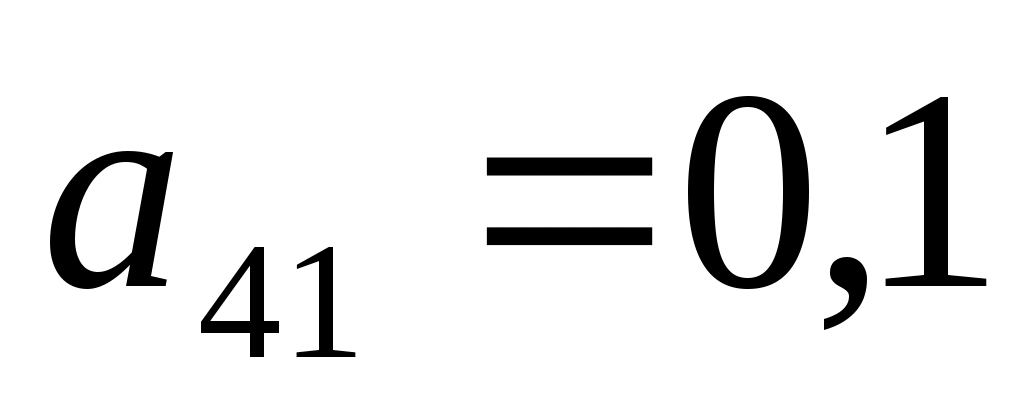 , , 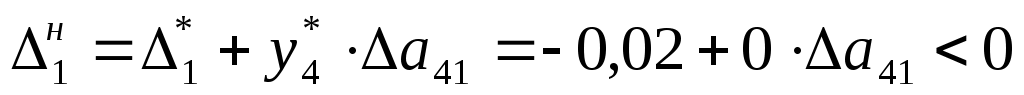 , , 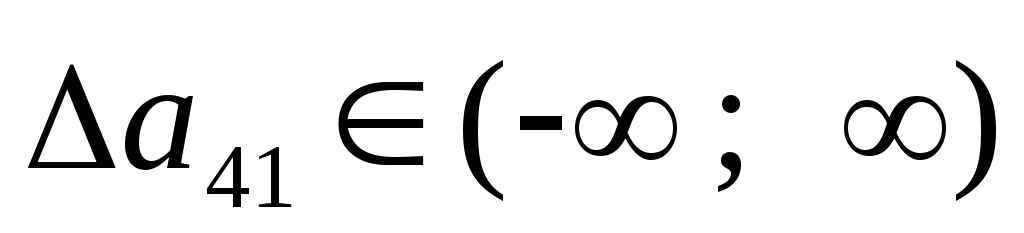 , , 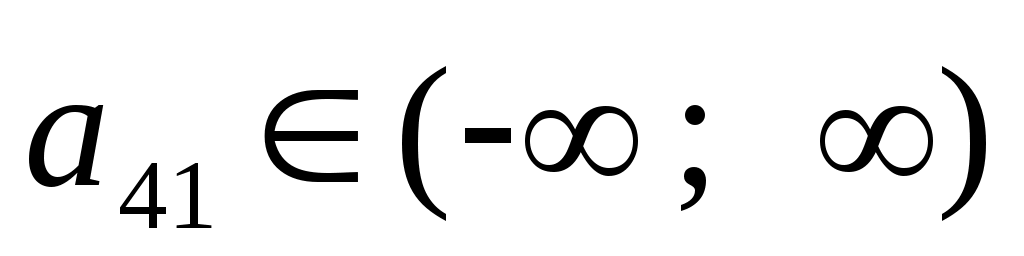 , т.е. содержание свинца в первом сырье варьируется в пределах от 0% до 100% ( , т.е. содержание свинца в первом сырье варьируется в пределах от 0% до 100% ( и и  экономического смысла не имеют). экономического смысла не имеют).
В качестве примера только из чистого математического любопытства приведем такую фантастическую ситуацию: содержание сплава в первом сырье возросло до:
а) 100,2%
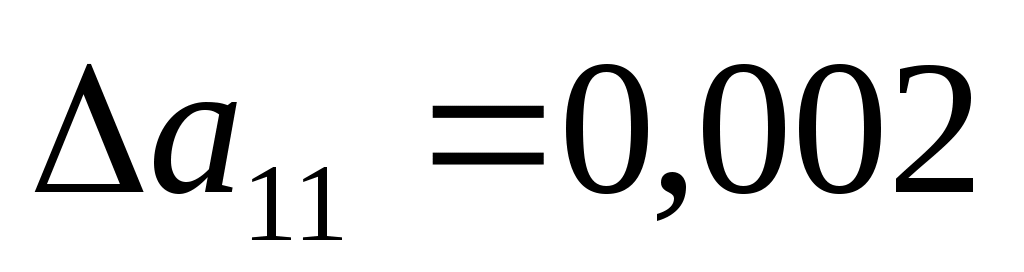 , ,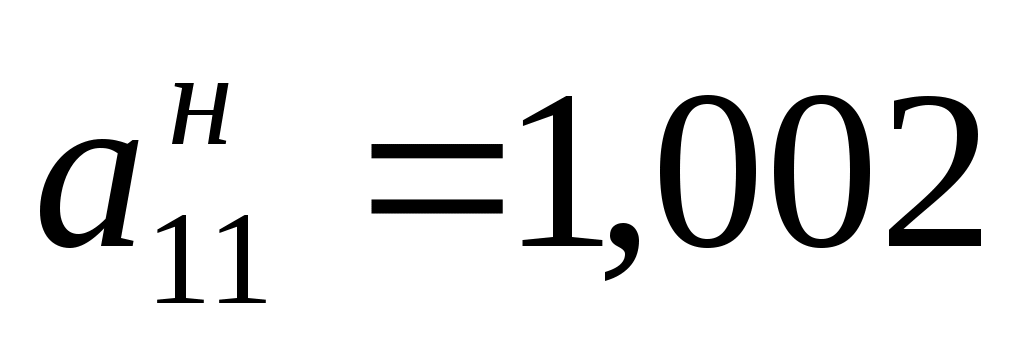 (входит в интервал устойчивости). Оптимальный план выпуска не изменится (входит в интервал устойчивости). Оптимальный план выпуска не изменится 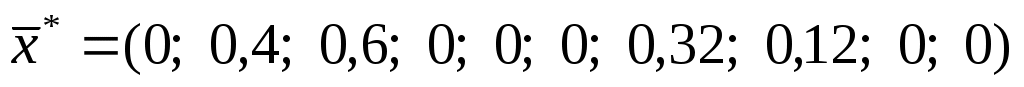 и оптимальное значение целевой функции останется и оптимальное значение целевой функции останется  . .
б) 110%
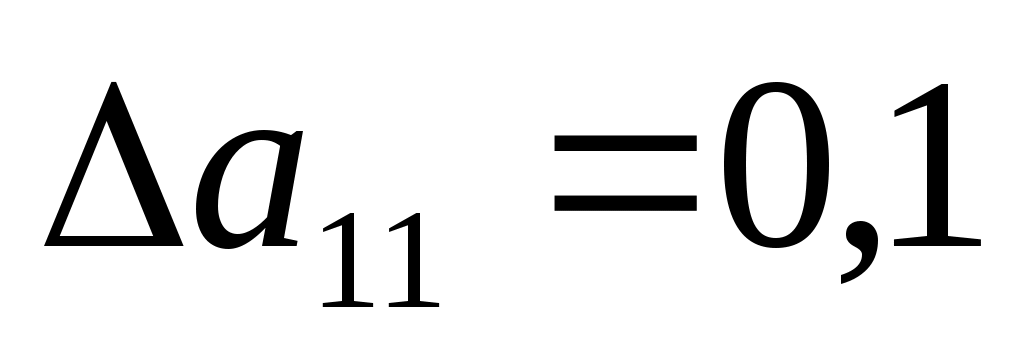 , , 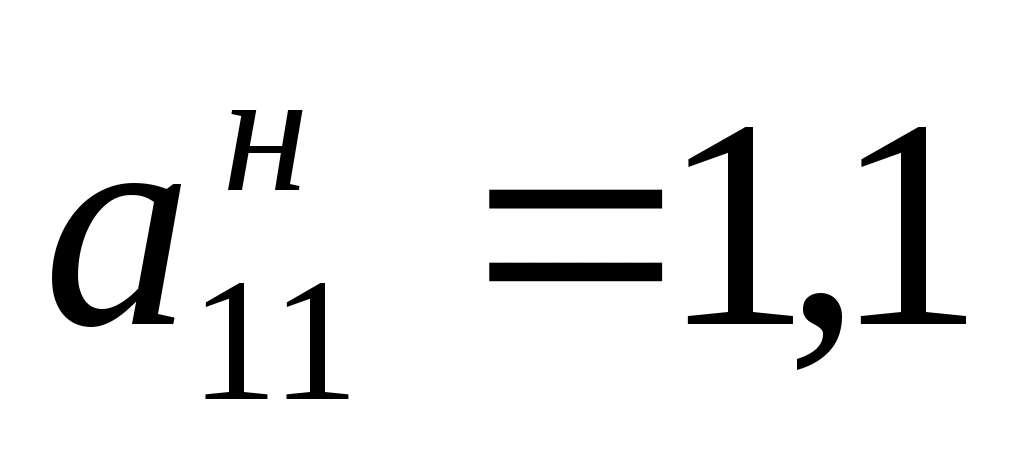 (не входит в интервал устойчивости). (не входит в интервал устойчивости).
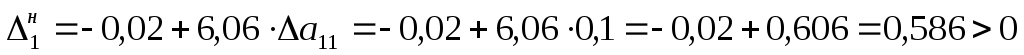 – оценка не оптимальная. – оценка не оптимальная.
Симплекс-методом получим оптимальное решение:
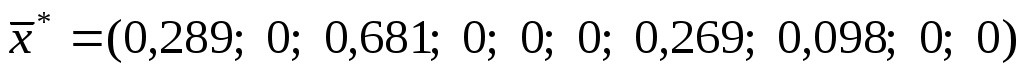 , , 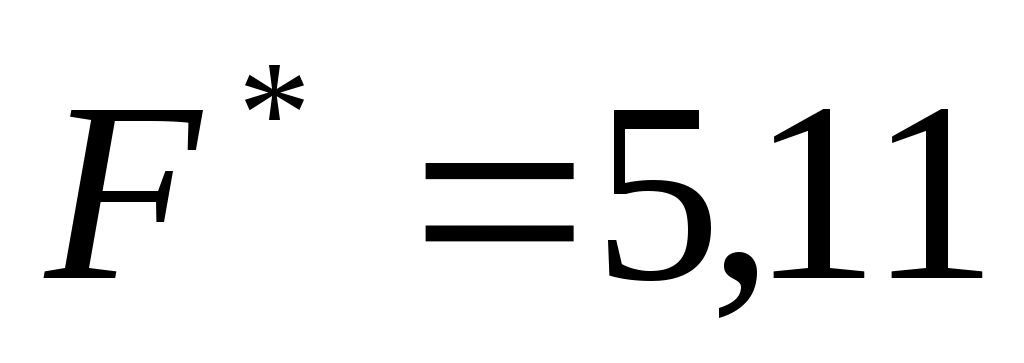 . .
4. Введение новой переменной.
Предположим, что появилась возможность использовать новый вид сырья, в котором содержится 40% олова, 60% цинка и 30% свинца, и который обладает стоимостью 3,5 у.е. за единицу. Определим новый план производства.
Пусть 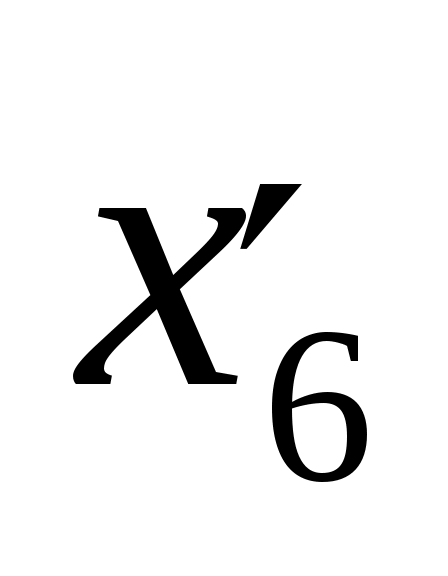 – доля шестого (нового) сырья в сплаве. Тогда: – доля шестого (нового) сырья в сплаве. Тогда:
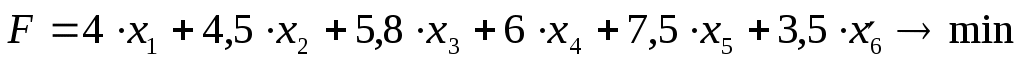
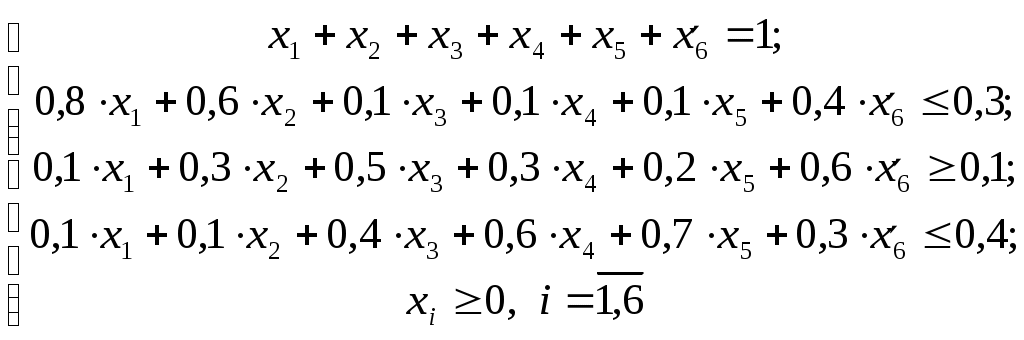
Решим, выгодно ли использовать новое сырьё. Для этого воспользуемся двойственными оценками  . .
Доход на тонну нового сырья будет равен 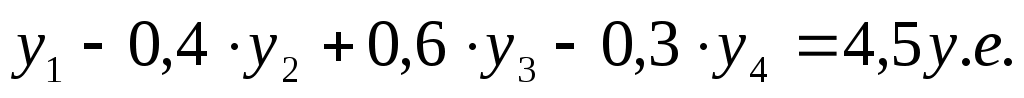 , а затраты – 3,5 у.е. (Новое ограничение в двойственной задаче , а затраты – 3,5 у.е. (Новое ограничение в двойственной задаче 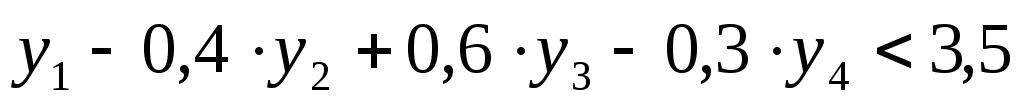 ) Тонна сырья приносит больше дохода, чем издержек на 1 у.е., поэтому будем увеличивать использование этого сырья. ) Тонна сырья приносит больше дохода, чем издержек на 1 у.е., поэтому будем увеличивать использование этого сырья.
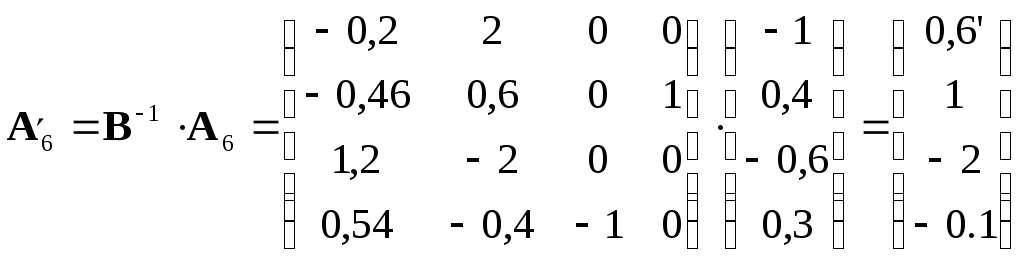
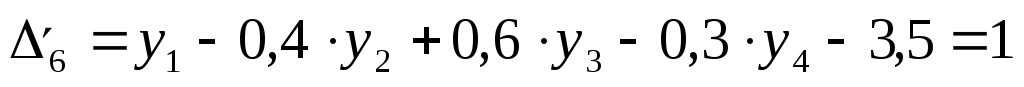
Запишем новую симплекс-таблицу с учётом новой переменной:
|
4
|
4,5
|
5,8
|
6
|
7,5
|
3,5
|
0
|
0
|
0
|
0
|
0
|
|
Св
|
Б.П.
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6’
|
X6
|
X7
|
X8
|
X9
|
X10
| В |
4,5
|
X2
|
1,4
|
1
|
0
|
0
|
0
|
0,6’
|
2
|
0
|
0
|
-0,2
|
0
|
0,4
|
0
|
X8
|
0,12
|
0
|
0
|
0,2
|
0,3
|
1
|
0,6
|
0
|
1
|
-0,46
|
0
|
0,12
|
5,8
|
X3
|
-0,4
|
0
|
1
|
1
|
1
|
-2
|
-2
|
0
|
0
|
1,2
|
0
|
0,6
|
0
|
X7
|
0,12
|
0
|
0
|
0,2
|
0,3
|
-0,1
|
-0,4
|
1
|
0
|
0,54
|
-1
|
0,32
|
|
F
|
-0,02
|
0
|
0
|
-0,2
|
-1,7
|
1
|
-2,6
|
0
|
0
|
-6,06
|
0
|
5,28
|
Оптимальная симплекс-таблица:
|
4
|
4,5
|
5,8
|
6
|
7,5
|
3,5
|
0
|
0
|
0
|
0
|
0
|
|
Св
|
Б.П.
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6’
|
X6
|
X7
|
X8
|
X9
|
X10
| В |
3,5
|
X6’
|
2,333
|
1,666
|
0
|
0
|
0
|
1
|
3,333
|
0
|
0
|
-0,333
|
0
|
0,666
|
0
|
X8
|
-0,066
|
-0,133
|
0
|
0,2
|
0,3
|
0
|
0,333
|
0
|
1
|
-0,433
|
0
|
0,066
|
5,8
|
X3
|
-1,33
|
-0,666
|
1
|
1
|
1
|
0
|
-3,33
|
0
|
0
|
1,333
|
0
|
0,333
|
0
|
X7
|
0,633
|
0,366
|
0
|
0,2
|
0,3
|
0
|
0,333
|
1
|
0
|
0,466
|
-1
|
0,466
|
|
F
|
-3,56
|
-2,53
|
0
|
-0,2
|
-1,7
|
0
|
-7,66
|
0
|
0
|
-6,566
|
0
|
4,266
|
Оптимальное решение будет 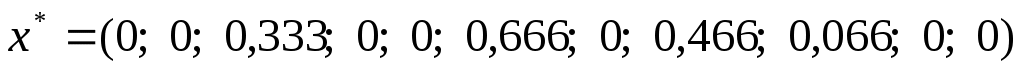 , , 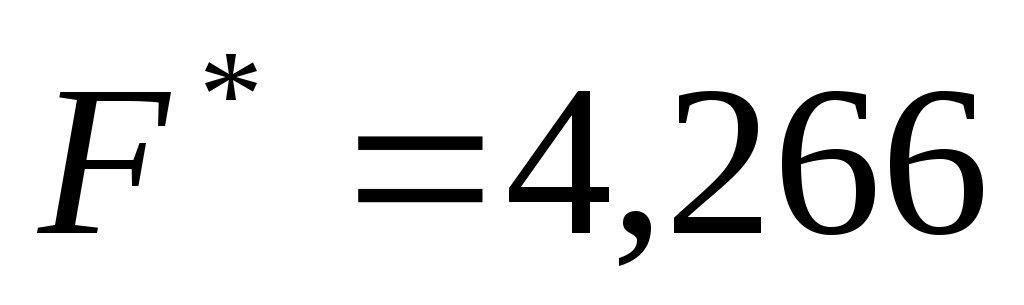 . Это означает, что для производства нового сплава будет использоваться 33,3% третьего сырья и 66,6% нового шестого сырья. Минимальная стоимость сплава будет 4,266 у.е. Видим, что использование нового вида сырья действительно выгодно, т.к. издержки на производство сплава снизились с 5,28 у.е. за единицу до 4,266 у.е. . Это означает, что для производства нового сплава будет использоваться 33,3% третьего сырья и 66,6% нового шестого сырья. Минимальная стоимость сплава будет 4,266 у.е. Видим, что использование нового вида сырья действительно выгодно, т.к. издержки на производство сплава снизились с 5,28 у.е. за единицу до 4,266 у.е.
|
 Скачать 0.52 Mb.
Скачать 0.52 Mb.