лаба 4. Лабораторная работа 4 Телешовой Елизаветы, гр. 726
 Скачать 0.52 Mb.
|
2.Анализ чувствительности оптимального решения задачи к изменению коэффициентов целевой функции.Определим интервал устойчивости решения к изменению стоимости сырья, то есть, в каких пределах могут меняться цены на сырьё, чтобы план выпуска сплава не изменился. Для этого рассмотрим два случая: изменение цен (коэффициентов целевой функции) происходит на сырьё, использующееся при производстве сплава (базисные переменные) и не использующееся (свободные переменные). 1. Пусть, сначала, меняется цена второго и третьего ресурсов (базисные переменные). а)  .Тогда оптимальная симплекс-таблица будет иметь вид:
Для того, чтобы решение оставалось оптимальным, необходимо, чтобы все оценки были неположительными (для задачи на минимум): 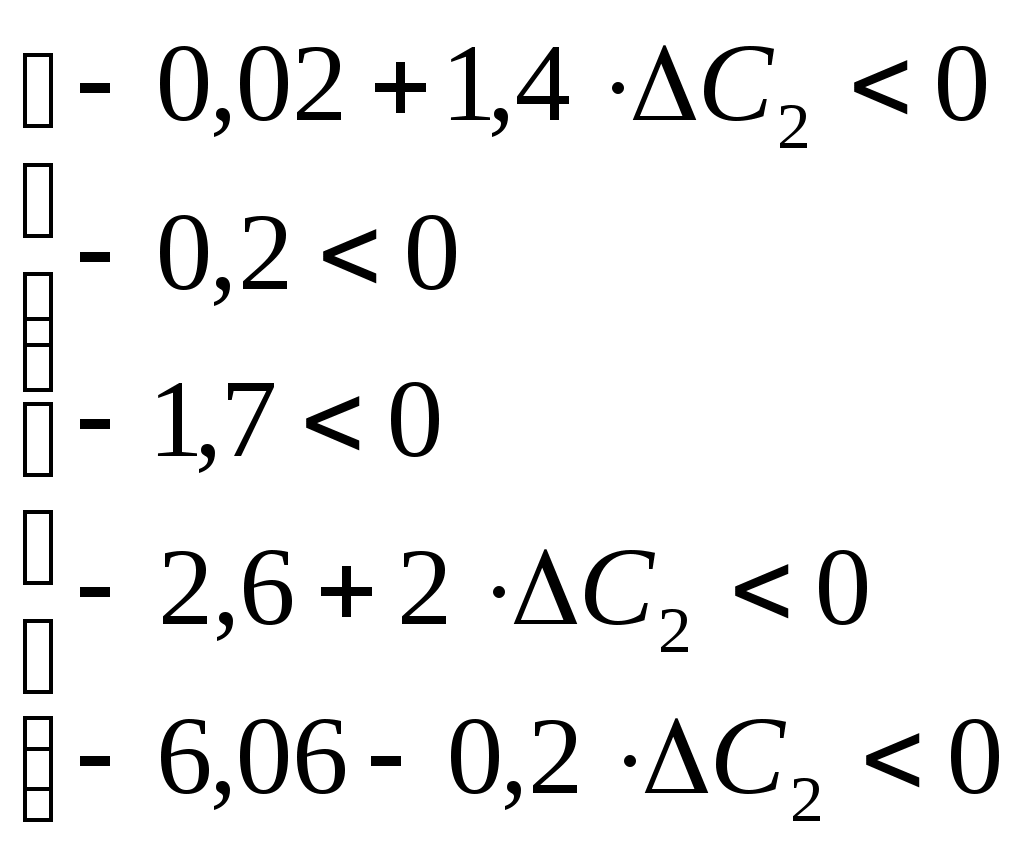 =>  ,  Это значит, что цена первого ресурса может меняться от нуля (бесплатный, недефицитный ресурс) до 4,514 у.е. (отрицательный коэффициент в целевой функции в данном случае не имеет экономического смысла, т.к. свидетельствует о получении ресурса с доплатой. В этом случае ресурс выступает в роли антиблага). Критерий изменится на  .б) 
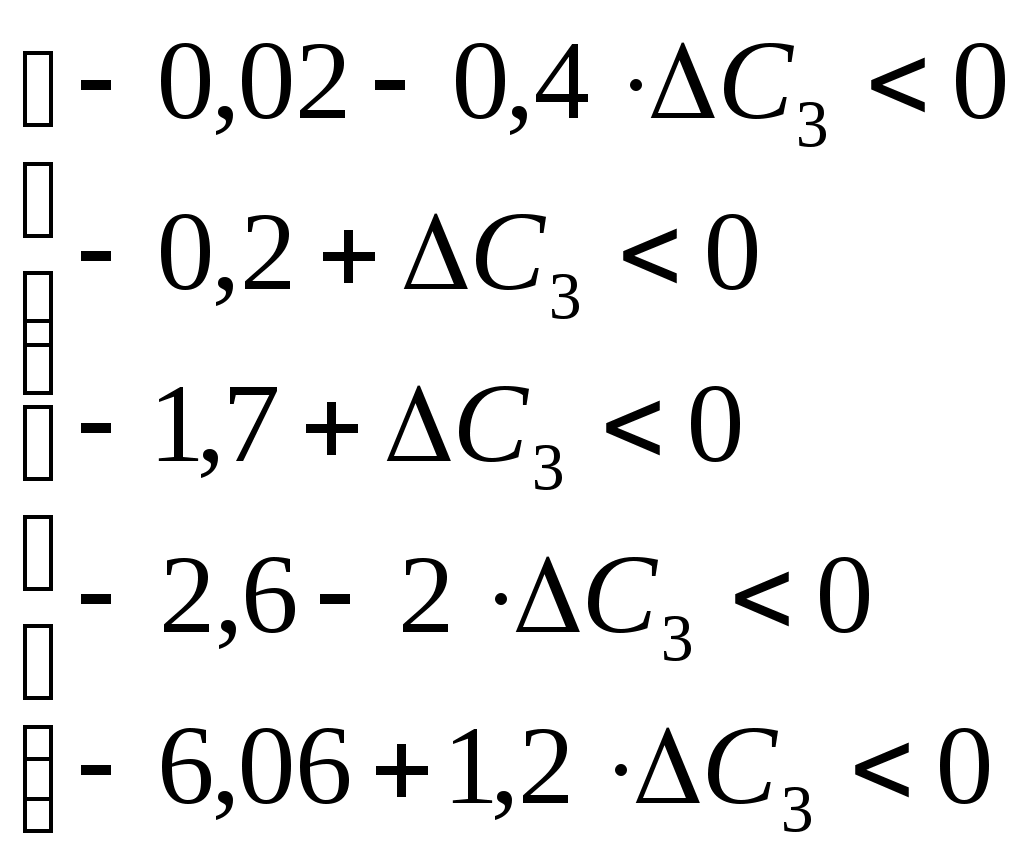 =>  ,  Коэффициент критерия может меняться от 5,75 у.е. за одну тонну третьего сырья до 6 у.е. При этом решение будет оставаться оптимальным, а сам критерий изменится на  .2. Рассмотрим случай со свободной переменной. а)  , тогда  Условие оптимальности оценки:  =>  =>  .В данном случае  ,  .Таким образом, решение будет оставаться оптимальным, при уменьшении коэффициента при  до 3,98 у.е. за единицу и неограниченном увеличении. Значение целевой функции при этом не изменится.б) Будем руководствоваться аналогичными рассуждениями при вычислении интервалов устойчивости для четвёртого и пятого ресурсов.  ,  или  , . ,  или  , Оптимальные решения при конкретных изменениях коэффициентов. а)стоимость второго сырья увеличилась до 4,5 у.е Интервал устойчивости коэффициента целевой функции . Цена 4,5 у.е. входит в этот интервал, значит оптимальное решение не изменится, а критерий станет  у.е.б) стоимость третьего сырья уменьшилась до 3 у.е Интервал устойчивости для . 3 у.е. ( ) не принадлежит интервалу, значит какие-то оценки будут не оптимальными: – при  :  ;– при  :  ;– при  :  ;– при  :  ;– при  :  ; .Скорректируем симплекс-таблицу:
Через две итерации получаем оптимальную симплекс-таблицу:
Получим оптимальное решение  . Стоимость сплава понизилась до 3 у.е. за единицу.в) издержки на первое сырьё возросли до 6 у.е Стоимость первого сырья может изменяться в пределах  . 6 у.е. входят в интервал, значит оптимальное решение не изменится, а также останется прежнем критерий ( , ).г) издержки на четвёртый ресурс упали до 4 у.е. При падении издержек до 4 у.е. за тонну оптимальное решение должно измениться, т.к. нижняя граница интервала устойчивости – 5,8 у.е. Оценка  .
Оптимальная симплекс-таблица:
С помощью симплекс-метода получаем оптимальное решение  и оптимальное значение критерия  у.е. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
