Лабораторная работа №4 Трехфазные электрические цепи при соединении потребителей электроэнергии звездой и треугольником. Отчет_Звезда. Лабораторная работа 4 Трехфазные электрические цепи при соединении потребителей электроэнергии звездой и треугольником
 Скачать 342.24 Kb. Скачать 342.24 Kb.
|
|
МИНИСТЕРСТВО ВЫСШЕГО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ РОССИЙСКИЙ ХИМИКО-ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Д.И. МЕНДЕЛЕЕВА Кафедра процессов и аппаратов химической технологии Дисциплина: Электротехника и промышленная электроника Лабораторная работа №4 Трехфазные электрические цепи при соединении потребителей электроэнергии звездой и треугольником Вариант № …. Выполнили: Дмитриева С.А. СЕ Селиванова О.А. Группа О-34 Проверил: Логинов Владимир Яковлевич Москва 2021 ЧАСТЬ 1. Трехфазные цепи при соединении потребителей звездой Цель работы: Исследование трехфазных электрических цепей синусоидального тока при соединении потребителей звездой двумя методами: Экспериментальный – имитационное моделирование в среде MultiSim. Расчетный – математическое моделирование в любой среде, например: приложения MathCad, Excel и другие, включая расчет на калькуляторе. Исследование соединения трехфазного потребителя звездой Вариант №1. RA = RB = RC = 21 Ом, LA = LB = LC = 82 мГн, CA = CB = CC = 92 мкФ.
В MultiSim собрана схема трехфазной электрической цепи при соединении генератора и потребителей «звездой». Установлены значения параметров цепи и положения ключей в соответствии с заданным вариантом. 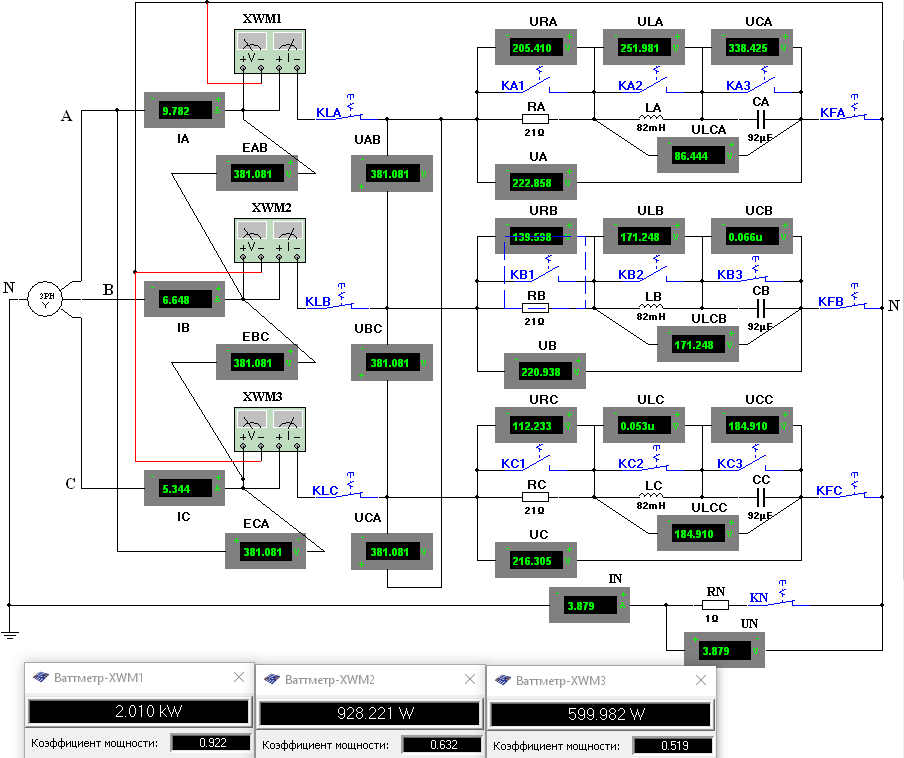 Выполнено исследование трехфазной электрической цепи «звезда – звезда» при изменении положения ключей, согласно заданному варианту, заполнены табл. 4.1 и 4.2. Измерения проводились в MultiSim, расчёты - в MathCad. Таблица 4.1  Таблица 4.2  Различия в значениях Multisim и MathCad для всех нагрузок (кроме короткого замыкания) не составляют и 1%, что свидетельствует о правильно поставленном опыте. Большие отклонения в значениях в режиме КЗ, по всей видимости, связаны с неправильными расчетами в MathCad (хотя при этом значения взяты из пунктов с «уточнением» для КЗ). Расчетные формулы: Z = |R + j(XL - XC)|, XL = ωL, XC = 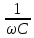 Uf = |E - UN|; UL1 = |Uf1 - Uf2|; UL2 = |Uf2 - Uf3|; UL3 = |Uf3 - Uf1| If = IL = |Uf/Z|; IN = |ƩIf| Si = |Uf· 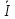 i|, где Uf - напряжение на i-ой фазе (i - A, B, C), i|, где Uf - напряжение на i-ой фазе (i - A, B, C), 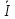 i - сопряженный ток на i-ой фазе i - сопряженный ток на i-ой фазеS = ƩSi φ = arg(Z) Qi = Im(Si), Q = ƩQi Pi = Re(Si), P = ƩPi Средства защиты трехфазных ЭЦ в критических состояниях (обрыв и короткое замыкание): Установка нейтрального провода для предотвращения резких изменений фазных напряжений при обрыве и КЗ. Во избежание ситуаций обрыва нейтрального провода следует его заземлять. В случаях КЗ нейтральный провод может навредить работе приемника, поэтому следует ставить на него (нейтральный провод) предохранитель. Векторные диаграммы фазных напряжений и токов для всех вариантов нагрузки: 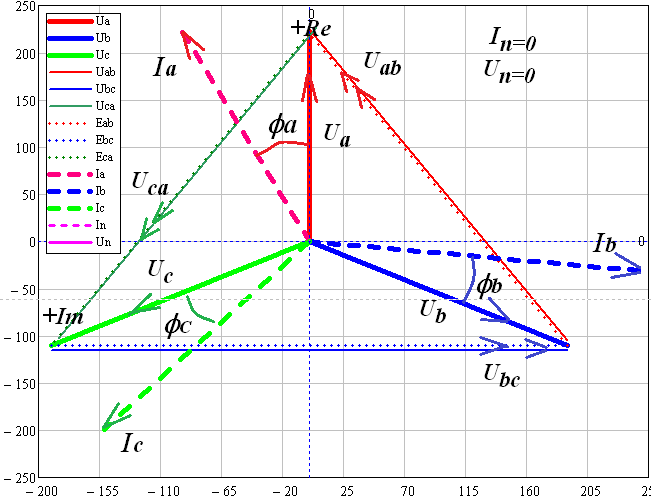 Симметричная нагрузка (KN = 1) Симметричная нагрузка (KN = 1)I опережают U на всех фазах на одинаковые углы, следовательно, нагрузка на них активно-ёмкостная; фазные U одинаковы; линейные U одинаковы.  Симметричная нагрузка (KN = 0) Симметричная нагрузка (KN = 0)Без нейтрального провода ситуация такая же, как и с нейтральным проводом. Значит нужды в нем нет. Диаграммы KN = 0 и KN = 1 идентичны. Несимметричная нагрузка (KN = 1) 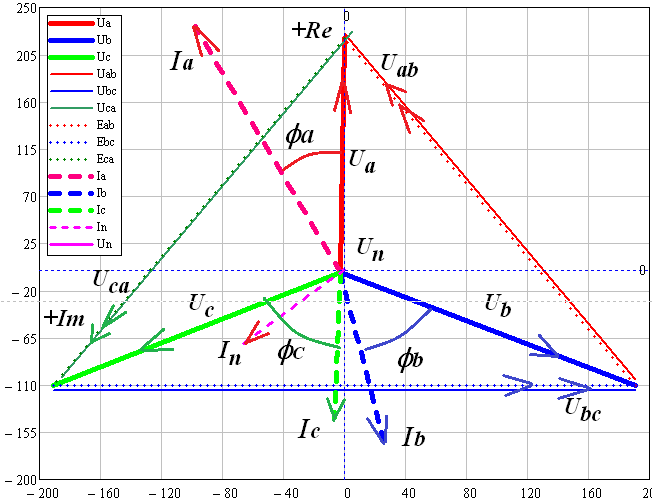 UC и UA отстают от IC по фазе, UC и UA отстают от IC по фазе,следовательно, нагрузка тут активно-ёмкостная; UB опережает IB, а нагрузка на этих фазах активно- индуктивная; фазные U примерно одинаковые; углы сдвигов фаз различны; линейные U одинаковы. UN относительно других U очень мал, поэтому его не видно на диаграмме. 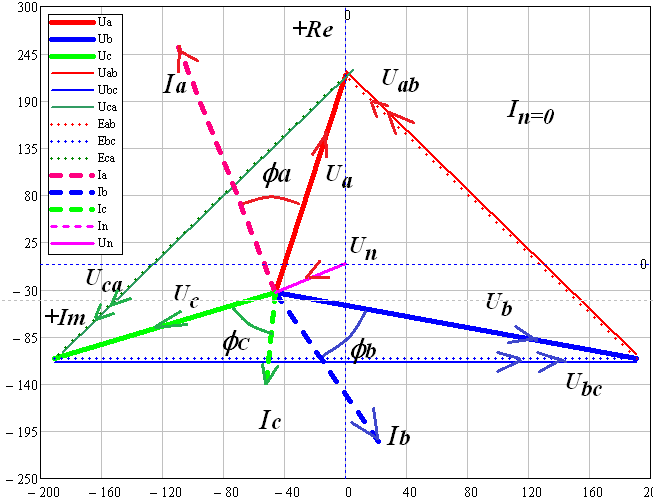 Несимметричная нагрузка (KN = 0) Несимметричная нагрузка (KN = 0)Без нейтрального провода все выводы аналогичны; кроме того, что фазные U сильно различаются → напряжение смещения нейтрали приобретает большую величину, что может вызвать сбои в работе приборов → нейтральный провод необходим; также отсутствует ток на нейтральном проводе. 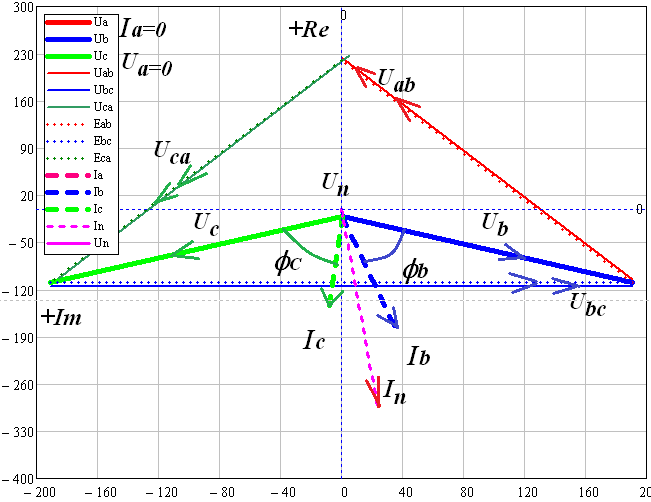 Обрыв фазы (KN = 1) Обрыв фазы (KN = 1)UC отстает от IC по фазе, нагрузка - активно-емкостная; UВ опережает IВ по фазе, нагрузка - активно-индуктивная; IA = 0, UA = 0; UB ≈ UC; Углы сдвигов фаз различны; линейные U одинаковы. 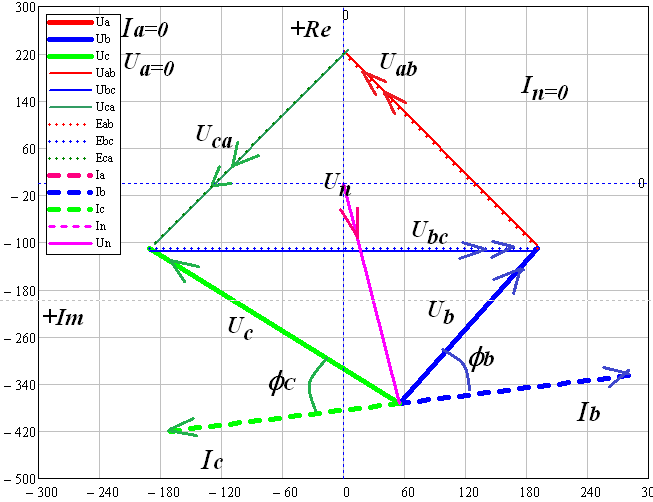 Обрыв фазы (KN = 0) Обрыв фазы (KN = 0)UC отстает от IC по фазе, нагрузка - активно-емкостная; UВ опережает IВ по фазе, нагрузка - активно-индуктивная; IA = 0, UA = 0, IN = 0; IB = IC; UB ≠ UC → необходим KN; Углы сдвигов фаз различны; линейные U одинаковы. 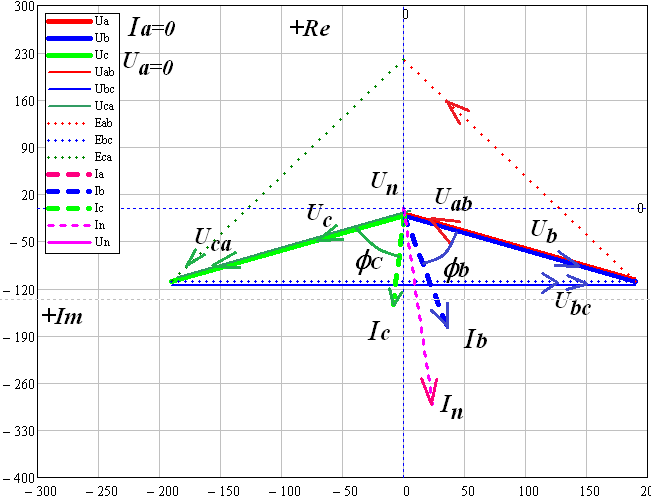 Обрыв линии (KN = 1) Обрыв линии (KN = 1)UC отстает от IC по фазе, нагрузка - активно-емкостная; UВ опережает IВ по фазе, нагрузка - активно-индуктивная; IA = 0, UA = 0; UAB ≈ UCA, UAB ≠ UBC; UB ≈ UC; UAB = UB; UCA = UC; Углы сдвигов фаз различны. UN относительно других U очень мал, поэтому его не видно на диаграмме. 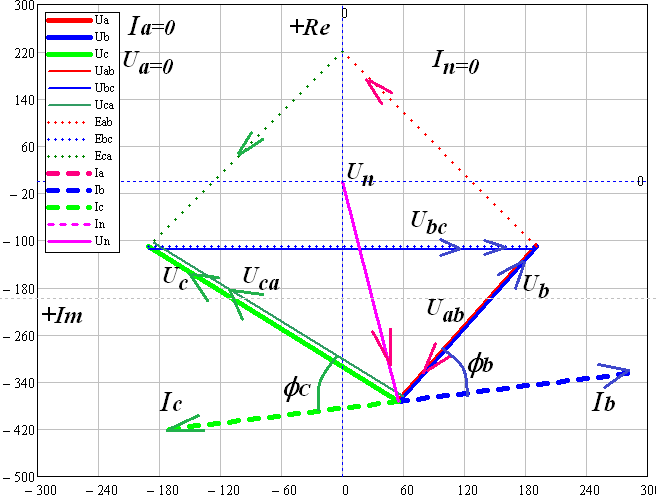 Обрыв линии (KN = 0) UC отстает от IC по фазе, нагрузка - активно-емкостная; UВ опережает IВ по фазе, нагрузка - активно-индуктивная; IA = 0, UA = 0; UAB ≠ UBC; UAB = UB; UCA = UC; UB ≠ UC → необходим KN; Углы сдвигов фаз различны; Линейные U различны. 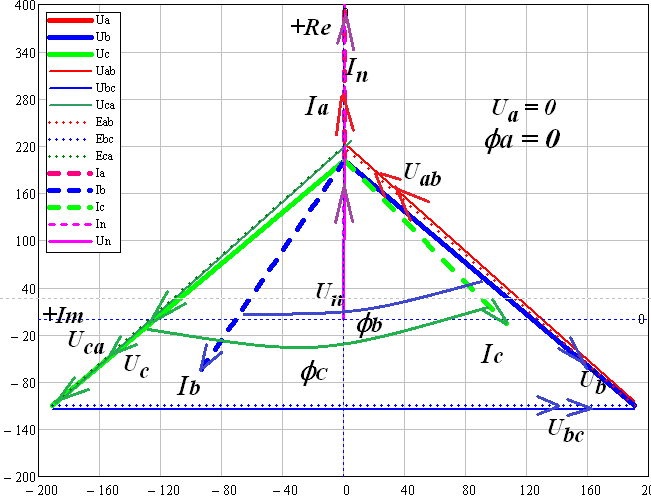 Короткое замыкание (KN = 1) Короткое замыкание (KN = 1)UC отстает от IC по фазе, нагрузка - активно-емкостная; UВ опережает IВ по фазе, нагрузка - активно-индуктивная; UA = 0; UB = UC углы сдвигов фаз различны линейные U одинаковы. 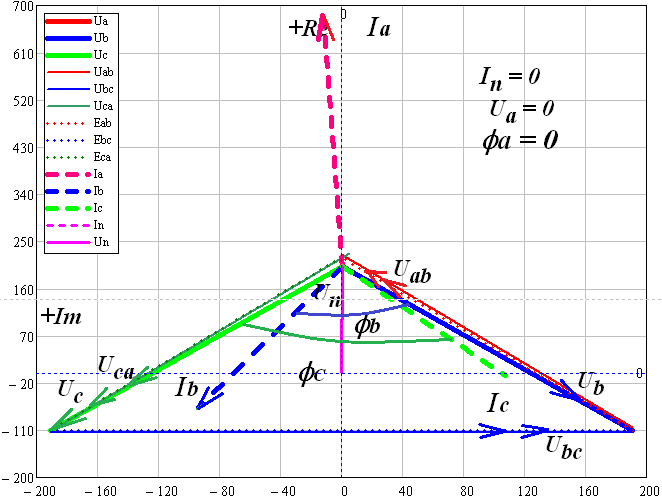 Короткое замыкание (KN = 0) Короткое замыкание (KN = 0)UС отстает от IС по фазе, нагрузка - активно-емкостная; UВ опережает IВ по фазе, нагрузка - активно-индуктивная; углы сдвигов фаз различны; линейные U одинаковы; UN при KN = 1 и при KN = 0 равны; IN = 0; UB = UC UA должна равняться нулю!, но в расчете маткада возникла ошибка. Выводы: При симметричной системе напряжений и симметричной нагрузке, когда ZA = ZB = ZC, т.е. когда RA = RB = RC = Rф и XA = XB = XC = Xф, фазные токи равны по значению и углы сдвига фаз одинаковы: IA = IB = IC = IФ = 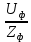 и φA = φB = φC = φф = и φA = φB = φC = φф = 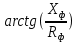 . Из векторной диаграммы токов для симметричного приемника: IA + IB + IC = 0 (геометрическая сумма трех векторов тока равна нулю). Следовательно, в случае симметричной нагрузки ток в нейтральном проводе IN = 0, поэтому необходимость в нейтральном проводе отпадает. . Из векторной диаграммы токов для симметричного приемника: IA + IB + IC = 0 (геометрическая сумма трех векторов тока равна нулю). Следовательно, в случае симметричной нагрузки ток в нейтральном проводе IN = 0, поэтому необходимость в нейтральном проводе отпадает.При симметричной системе напряжений и несимметричной нагрузке, когда ZA ≠ ZB ≠ ZC, φA ≠ φB ≠ φC токи в фазах потребителя различны и определяются по закону Ома: IA = UA / ZA; IB = UB / ZB; IC = UC / ZC. Ток в нейтральном проводе IN равен геометрической сумме фазных токов: IN = IA + IB + IC. При симметричной системе напряжений (UA = UB = UC = Uф) и симметричной нагрузке (IA + IB + IC = Iф; φA = φB = φC = φф) фазные мощности равны: P = PA + PB + PC = Pф = UфIфcosφ; Q = QA + QB + QC = UфIфsinφ Нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке. Следовательно, нейтральный провод необходим для того, чтобы выравнивать фазные напряжения приемника при несимметричной нагрузке В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз: P = PA + PB + PC Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз: Q = QA + QB + QC. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
