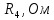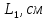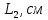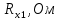Лаб_Опред.неизвест.сопр.В_(R=)чистый. Лабораторная работа (42
 Скачать 261.01 Kb. Скачать 261.01 Kb.
|
|
Лабораторная работа (42 вариант) Определение неизвестных сопротивлений при помощи мостовой схемы Цель работы: изучение законов постоянного тока. Теоретическая часть В 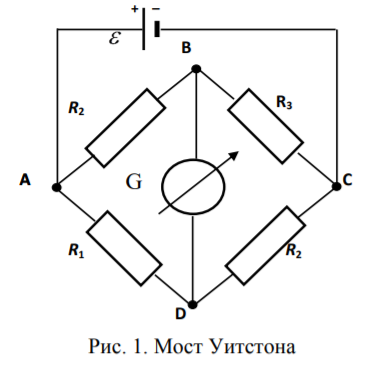 технике измерений электрическим мостом называют электрический прибор для измерения сопротивлений, емкостей, индуктивностей и других электрических величин, представляющих собой измерительную мостовую цепь, действие которой основано на методике сравнения измеряемой величины с образцовой мерой. Мостовые схемы используют индикатор баланса для сравнения двух напряжений, точно так же как и лабораторные весы сравнивают две массы и указывают на то, что они равны. В отличие от «потенциометрических» схем, используемых для простого измерения неизвестного напряжения, мостовые схемы могут использоваться для измерения всех видов электрических величин, в том числе и сопротивлений с высокой точностью. Стандартная мостовая схема, часто называемая мостом Уитстона (Wheatstone bridge), изображена на рис. 1. технике измерений электрическим мостом называют электрический прибор для измерения сопротивлений, емкостей, индуктивностей и других электрических величин, представляющих собой измерительную мостовую цепь, действие которой основано на методике сравнения измеряемой величины с образцовой мерой. Мостовые схемы используют индикатор баланса для сравнения двух напряжений, точно так же как и лабораторные весы сравнивают две массы и указывают на то, что они равны. В отличие от «потенциометрических» схем, используемых для простого измерения неизвестного напряжения, мостовые схемы могут использоваться для измерения всех видов электрических величин, в том числе и сопротивлений с высокой точностью. Стандартная мостовая схема, часто называемая мостом Уитстона (Wheatstone bridge), изображена на рис. 1.Классическая мостовая цепь состоит из четырех сопротивлений 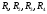 , соединенных последовательно в виде четырехугольника (рис. 1), причем точки А, В, C, D называют вершинами. Ветвь AC, содержащая источник питания , соединенных последовательно в виде четырехугольника (рис. 1), причем точки А, В, C, D называют вершинами. Ветвь AC, содержащая источник питания 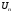 , называется диагональю питания, а ветвь BD, содержащая сопротивление нагрузки , называется диагональю питания, а ветвь BD, содержащая сопротивление нагрузки 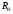 , – диагональю нагрузки. Сопротивления , – диагональю нагрузки. Сопротивления 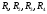 , включенные между двумя соседними вершинами, называются плечами мостовой цепи. , включенные между двумя соседними вершинами, называются плечами мостовой цепи. Название «мостовая цепь» объясняется тем, что диагонали, как мостики, соединяют две противолежащие вершины (диагональ нагрузки, например, ранее так и называлась – мост). Схема, представленная на рис. 1, известна в литературе как четырехплечный мост, или мост Уитстона. В данной лабораторной работе используется одна из разновидностей моста Уитстона, которая позволяет проводить измерения величин активных сопротивлений. Мосты Уитстона считаются превосходным средством измерения сопротивления среди схем различных омметров. В отличие от нелинейных схем, имеющих нелинейные шкалы, и связанные с этим погрешности измерений, мостовая схема является линейной и довольно точной. Математика описания её работы основана на простых отношениях и пропорциях. Имея стандартные сопротивления достаточной точности и нульдетектор с необходимой чувствительностью, достижимая точность измерения сопротивления может быть не хуже ± 0,05 % при использовании моста Уитстона. Это метод измерения сопротивления предпочитают использовать в калибровочных лабораториях из-за его высокой точности. Существует много вариаций основной схемы моста Уитстона. Большинство мостов постоянного тока используются для измерения сопротивления, в то время как мосты переменного тока могут быть использованы для измерения различных электрических величин, таких как индуктивность, ёмкость и частота. Так, например, мост Уитстона используется для определения изменения сопротивления тензорезистора (тензодатчика), «измеряющего» изменение давления, температуры, распределение деформаций (изгиб или сжатие-растяжение) в конструктивных элементах зданий, сооружений, в сводах подземных выработок и многое другое. Причем, из-за высокой чувствительности мостика к дисбалансировке, тензочувствительность датчиков также высока, что способствует измерению даже микродислокаций (микродавлений и т.п.) в исследуемом объекте. Условие равновесия моста Уитстона Основной электрической характеристикой проводника является его сопротивление. Сопротивление представляет собой меру противодействия установлению в проводнике электрического тока. Зависит сопротивление проводника от его геометрии и электрических свойств его материала. Проводник длиной l с постоянным сечением S обладает сопротивлением R: 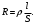 Здесь r – зависящая от материала проводника и его состояния величина, называемая удельным сопротивлением. В настоящей работе для измерения сопротивлений использован линейный мост Уитстона. Электрическая схема моста представлена на рис. 2. В мост включены: известное сопротивление 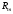 , неизвестное сопротивление , неизвестное сопротивление  , реохорд или аналогичная система, имеющая однородный участок АС с постоянным по всей длине удельным сопротивлением. , реохорд или аналогичная система, имеющая однородный участок АС с постоянным по всей длине удельным сопротивлением.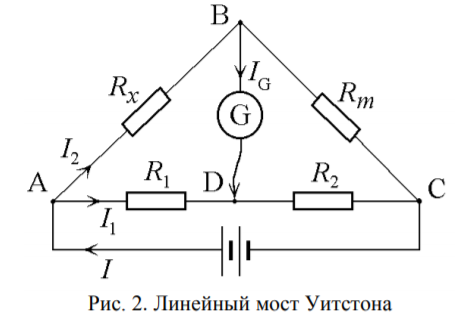 При произвольных значениях сопротивлений через гальванометр G будет течь ток того или иного направления. Однако сопротивления можно подобрать таким образом, что ток в гальванометре ответвляться не будет ( 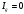 ). В этом случае потенциалы точек B и D будут равны ( ). В этом случае потенциалы точек B и D будут равны (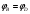 ). Такое состояние называют равновесием моста. ). Такое состояние называют равновесием моста. Установим зависимость, которая существует между сопротивлениями 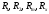 в этот момент. в этот момент.По первому правилу Кирхгофа 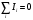 в точке B и D сумма токов равна нулю, т.е. при условии в точке B и D сумма токов равна нулю, т.е. при условии 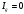 получаем равенство токов: получаем равенство токов: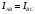 и и 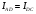 . . По второму правилу Кирхгофа 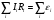 для контуров ABDA и BCDB можно записать: для контуров ABDA и BCDB можно записать: 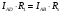 , , 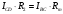 Из последних уравнений вытекает соотношение: 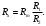 Сопротивления 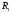 и и 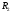 для линейной схемы моста Уитстона лежат на одной прямой AC, называемой реохордом, и представляют собой однородную проволоку (струну), по которой на скользящем контакте перемещается движок D, соединенный с гальванометром G. Вследствие того, что проволока реохорда однородна и тщательно откалибрована (имеет везде одинаковое поперечное сечение), отношение сопротивлений участков цепи AD (сопротивление для линейной схемы моста Уитстона лежат на одной прямой AC, называемой реохордом, и представляют собой однородную проволоку (струну), по которой на скользящем контакте перемещается движок D, соединенный с гальванометром G. Вследствие того, что проволока реохорда однородна и тщательно откалибрована (имеет везде одинаковое поперечное сечение), отношение сопротивлений участков цепи AD (сопротивление 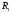 ) и DC (сопротивление ) и DC (сопротивление 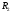 ) можно заменить отношением соответствующих длин плеч реохорда ) можно заменить отношением соответствующих длин плеч реохорда 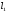 и и 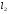 (на основании прямо пропорциональной зависимости (на основании прямо пропорциональной зависимости 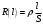 ): ): 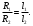 Тогда окончательная формула для определения искомого сопротивления имеет вид: 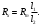 И 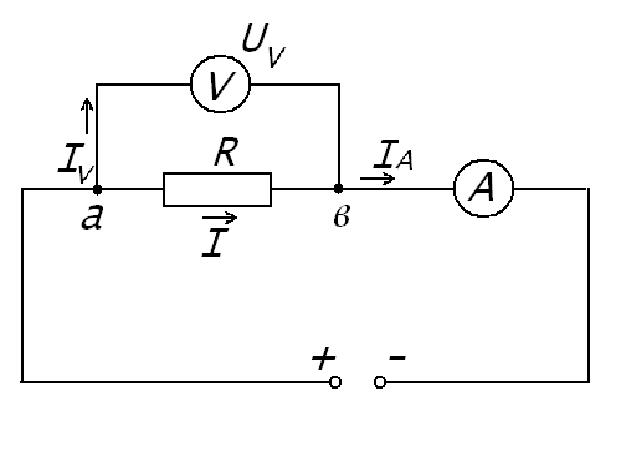 змерение сопротивлений змерение сопротивленийРис. 3. Наиболее простой способ определения сопротивлений основан на измерении силы тока при помощи амперметра и напряжения – при помощи вольтметра (рис. 3). Если амперметр показывает силу тока в амперах (I), а вольтметр – напряжение на концах проводника в вольтах (U), то сопротивление проводника в омах равно 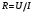 . При этом должно соблюдаться условие . При этом должно соблюдаться условие 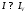 . Точность этого метода определяется приборной погрешностью вольтметра и амперметра. Для точного определения сопротивлений используют метод сравнения сопротивлений, не требующий измерения тока и напряжения. Этот метод осуществляется по схеме моста, изображенного на рис.2. Электрическая мостовая схема служит для определения электрического сопротивления. Четыре сопротивления . Точность этого метода определяется приборной погрешностью вольтметра и амперметра. Для точного определения сопротивлений используют метод сравнения сопротивлений, не требующий измерения тока и напряжения. Этот метод осуществляется по схеме моста, изображенного на рис.2. Электрическая мостовая схема служит для определения электрического сопротивления. Четыре сопротивления 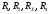 составляют замкнутый четырёхугольник АВСD. Противолежащие вершины четырёхугольника соединяются диагоналями. В одну диагональ, между точками С и D, подключается гальванометр G, в другую – батарея e через ключ Кл. составляют замкнутый четырёхугольник АВСD. Противолежащие вершины четырёхугольника соединяются диагоналями. В одну диагональ, между точками С и D, подключается гальванометр G, в другую – батарея e через ключ Кл.Так как потенциалы точек В и D равны, значения падения напряжения на участках АВ и АD и участках ВС и DС тоже будут равны; т.е. 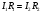 , ,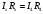 . Измерительный мост в этом случае оказывается сбалансированным. Полученные равенства разделим почленно и, принимая во внимание, что . Измерительный мост в этом случае оказывается сбалансированным. Полученные равенства разделим почленно и, принимая во внимание, что 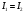 а а 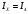 , получим: , получим: 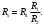 Таким образом, зная сопротивление одного проводника, например, Таким образом, зная сопротивление одного проводника, например, 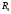 и отношение сопротивлений двух других проводников, можно определить сопротивление четвёртого проводника. Заменяя сопротивления и отношение сопротивлений двух других проводников, можно определить сопротивление четвёртого проводника. Заменяя сопротивления 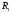 и и 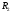 длинами плеч длинами плеч 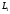 и и 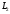 , получим рабочую формулу для определения неизвестного сопротивления: , получим рабочую формулу для определения неизвестного сопротивления: 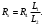 (2) (2)Описание экспериментальной установки Мост Уитстона реализован в виртуальной лабораторной установке (рис. 4, рис. 3), состоит из сопротивлений 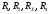 , которые соединены между собой таким образом, что образуют замкнутый четырехугольник. Два противоположных угла четырехугольника соединяются с батареей (Е = 25 В) через ключ К, а два других угла – через гальванометр G. Сопротивления , которые соединены между собой таким образом, что образуют замкнутый четырехугольник. Два противоположных угла четырехугольника соединяются с батареей (Е = 25 В) через ключ К, а два других угла – через гальванометр G. Сопротивления 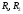 соответствуют сопротивлению проволоки реохорда, т.е. плечам соответствуют сопротивлению проволоки реохорда, т.е. плечам 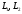 реохорда [запишите рабочую формулу (2)]. Длину плеч можно изменить при помощи кнопки-движка “RHEOHORD CONTROOL”. реохорда [запишите рабочую формулу (2)]. Длину плеч можно изменить при помощи кнопки-движка “RHEOHORD CONTROOL”.Сопротивление 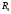 представляет собой магазин сопротивлений, позволяющий набрать любое сопротивление в пределах от представляет собой магазин сопротивлений, позволяющий набрать любое сопротивление в пределах от 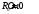 до до 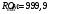 . Неизвестное сопротивление на схеме обозначено цифрами 1 или 2. Нажимая на кнопку неизвестного сопротивления, можно получить в схеме неизвестные сопротивления 1 . Неизвестное сопротивление на схеме обозначено цифрами 1 или 2. Нажимая на кнопку неизвестного сопротивления, можно получить в схеме неизвестные сопротивления 1 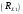 или 2 или 2 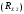 , а также их последовательное , а также их последовательное 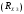 и параллельное и параллельное 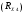 включение. Когда источник тока замкнут, то через «плечи» моста пойдет ток и гальванометр покажет этот ток. включение. Когда источник тока замкнут, то через «плечи» моста пойдет ток и гальванометр покажет этот ток.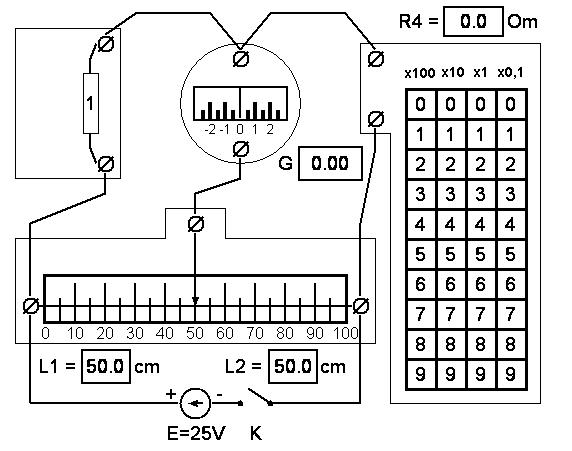 Рис.4. Схема виртуальной лабораторной установки При помощи кнопки-движка «RHEOHORD CONTROOL» можно добиться такого положения контакта D на реохорде, когда ток через гальванометр будет равен нулю и окажется справедливым соотношение (2). То же самое можно сделать подбором сопротивления 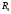 , не изменяя соотношение плеч , не изменяя соотношение плеч 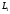 , , 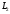 реохорда. реохорда.Рабочие формулы 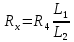 – определение неизвестного сопротивления – определение неизвестного сопротивления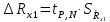 , где , где 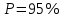 - доверительная вероятность, - доверительная вероятность, 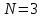 - число опытов, - число опытов, 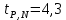 , , 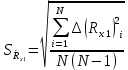 - расчет - расчет 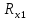 с учетом доверительных погрешностей (коэффициента Стьюдента) с учетом доверительных погрешностей (коэффициента Стьюдента)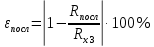 - вычисление относительной ошибки измерений при последовательном соединении - вычисление относительной ошибки измерений при последовательном соединении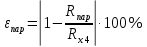 - вычисление относительной ошибки измерений при параллельном соединении - вычисление относительной ошибки измерений при параллельном соединенииЭкспериментальная часть Произведем необходимые нам для эксперимента измерения и вычисления запишем в таблицу 1. Таблица 1. Измерений и вычислений
Вычислим неизвестное сопротивление по формуле: 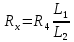 . Для этого произведем необходимые нам измерения и вычисления: . Для этого произведем необходимые нам измерения и вычисления:Дано: 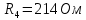 . Произведем измерения длин плеч . Произведем измерения длин плеч 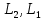 . Затем увеличим . Затем увеличим 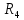 на 20%, на 20%, 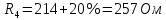 и произведем измерения. Также уменьшим и произведем измерения. Также уменьшим 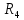 на 20%, на 20%, 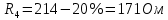 и произведем измерения. Запишем результаты в табл.1. и произведем измерения. Запишем результаты в табл.1. Вычислим неизвестное сопротивление 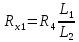 : :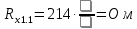 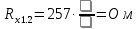 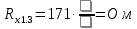 Вычислим среднее значение 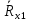 : :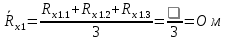 Вычислим абсолютную погрешность 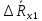 : : 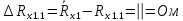 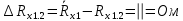 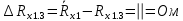 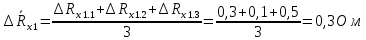 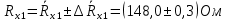 - с учетом абсолютной погрешности - с учетом абсолютной погрешностиРассчитаем 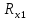 с учетом доверительных погрешностей (коэффициента Стьюдента): с учетом доверительных погрешностей (коэффициента Стьюдента):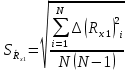 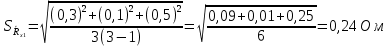 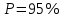 - доверительная вероятность, - доверительная вероятность, 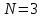 - число опытов, - число опытов,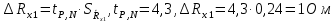 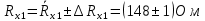 Неизвестное сопротивление с учетом доверительной погрешности: 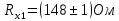 Вычислим неизвестное сопротивление 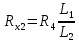 : :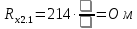 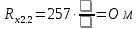 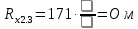 Вычислим среднее значение 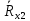 : :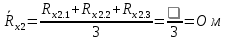 Вычислим абсолютную погрешность 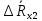 : : 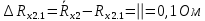 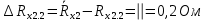 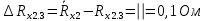 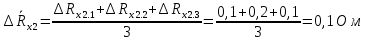 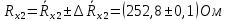 - с учетом абсолютной погрешности - с учетом абсолютной погрешностиРассчитаем 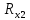 с учетом доверительных погрешностей (коэффициента Стьюдента): с учетом доверительных погрешностей (коэффициента Стьюдента):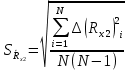 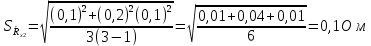 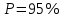 - доверительная вероятность, - доверительная вероятность, 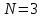 - число опытов, - число опытов,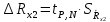 , , 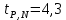 , , 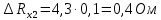 , тогда , тогда 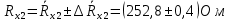 Неизвестное сопротивление с учетом доверительной погрешности: 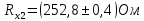 Вычислим 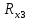 при последовательном соединении неизвестных сопротивлений: при последовательном соединении неизвестных сопротивлений: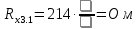 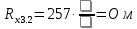 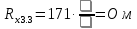 Вычислим среднее значение 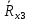 : :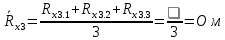 Вычислим абсолютную погрешность 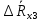 : : 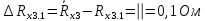 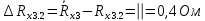 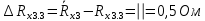 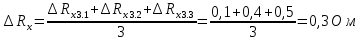 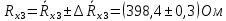 - с учетом абсолютной погрешности - с учетом абсолютной погрешностиРассчитаем 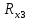 с учетом доверительных погрешностей (коэффициента Стьюдента): с учетом доверительных погрешностей (коэффициента Стьюдента):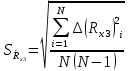 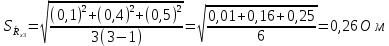 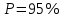 - доверительная вероятность, - доверительная вероятность, 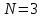 - число опытов, - число опытов,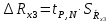 , , 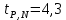 , , 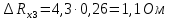 , тогда , тогда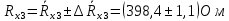 Неизвестное сопротивление с учетом доверительной погрешности: 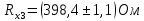 Вычислим 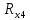 при параллельном соединении неизвестных сопротивлений: при параллельном соединении неизвестных сопротивлений: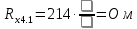 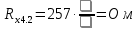 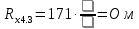 Вычислим среднее значение 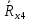 : :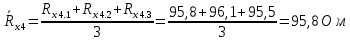 Вычислим абсолютную погрешность 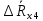 : : 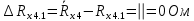 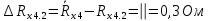 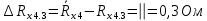 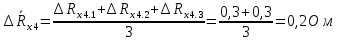 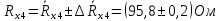 - с учетом абсолютной погрешности - с учетом абсолютной погрешностиРассчитаем 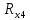 с учетом доверительных погрешностей (коэффициента Стьюдента): с учетом доверительных погрешностей (коэффициента Стьюдента):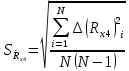 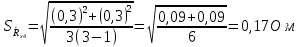 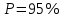 - доверительная вероятность, - доверительная вероятность, 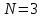 - число опытов, - число опытов,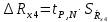 , , 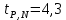 , , 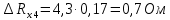 , тогда , тогда 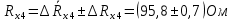 Неизвестное сопротивление с учетом доверительной погрешности: 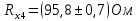 Проверим экспериментальные значения и теоретические: При последовательном соединении: 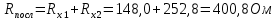 - получено теоретически - получено теоретически 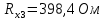 - получено с помощью лабораторной установки - получено с помощью лабораторной установкиОтносительная ошибка измерения последовательного соединения сопротивлений: 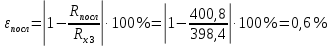 При параллельном соединении: 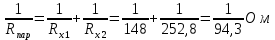 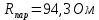 - получено теоретически - получено теоретически 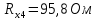 - получено с помощью лабораторной установки - получено с помощью лабораторной установкиОтносительная ошибка измерения параллельного соединения сопротивлений: 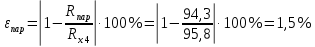 Вывод: изучили законы постоянного тока на примере установки «Мост Уитстона», которая позволяет с высокой точностью определить неизвестное сопротивление, и подтверждает справедливость закона Ома. Полученные лабораторным способом измерения сравнили с теоретическими и получили относительные ошибки измерения: при последовательном соединении 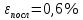 , при параллельном соединении , при параллельном соединении 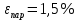 , ошибки незначительные и это еще раз доказывает высокую точность проведенного опыта с помощью Моста Уитстона. Искомые сопротивления с учетом доверительных погрешностей , ошибки незначительные и это еще раз доказывает высокую точность проведенного опыта с помощью Моста Уитстона. Искомые сопротивления с учетом доверительных погрешностей 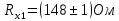 , , 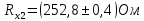 , , 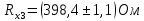 , , 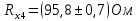 . . |