моя лаба мэт5. Лабораторная работа 5 Исследование свойств конденсаторных материалов Основные понятия и определения
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
|
Лабораторная работа № 5 Исследование свойств конденсаторных материалов Основные понятия и определения К конденсаторным материалам относят материалы, применяемые в качестве рабочего диэлектрика в конденсаторах. К основным параметрам конденсатора относят емкость С, температурный коэффициент емкости αс и тангенс угла диэлектрических потерь tg δ. Значения этих параметров во многом обусловлены свойствами используемого диэлектрического материала, основными характеристиками которого являются относительная диэлектрическая проницаемость ε и температурный коэффициент диэлектрической проницаемости αε. Относительная диэлектрическая проницаемость характеризует способность различных диэлектриков поляризоваться в электрическом поле: ε = Сд/С0, где Сд – емкость конденсатора с диэлектриком; С0 – емкость того же конденсатора в вакууме. Поляризация может быть вызвана упругим смещение и деформацией электронных оболочек под действием поля (электронная поляризация), ориентацией дипольных молекул (дипольно-релаксационная поляризация), смещением ионов (ионная и ионно- релаксационная поляризация). Электронная и ионная поляризации устанавливаются практически мгновенно. Остальные механизма поляризации относятся к замедленным видам. В процессе поляризации диэлектрик приобретает электрический момент, на его поверхностях образуются связанные заряды, на обкладках удерживается дополнительный заряд. В результате емкость конденсатора возрастает. Состояние диэлектрика, характеризующееся наличием электрического момента у любого элемента его объема, называют пояризованностью. В общем случае диэлектрическая проницаемость зависит от температуры и частоты электрического поля. Характер зависимости определяется присущими диэлектрику механизмами поляризации. При включении конденсатора под напряжение в нем наблюдаются потери электрической энергии, приводящие к его разогреванию. Потери энергии складываются из потерь в диэлектрике и потерь в проводящих частях конденсатора. Диэлектрическими потерями (потерями энергии в диэлектрике) называют электрическую мощность, затрачиваемую на нагрев диэлектрика. Находящегося в электрическом поле. Различают два основных вида диэлектрических потерь: потери на электропроводность и релаксационные потери. Потери на электропроводность обнаруживаются в диэлектриках, имеющих заметную электропроводность, объемную или поверхностную, и наблюдаются во всех диэлектриках, как на постоянном, так и на переменном напряжении, причем являются преобладающими при низких частотах и при повышенных температурах. Релаксационные потери обусловлены активными составляющими поляризационных токов. Они характерны для диэлектриков с замедленными механизмами поляризации и проявляются в области достаточно высоких частот, когда сказывается отставание поляризации от изменения поля. Полные потери в участке изоляции с емкостью С при воздействии напряжения U с угловой частотой ω Pa = U2ωCtgδ, где δ – угол диэлектрических потерь. Углом диэлектрических потерь δ называют угол, дополняющий до 90° угол сдвига фаз φ между током и напряжением в емкости цепи. В случае идеального диэлектрика вектор тока в такой цепи опережает вектор напряжения на угол π/2; при этом угол δ равен нулю. Чем больше рассеиваемая в диэлектрике мощность, тем меньше угол сдвига фаз φ и тем больше угол диэлектрических потерь δ и его функция tg δ. Параметр tg δ характеризует способность диэлектрика рассеивать энергию в электрическом поле. Он безразмерный, не зависит от формы и размеров участка изоляции, а определяется только свойствами диэлектрика. Параметр tg δ определяет диапазон частот, в котором возможно использование конденсатора с данным диэлектриком. Исходные данные
C0=15,22 пФ Обработка результатов
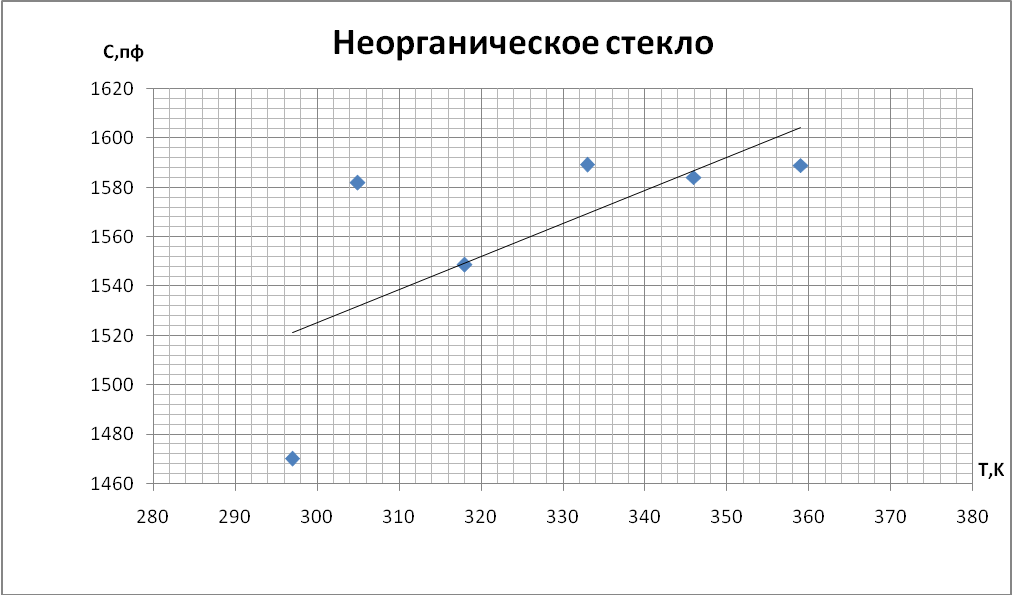 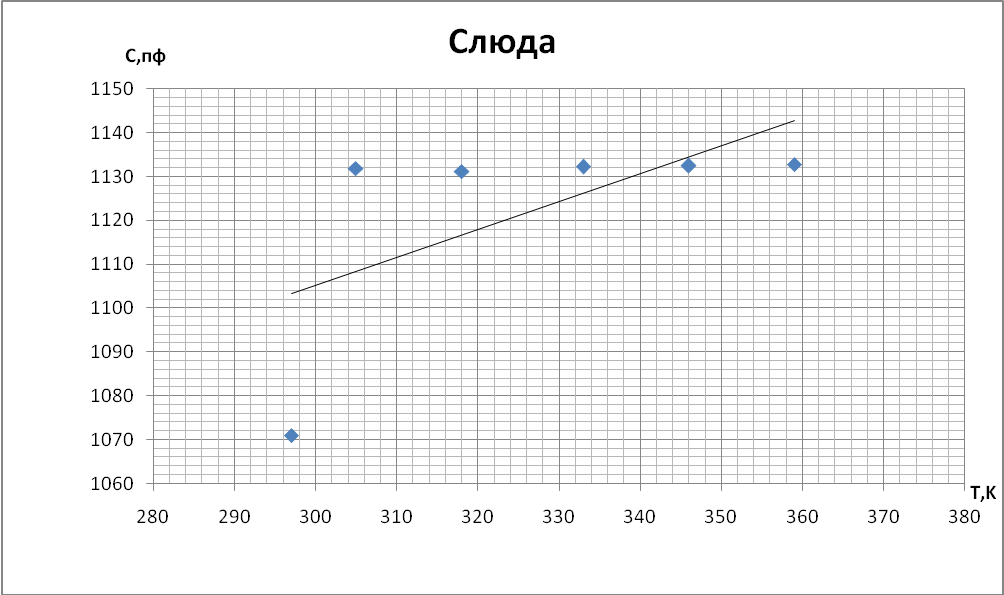 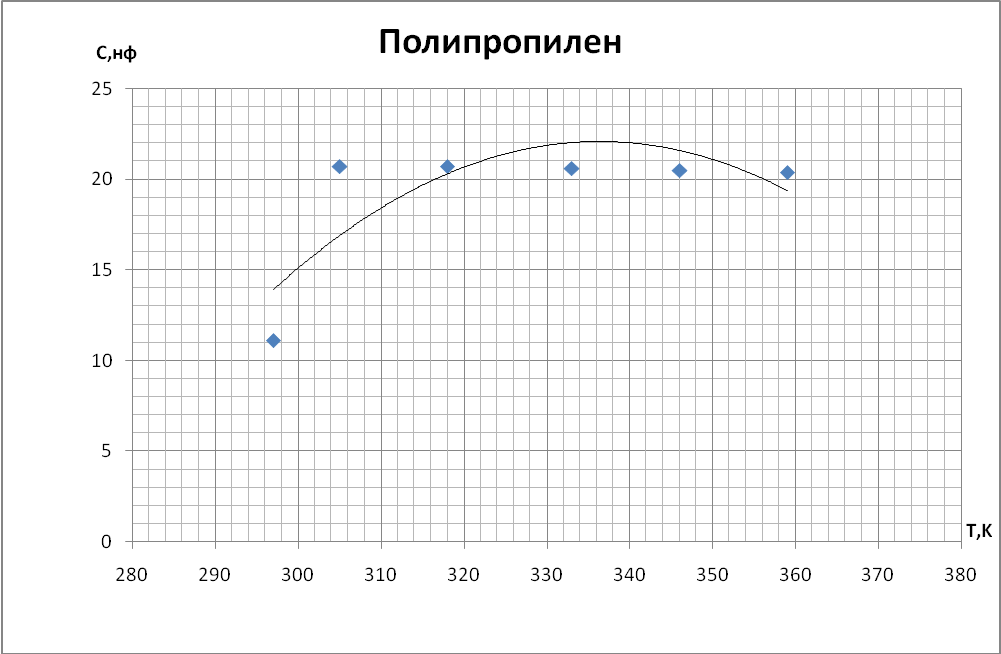 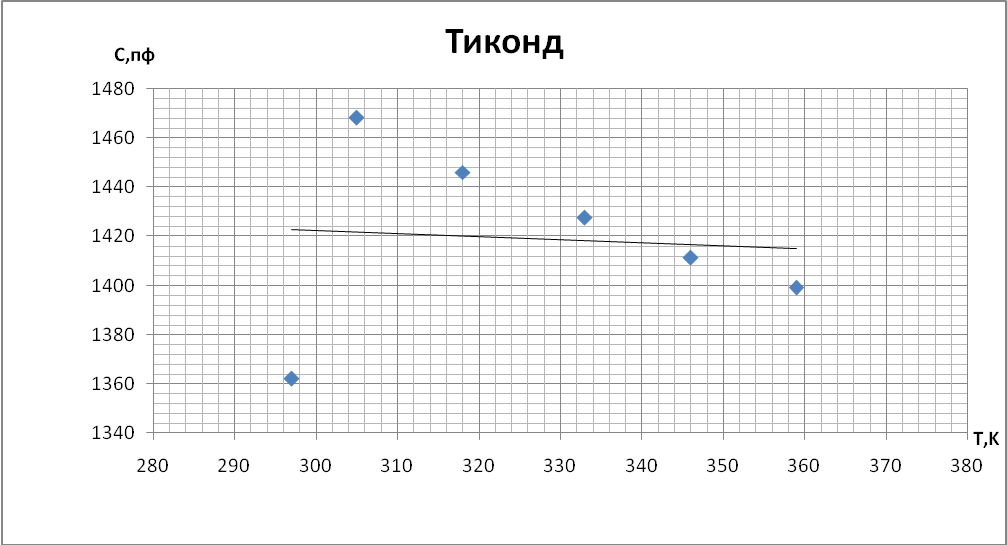 
Пример вычислений: Найдем значение производной для первого образца. В формулу линейно подставим экспериментальные данные для неорганического стекла. Получим значение коэффициента k1 = 1,3454. Найдем значение температурного коэффициента емкости для температуры 22°С (295К), С= 1,6376E-09Ф αс = 9,15E-04 К-1.
Пример вычислений: образец 1 (неорганическое стекло), Т=24°С, αс = 9,15E-04 К-1, αlд = 3,00E-06 К-1 αε = αс - αlд, αε = 0,67E-04 - 3,00E-06, αε = 9,12E-04 К-1. Значение температурного коэффициента линейного расширения диэлектрика αlд:
Таблица 5.2
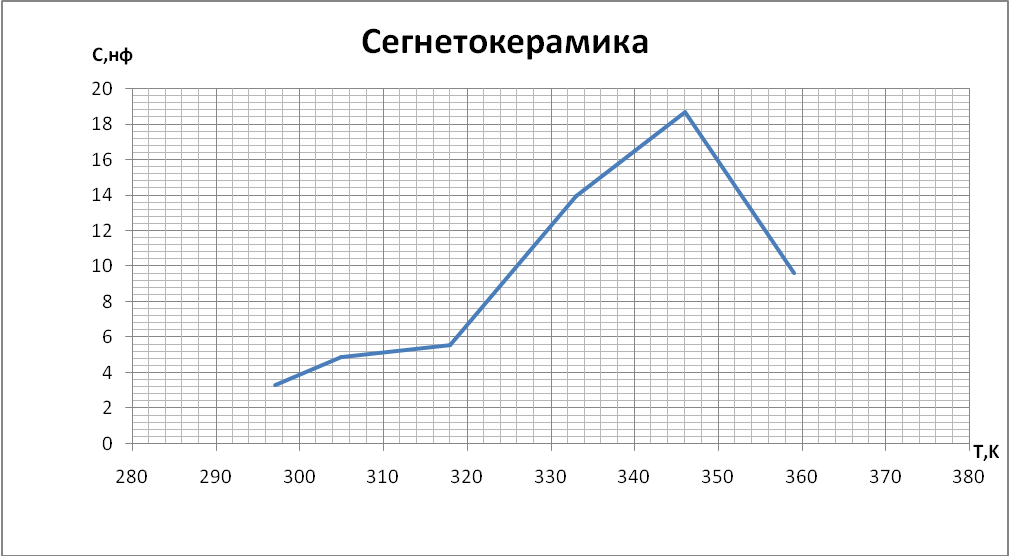
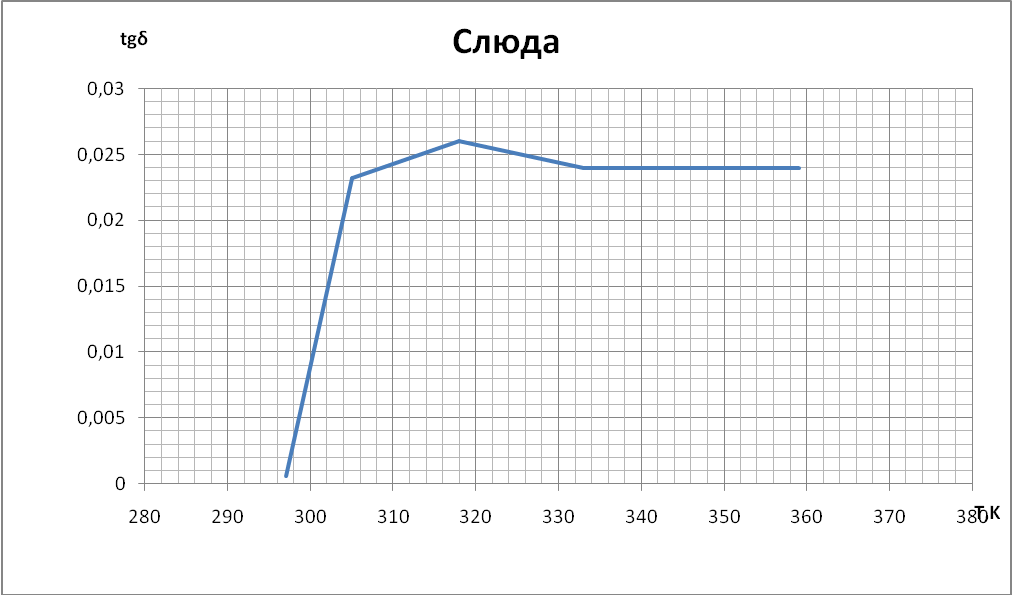
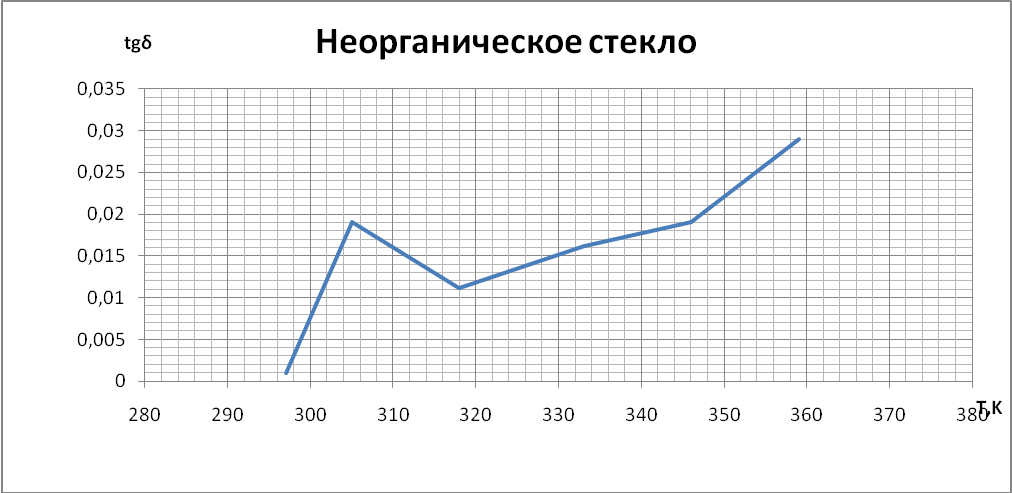
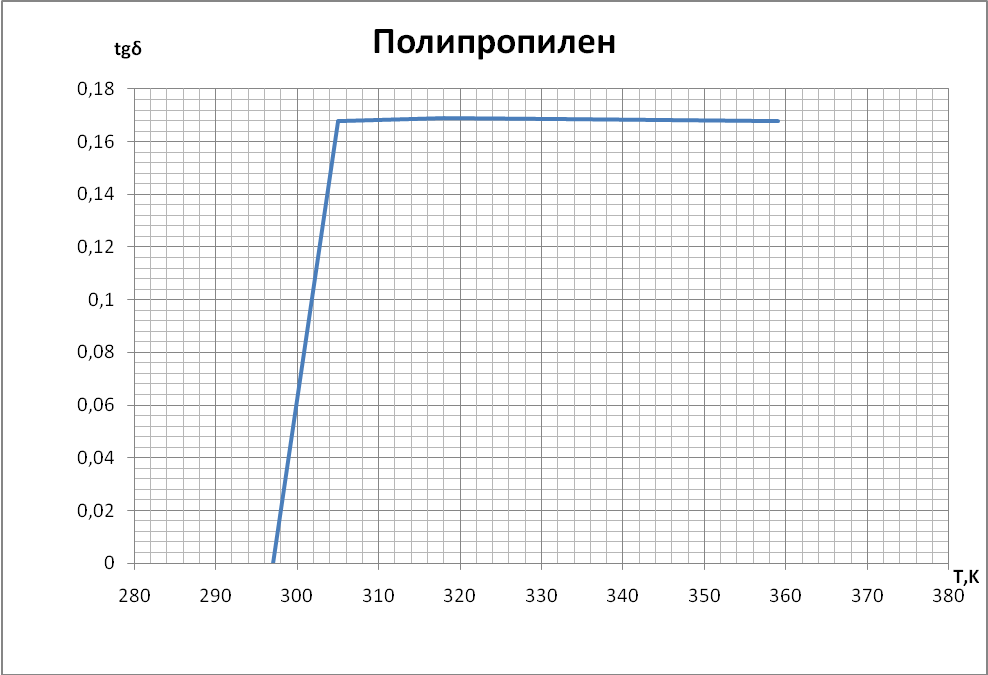
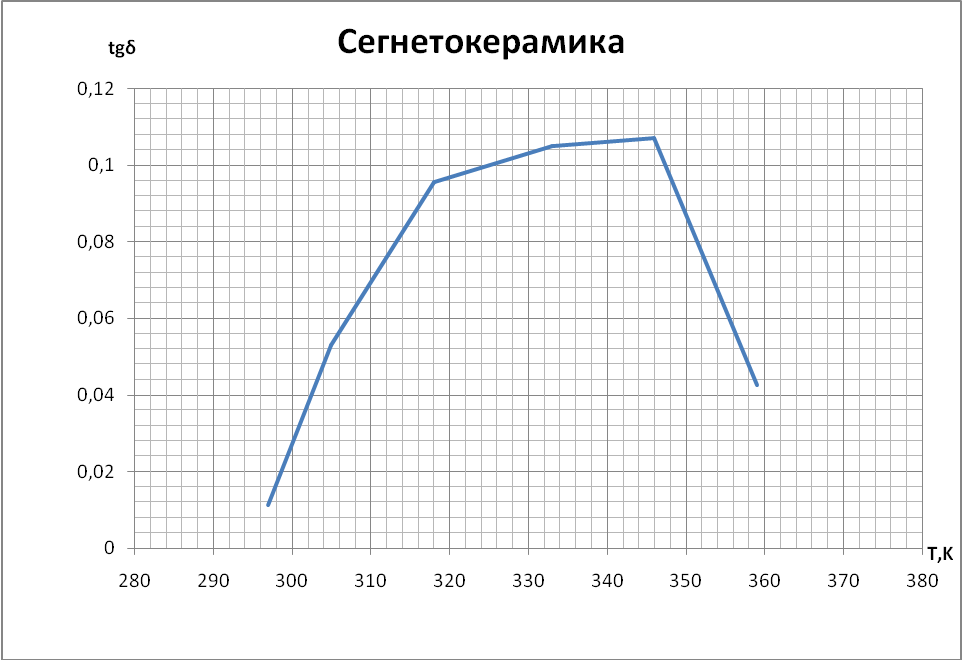
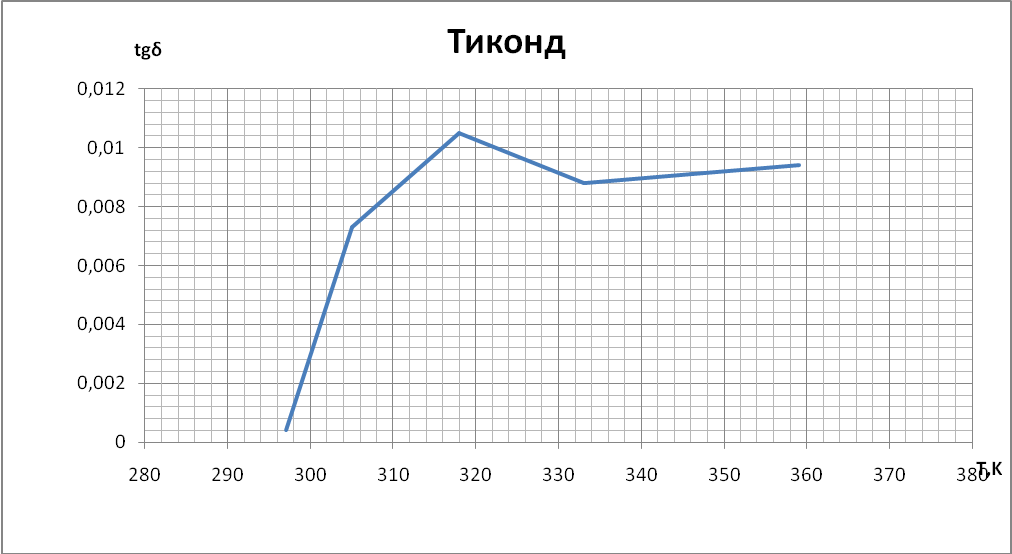
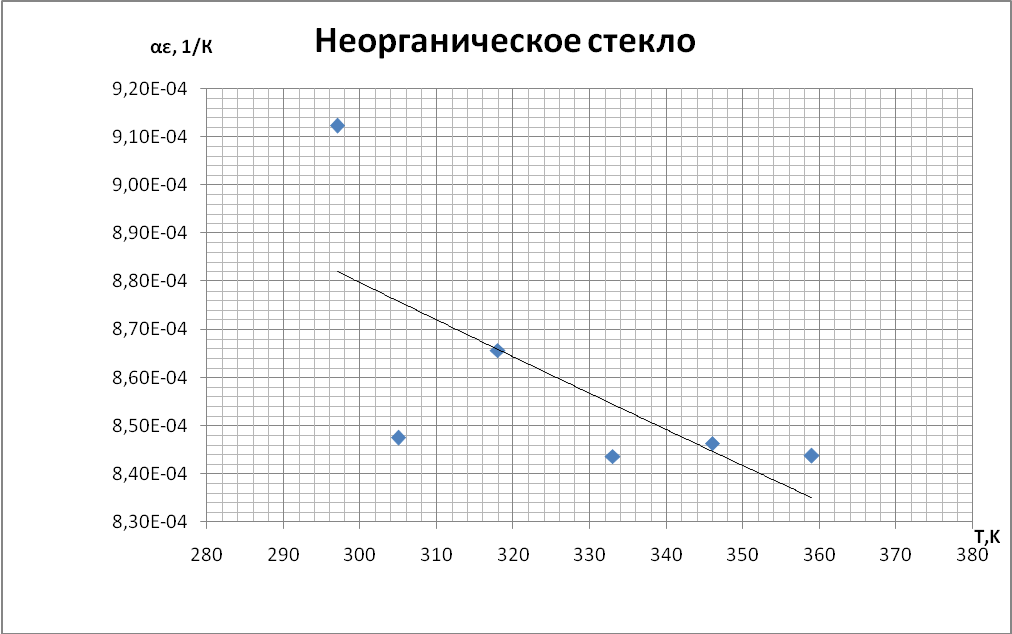 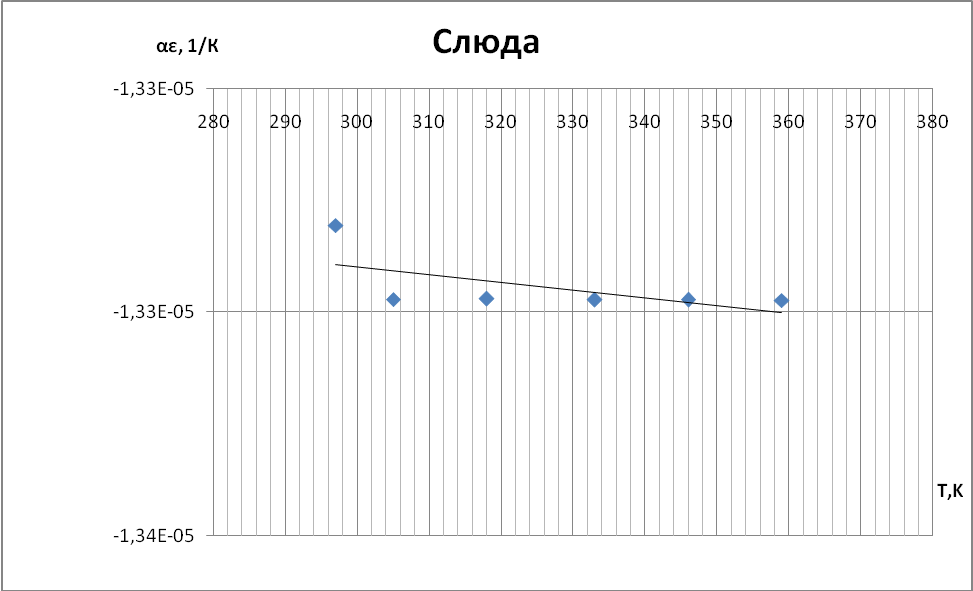 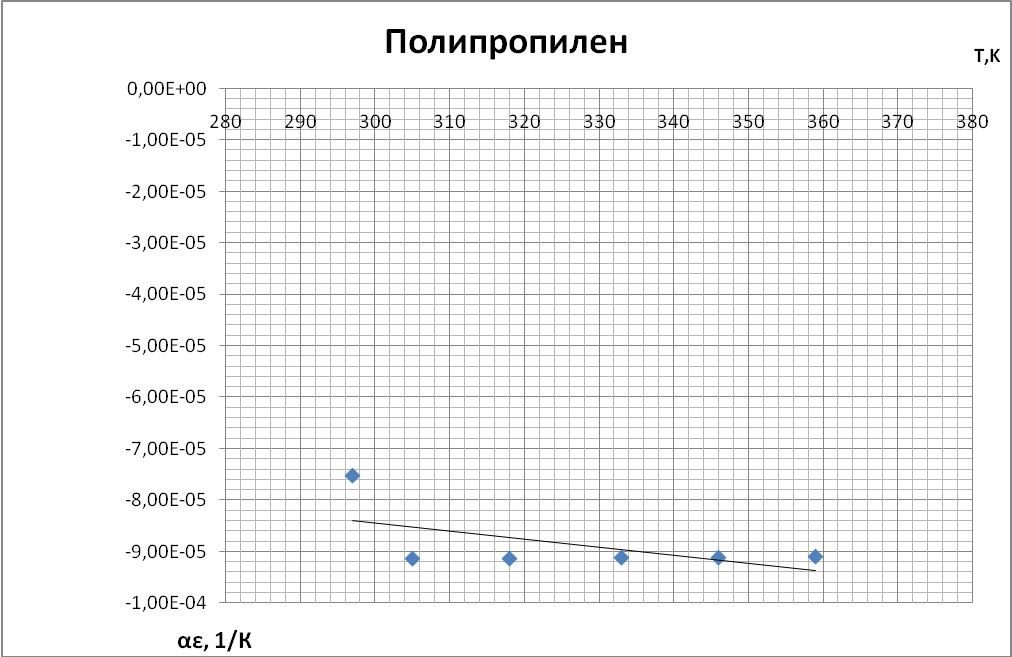 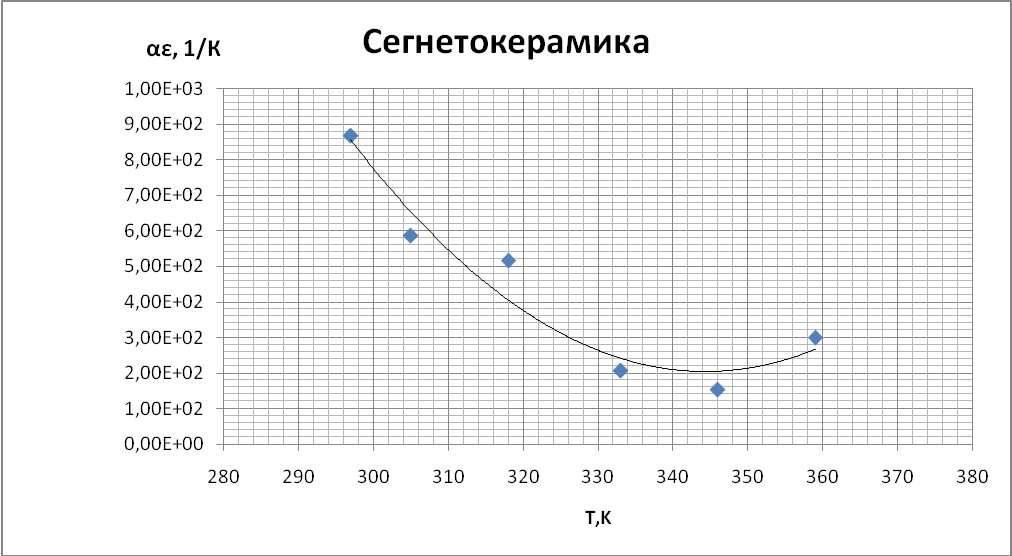 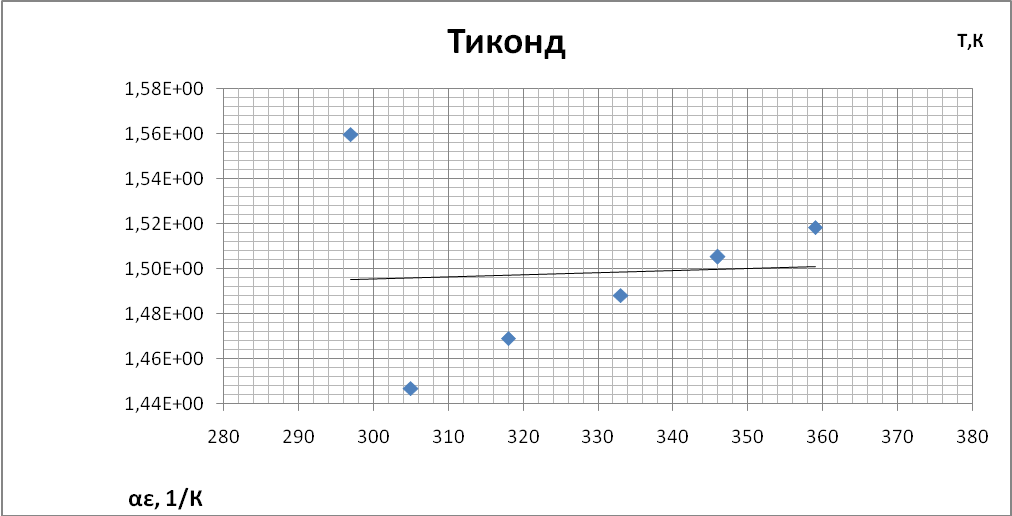 Выводы При построении графиков температурной зависимости емкости мы обнаружили, что графики для первых четырех образцов линейны: для неорганического стекла и слюды с ростом температуры увеличивается емкость. У конденсатора с полипропиленовым диэлектриком и диэлектриком из тиконда емкость немного уменьшается с ростом температуры. Совсем иначе ведет себя сегнетокерамика, емкость такого конденсатора растёт до некоторой температуры 73°С (С = 18,66 нФ), далее уменьшается т.к. уменьшается диэлектрическая проницаемость сегнетоэлектрика. При построении температурной зависимости температурного коэффициента диэлектрической проницаемости αε мы получили, что для сегнетокерамики, неорганического стекла и тиконда данный коэффициент положителен. Для слюды и полипропилена αε имеет отрицательное значение. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
