Лабораторныая работа 5. Лабораторная работа_05. Лабораторная работа 5 Измерение параметров вращательного движения
 Скачать 288 Kb. Скачать 288 Kb.
|
|
Лабораторная работа №5 Измерение параметров вращательного движения Цель работы: измерить параметры, характеризующие вращательное движения –момент силы, угловое ускорение и момент инерции с помощью маятника Обербека МЕТОДИКА ЭКСПЕРИМЕНТАВ данной работе используется установка, называемая маятником Обербека. Она позволяет изучать вращательное движение при различных значениях момента внешних сил и момента инерции системы. М 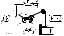 аятник Обербека состоит из четырех одинаковых спиц, укрепленных на втулке под прямым углом друг к другу (рис.1). На спицах могут быть укреплены одинаковые по форме и массе грузы (обычно грузы имеют форму цилиндров). На втулке намотана нить, которая перекинута через неподвижный блок. На конце нити можно укреплять гири известной массы. аятник Обербека состоит из четырех одинаковых спиц, укрепленных на втулке под прямым углом друг к другу (рис.1). На спицах могут быть укреплены одинаковые по форме и массе грузы (обычно грузы имеют форму цилиндров). На втулке намотана нить, которая перекинута через неподвижный блок. На конце нити можно укреплять гири известной массы.Под действием момента силы натяжения нити T вся система равноускоренно вращается вокруг горизонтальной оси Z с угловым ускорением . Силу натяжения нити можно варьировать, изменяя массу укрепленных на нити гирь. Величина углового ускорения зависит также от значения момента инерции системы относительно оси вращения (оси Z). 1. В силу свойства аддитивности момент инерции системы J складывается из моментов инерции втулки и спиц J0 и моментов инерции четырех грузов, то есть J=J0+J1+J2+J3+J4. Если грузы имеют форму цилиндров, и они расположены на одинаковом расстоянии l от оси вращения, тоJ1=J2=J3=J4.=Jц. Считая цилиндры материальными точками с массой (это допустимо, если длина цилиндра Ll), для момента инерции системы получаем J=J0+4l2. (1) Поскольку цилиндры имеют конечные размеры, то формула (1) верна лишь приближенно. Для получения точной формулы необходимо получить выражение для момента инерции прямого коаксиального цилиндра длиной L, имеющего внутренние и внешние радиусы r и R соответственно, центр масс которого расположен на расстоянии l от оси вращения Z, направленной перпендикулярно к оси цилиндра. Вначале следует получить выражение для момента инерции такого цилиндра относительно оси Z’, которая проходит через центр масс цилиндра параллельно оси вращения Z(см. рис.1). Вывод этого выражения базируется на формуле (19) введения. Процедура интегрирования по объему цилиндра подробно изложена в приложении к этой работе. В результате получается следующая формула для расчета Формулу для момента инерции цилиндра Jц относительно оси Z можно записать, используя теорему о параллельном переносе осей (формула (20) введения). Таким образом, чтобы определить момент инерции цилиндра относительно оси вращения Z, достаточно измерить его геометрические размеры и расстояние l от оси вращения до центра цилиндра. Измерение геометрических размеров цилиндра проводится штангенциркулем, а расстояние l с помощью линейки с миллиметровой шкалой. Итак, можно считать, что погрешности Сr=СR=СL и равны цене деления нониуса штангенциркуля, а Сlравна цене деления шкалы линейки. Масса указана на самих цилиндрах, а погрешность Сравна единице последнего знака указанного значения, т.е.1г. 2. Величину момента инерции одинаковых грузов, размещенных на одинаковых расстояниях от оси на спицах маятника Обербека, можно определить, если экспериментально определить момент инерции пустого (без грузов) маятника J0 и момент инерции нагруженного маятника J. Тогда разность этих величин даст суммарный момент инерции грузов, укрепленных на спицах. Этот способ применим для грузов произвольной формы, момент инерции которых невозможно рассчитать. Для экспериментального определения значения момента инерции системы, состоящей из маятника Обербека и укрепленных на нем грузов, надо измерить угловое ускорение системы в зависимости от момента внешних сил. Эта связь, согласно формулам (17) и (19) введения, должна быть линейной с коэффициентом пропорциональности равным моменту инерции системы J. Момент силы натяжения Т, которая является внешней по отношению к рассматриваемой системе, равен M=R0T, так как угол между направлением действия силы Т и радиус-вектором точки приложения этой силы равен /2. Для определения Т запишем уравнение движения гири массой m (формула (2) введения). ma = mg – T, (4)где а – ускорение падающей гири. Отсюда T=m(g-a), а момент силы натяжения есть M=mR0(g-a). (5) Под действием этого момента силы система будет вращаться с возрастающей угловой скоростью, величину которой можно легко найти, применяя формулу (4) введения к точке приложения силы, находящейся на расстоянии R0 от оси вращения. Линейная скорость точки приложения силы v=R0. Линейное ускорение этой точки a=dv/dt есть не что иное, как ускорение гири. Таким образом, a=dv/dt=R0(d/dt). Но (d/dt)= есть угловое ускорение системы. Тогда = d/dt = a/R0. (6) Из соотношений (5) и (6) видно, что для определения М и достаточно найти ускорение падающей гири, что можно сделать по формуле для перемещения при равноускоренном движении a=2h/t2, где h – расстояние, которое груз прошел за время падения t. Таким образом, выражения для определения М и приобретают следующий вид Таким образом, измеряя время опускания t на определенное расстояние h при различных массах гирь m, можно, используя формулы (7) и (8), получить экспериментальную зависимость M от . Теоретическая зависимостьM от определяется формулой (17) введения. Если учесть, что суммарный момент внешних сил включает в себя и момент сил трения (MТ), то уравнение моментов примет следующий вид: M=MТ+J. (9) Уравнение (9) – уравнение прямой, которая отсекает на оси Y отрезок, равный MТ и имеет тангенс угла наклона к оси X, равный J. Численные значенияMТ и J можно определить по экспериментальной зависимости М от методом наименьших квадратов, о котором подробно будет идти речь ниже. В формулах (7) и (8) величины R0, m, h и tесть результаты прямых измерений, которые в данной лабораторной работе проводятся на установке, представляющей собой собранные на массивном основании колонки для крепления маятника Обербека и миллисекундомера. На колонке размещены два кронштейна с фотодатчиками (нижний кронштейн неподвижен, верхний может перемещаться вдоль колонки). На корпусе кронштейнов имеются отметки, расстояние между которыми можно отсчитать по миллиметровой шкале, нанесенной на колонке. Это расстояние есть не что иное, как величина h. Погрешность определения высоты падения h=1мм. В верхней части колонки закреплен блок, через который перекинута нить. К одному концу прикрепляются гири, на которых указана их масса. Погрешность определения массы m=0,1г. Другой конец нити наматывается на диск, жестко скрепленный с крестовиной маятника Обербека. Диаметр диска, равный 2R0,измеряется штангенциркулем. Вся система может удерживаться в покое при помощи электромагнита и фрикционной муфты. На лицевой стороне панели миллисекундомера расположены: -клавиша сеть - включатель сети. При нажатии этой клавиши на световом табло должны высвечиваться нули и должны гореть лампочки фотодатчиков. -клавиша сброс - сброс показаний секундомера. Нажатие этой клавиши вызывает обнуление схем секундомера. -клавиша пуск - управление электромагнитом. Нажатие ее вызывает освобождение электромагнита и генерирование импульса, разрешающего измерение. Установка включается клавишей сеть. Гиря устанавливается так, чтобы нижний его край совпадал с чертой на корпусе верхнего фотодатчика. При отжатой клавише пуск вся система фиксируется электромагнитом. Нажатие этой клавиши отключает питание электромагнита, и гиря начинает движение. В момент перекрывания светового потока, падающего на фоторезистор верхнего фотодатчика, генерируется электрический импульс, который подключает к счетчику времени кварцевый генератор. Счетчик подсчитывает число импульсов, следующих с кварцевого генератора с частотой 10 кГц. Счет продолжается до тех пор, пока при своем движении нижний край гири не перекроет световой поток нижнего фотодатчика. В этот момент генерируется импульс, отключающий счетчик от кварцевого генератора и включат питание электромагнита. Относительная погрешность измерения времени составляет 0,02%. ВЫПОЛНЕНИЕ РАБОТЫ И УСЛОВИЯ ЭКСПЕРИМЕНТАСнять цилиндры со спиц маятника Обербека. Штангенциркулем измерить их геометрические размеры. Отрегулировать установку так, чтобы колонка была вертикальна. Верхний кронштейн установить на выбранную высоту так, чтобы гири, падая, проходили через середину рабочих окон фотодатчика. По шкале, расположенной на колонке, отсчитать значение h. Измерить штангенциркулем диаметр диска (2R0), на который наматывается нить. Оценить момент сил трения МТ. Для этого необходимо подобрать такой максимальную массу гири m0, при которой маятник еще неподвижен. Очевидно, что в этом случае MT=m0gR0. Определить экспериментальную зависимость углового ускорения от момента внешних сил М для пустого маятника. Для этого надо измерить время t, за которое гиря массой mопускается на высоту h. Это измерение надо проводить при различных массах гирь, причем при каждом значении m измерение t провести 3 раза. Результаты измерений представить в виде таблицы:
В этой таблице значения и М рассчитываются по формулам (7) и (8). Оценить случайные и систематические составляющие погрешностей и М. Построить экспериментальные точки в координатной плоскости X=и Y=M. Проведя по этим точкам наилучшую прямую, оценить величины момента инерции и момента сил трения для пустого маятника. Окончательную обработку этой зависимости провести, используя метод наименьших квадратов.Разместить цилиндры на минимальном расстоянии. Измерить это расстояние.(lmin). Рассчитать величину момента инерции цилиндра в этом случае Разместить цилиндры на максимальном расстоянии. Измерить это расстояние.(lmax). Рассчитать величину момента инерции цилиндра в этом случае ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТАДля того чтобы корректно сравнить величины моментов инерции цилиндра, полученные по теоретической формуле (3) и методом наименьших квадратов при обработке экспериментальных зависимостей от М, необходимо рассчитать погрешности определения этих величин. Значения моментов инерции 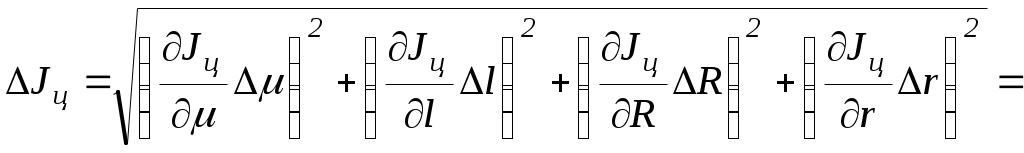 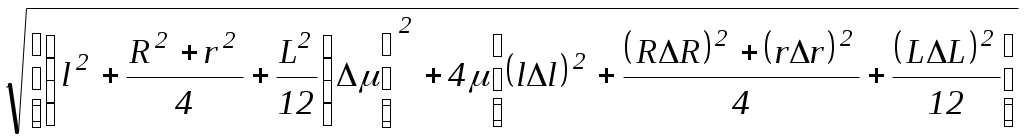 . (10) . (10)Здесь , l, R, rи L – систематические погрешности измерения этих величин. Прежде чем приступить к построению экспериментальных точек, необходимо оценить погрешности определения величин и М, которые рассчитываются по формулам (7) и (8). Измерение и М есть измерения косвенные. Тогда, пренебрегая погрешностью g по сравнению с погрешностями других величин, получаем 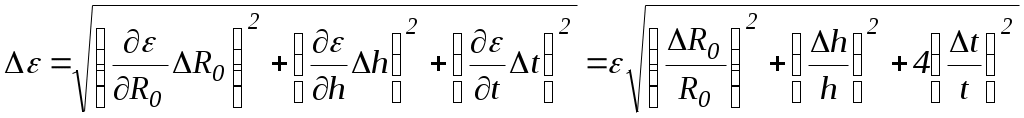 , (11) , (11)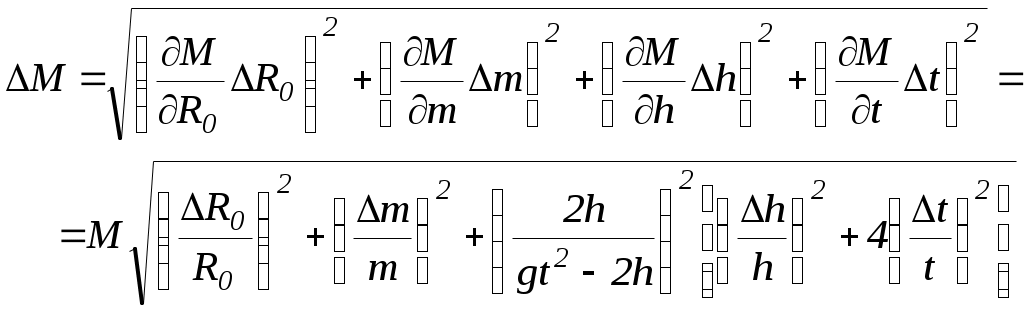 . (12) . (12)Подстановка в эти формулы систематических погрешностей прямых измерений величин R0, m, h и tпозволяет определить систематические составляющие погрешностей и М. При расчете случайных составляющих погрешности этих величин формулы (11) и (12) существенно упрощаются, так как учитывается лишь случайная погрешность измерения времени, то есть 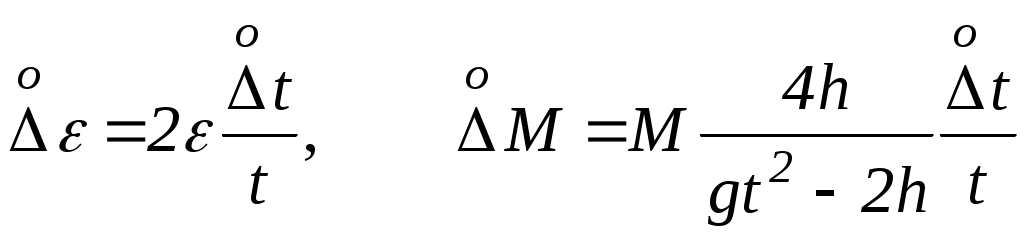 Поскольку необходимо лишь оценить величины погрешностей, достаточно рассчитать только максимальные значения М и . Приближенно величины параметров Jи МТ можно определить графическим способом. Для этого необходимо на миллиметровой бумаге изобразить координатные оси. По оси абсцисс будем в определенном масштабе откладывать величину , а по оси ординат – величину М. В этих координатных осях следует построить экспериментальные точки (i, Mi). Согласно формуле (9), зависимость М от линейна. Тогда, проведя по экспериментальным точкам наилучшую прямую, можно найти тангенс угла наклона этой прямой, который равен, очевидно, J. Отсекаемая наилучшей прямой на оси ординат часть будет равна МТ. В первом приближении наилучшей прямой можно считать такую прямую, относительно которой экспериментальные точки расположены симметрично по обе стороны от нее. (Нечто похожее приведено на рис.2.). Такую прямую можно провести, используя прозрачную линейку. Более строго понятие наилучшей прямой определяется в методе наименьших к 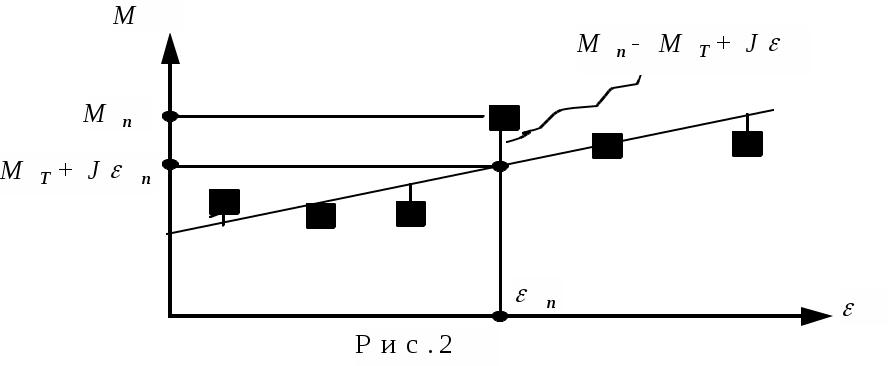 вадратов. вадратов.
Выберем за меру отклонения функции от экспериментальных данных для n-го опыта величину (Mn-MТ -J n)2 (рис.2). Почему именно эта величина, а не просто Mn-MТ -J n? Ясно, что оба уклонения MТ +J n от Мn нехороши: плохо, если J и МТ таковы, что Mn<MТ -J n, но также нехорошо, если A таково, что Mn>MТ -J n. Если бы за меру отклонения мы взяли Mn-MТ -J n, а затем стали бы находить сумму отклонений в нескольких опытах, то мы могли бы получить весьма малую величину за счет взаимного уничтожения отдельных слагаемых большой величины, но разных знаков. Это, однако, вовсе не говорило бы, что взятая функция М=МТ+Jхороша. Если за меру отклонения взять величину (Mn-MТ -J n)2, то такого взаимного уничтожения не будет, так как все величины величину (Mn-MТ -J n)2>0. Итак, в качестве меры общего отклонения S0 в описании экспериментальных данных функцией М=МТ+Jнеобходимо взять сумму мер отклонений для всех опытов, то есть Таким образом, функция М=МТ+J будет наилучшим образом соответствовать опытным данным, если S0, то есть сумма квадратов отдельных отклонений, минимальна. Метод определения констант, входящих в формулу, из требования минимальности S0, называется методом наименьших квадратов. Величина S0 является функцией от J и МТ, то есть S0=S0(J, МТ). Надо выбрать числа J и MT так, чтобы величина S0 была наименьшей. Для этого поступим так. Если бы MT было уже найдено, то S0 зависело бы только от J, то есть S0=S0(J). Поэтому величина S0 была бы наименьшей при таком J,при котором dS0/dJ=0. То есть должно было бы быть С другой стороны, если бы уже было найдено J, то должно было бы быть Эти условия дают следующую систему уравнений для определения величин J и MT: 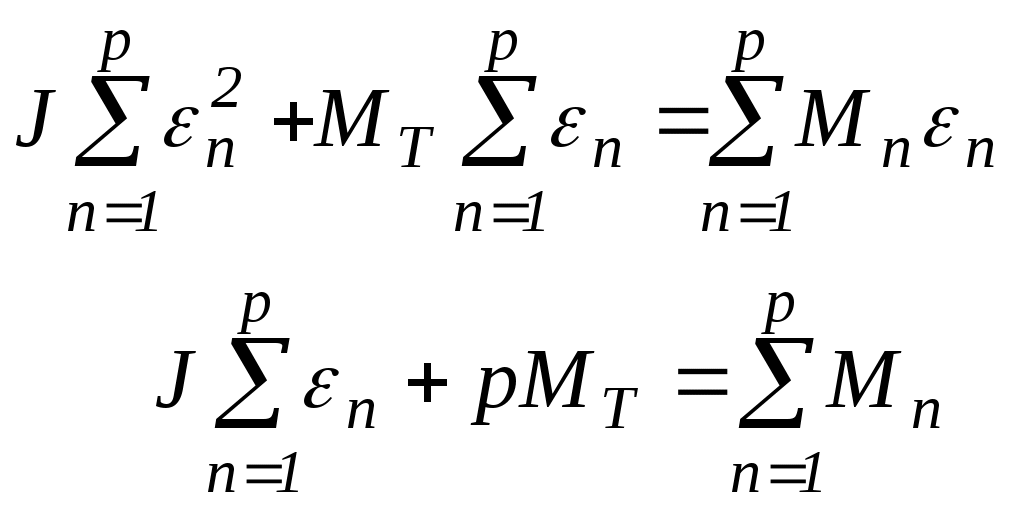 или или Здесь введены обозначения: Решая систему (14), получимЗная J и MT, можно рассчитать среднеквадратичное отклонение S, которое характеризует среднюю степень отклонения экспериментальных результатов от прямой М=МТ+J. 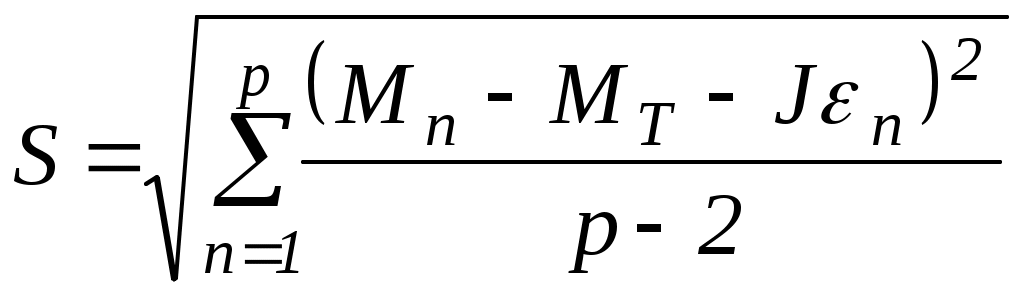 . (16) . (16)Среднеквадратичные отклонения величин J и MTопределяются по следующим формулам: 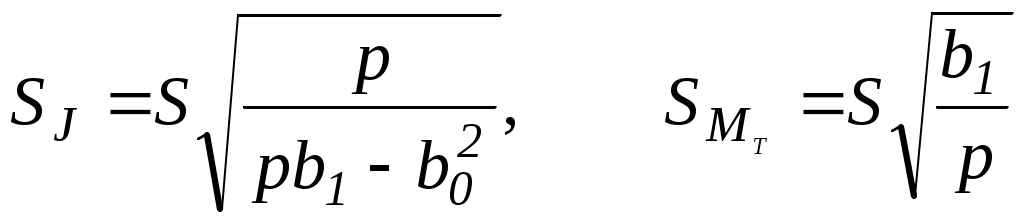 . (17) . (17)Наконец, доверительные интервалы для J и MTпри выбранной доверительной вероятности рассчитываются таким образом то есть коэффициент Стъюдента выбирается по таблице для эффективной вероятности (1+)/2 и для числа точек на два меньшего, чем при обработке. Например, если надо найти доверительные интервалы при выбранной доверительной вероятности =0,90 для параметров J и MT, полученных при обработке 10 точек (p=10), то в формулу (18) должно подставляется значение коэффициента Стъюдента t0.95, 8. Итак, имеющиеся в распоряжении три экспериментальные зависимости М от следует обработать методом наименьших квадратов, применяя формулы (15) – (18). Используя полученные значения моментов инерции системы и моментов сил трения, надо построить наилучшие прямые и сравнить их с соответствующими экспериментальными зависимостями. Далее необходимо рассчитать величины Здесь J0 и J0 – значение момента инерции и погрешность этой величины для маятника без грузов. Подставляя в (19) вместо J и J значения момента инерции и его погрешности, рассчитанные по методу наименьших квадратов для маятника Обербека при максимальном расстоянии между грузами, получаем Теперь можно провести корректное сравнение полученных значений момента инерции со значениями ПРИЛОЖЕНИЕ 1Вычислим момент инерции цилиндра длиной L и радиусом R относительно оси Z, проходящей через центр масс перпендикулярно оси цилиндра (рис.3). С |